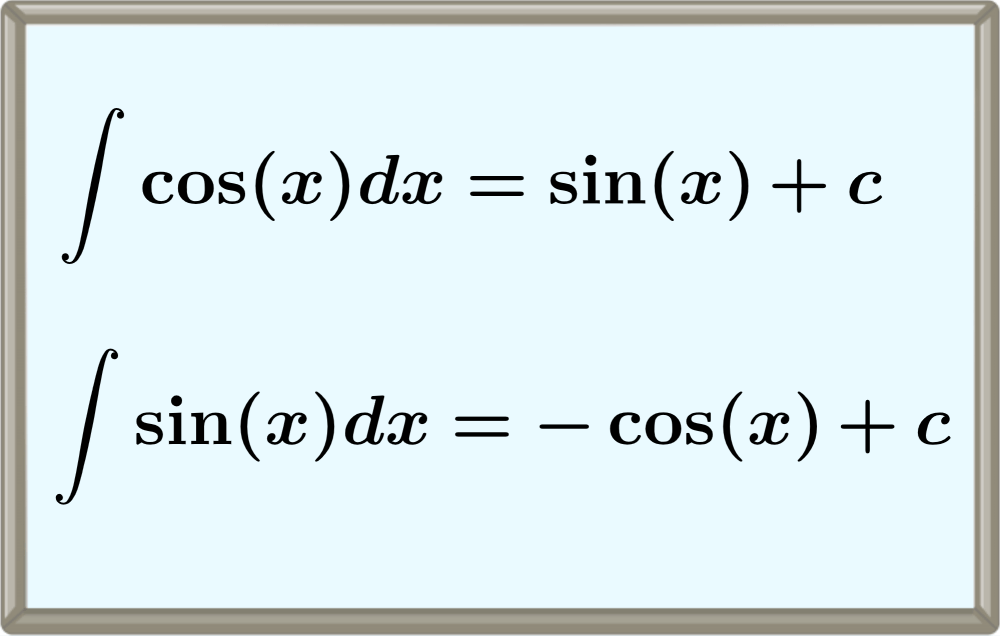Las integrales de funciones trigonométricas son otras funciones trigonométricas. Por ejemplo, la integral de la función coseno es igual a la función seno y la integral de la función seno es igual a coseno negativo.
A continuación, conoceremos las fórmulas más importantes de las integrales de las funciones trigonométricas. Luego, aplicaremos estas fórmulas para resolver algunos ejercicios prácticos.
Fórmulas de las integrales de funciones trigonométricas
Integral de la función seno
La integral de la función seno estándar es:
$$\int \sin(x) dx=-\cos(x)+c$$
La integral de la función seno de un ángulo de la forma $latex nx$ es:
$$\int \sin(nx) dx=-\frac{1}{n}\cos(nx)+c$$
Podemos integrar composiciones de la función seno, como $latex \sin(2x)$ o $latex \sin^2(x)$ usando la regla de la cadena para integrales.
Integral de la función coseno
La integral de la función coseno estándar es:
$$\int \cos(x) dx=\sin(x)+c$$
La integral de la función coseno de un ángulo de la forma $latex nx$ es:
$$\int \cos(nx) dx=\frac{1}{n}\sin(nx)+c$$
Integral de la función tangente
La integral de la función tangente estándar es:
$$\int \tan(x) dx=\ln| \sec(x)|+c$$
La integral de la función tangente multiplicada por la secante es:
$$\int \sec(x) \tan(x) dx=\sec(x)+c$$
Integral de la función cosecante
La integral de la función cosecante estándar es:
$$\int \cosec(x) dx=\ln\left| \tan\left(\frac{x}{2} \right)\right| +c$$
La integral de la función cosecante al cuadrado:
$$\int \cosec^2(x) dx=-\cot(x) +c$$
Integral de la función secante
La integral de la función secante estándar es:
$$\int \sec(x) dx=\ln| \tan(x)+\sec(x)| +c$$
La integral de la función secante al cuadrado es:
$$\int \sec^2(x) dx=\tan(x) +c$$
Integral de la función cotangente
La integral de la función cotangente estándar es:
$$\int \cot(x)dx=\ln|\sin(x)|+c$$
La integral de la función cotangente multiplicada por la cosecante es:
$$\int \cosec(x) \cot(x)dx=-\cosec(x)+c$$
Ejercicios resueltos de integrales de funciones trigonométricas
EJERCICIO 1
Resuelve la siguiente integral:
$$ \int \sin(4x) dx$$
Solución
Podemos usar la regla de la cadena de integrales para resolver esta integral.
Entonces, sabemos que la integral de $latex \sin(x)$ es igual a $latex -\cos(x)$. Además, observamos que la derivada de $latex 4x $ es 4, por lo que tenemos:
$$ \int \sin(4x) dx=-\frac{1}{4}\cos(4x)+c$$
EJERCICIO 2
Resuelve la siguiente integral:
$$ \int \sin(x) \cos(x)dx$$
Solución
Para resolver esta integral, podemos usar la siguiente identidad trigonométrica:
$$\sin(2x) \equiv 2 \sin(x) \cos(x)$$
$$\sin(x)\cos(x) \equiv \frac{1}{2}\sin(2x)$$
Entonces, tenemos:
$$ \int \sin(x) \cos(x)dx =\int \frac{1}{2}\sin(2x) dx$$
$$=\frac{1}{2}\left(-\frac{1}{2} \cos(2x)\right)+c$$
$$=-\frac{1}{4}\cos(2x)+c$$
EJERCICIO 3
Encuentra la siguiente integral:
$$ \int x^2 \cos(x^3-2)dx$$
Solución
Podemos resolver esta integral al observar que la derivada de $latex x^3-2$ es $latex 3x^2$ y que tenemos un término $latex x^2$ fuera de la función principal.
Entonces, usamos la regla de la cadena para integrales y tenemos:
$$ \int x^2 \cos(x^3-2)dx=\frac{1}{3}\sin(x^3-2)+c$$
EJERCICIO 4
Encuentra la siguiente integral:
$$ \int \cos(x) \sin^2(x)dx$$
Solución
Esta integral es encontrada al observar que la derivada de $latex \sin(x)$ es $latex \cos$ y que la función $latex \cos(x)$ está afuera de la función principal.
Entonces, tenemos:
$$ \int \cos(x) \sin^2(x)dx =\frac{(\sin(x))^3}{3}+c$$
$$ =\frac{\sin^3(x)}{3}+c$$
EJERCICIO 5
Encuentra la siguiente integral:
$$ \int 2\sec(3x) \tan(3x)dx$$
Solución
Para resolver esta integral, vamos a usar la fórmula $latex \int \sec(x) \tan(x) dx=\sec(x)+c$.
Además, observamos que la derivada de $latex 3x$ es 3. Entonces, tenemos:
$$ \int 2\sec(3x) \tan(3x)dx=\frac{2}{3}\sec(3x)+c$$
EJERCICIO 6
¿Cuál es el resultado de la siguiente integral?
$$ \int x\sec^2(1-x^2) dx$$
Solución
Vamos a usar la integral $$\int \sec^2(x) dx=\tan(x) +c$$ para resolver este ejercicio.
Entonces, observamos que la derivada de $latex (1-x^2)$ es $latex -2x$ y tenemos un término $latex x$ fuera de la función principal. Entonces, tenemos:
$$ \int x\sec^2(1-x^2) dx=\frac{\tan(1-x^2)}{2}+c$$
Integrales de funciones trigonométricas – Ejercicios para resolver
Encuentra la integral $latex \int 12\cosec(4x)\cot(4x) dx$
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre integrales? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
