La hipotenusa de un triángulo rectángulo es el lado opuesto al ángulo de 90 grados. Podemos calcular la hipotenusa al usar el teorema de Pitágoras. Este teorema nos dice que la hipotenusa al cuadrado es igual a la suma de los cuadrados de las longitudes de los otros dos lados del triángulo. Entonces, para obtener la longitud de la hipotenusa, necesitamos tener las longitudes de los otros lados.
A continuación, haremos una revisión del teorema de Pitágoras. Además, usaremos a este teorema para resolver algunos ejercicios y encontrar la longitud de la hipotenusa.
GEOMETRÍA
Relevante para…
Aprender a encontrar la hipotenusa de un triángulo rectángulo.
GEOMETRÍA
Relevante para…
Aprender a encontrar la hipotenusa de un triángulo rectángulo.
¿Cómo hallar la hipotenusa de un triángulo rectángulo?
Para encontrar la hipotenusa de un triángulo rectángulo, usamos el teorema de Pitágoras. Recordemos que el teorema de Pitágoras nos dice que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los otros dos lados.
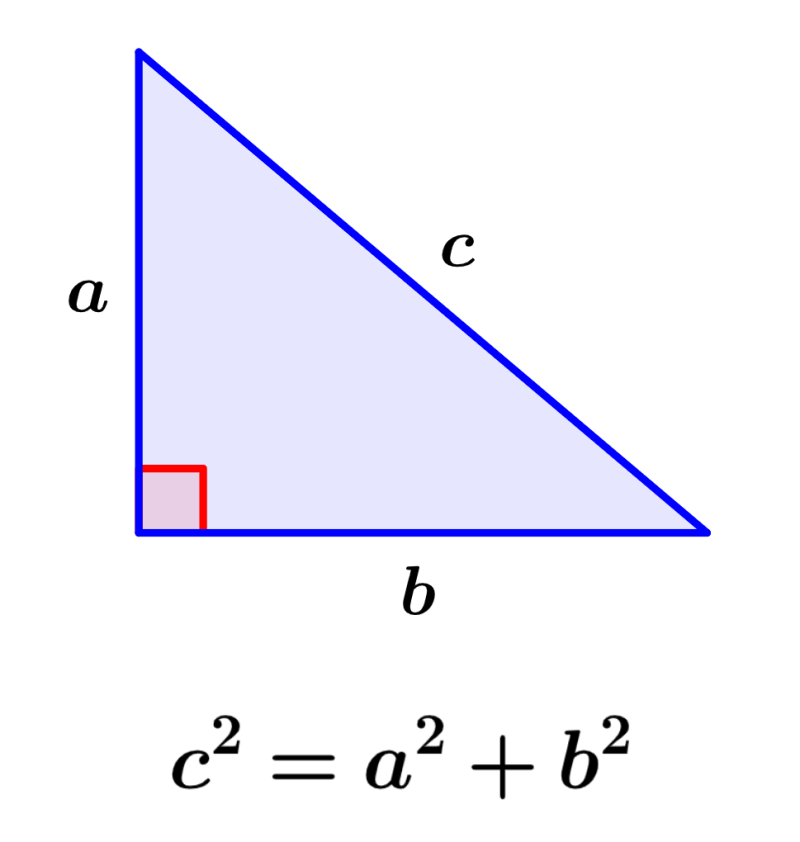
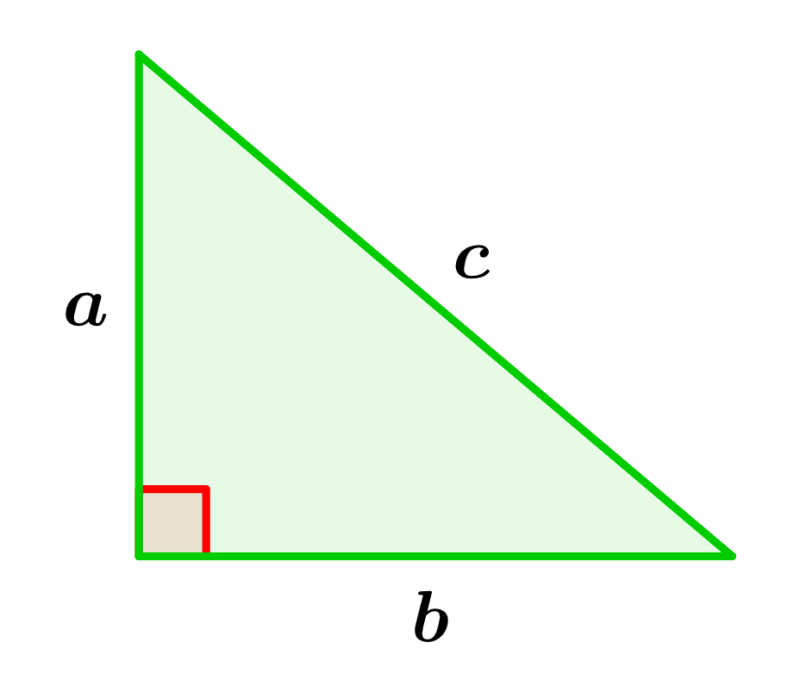
Por ejemplo, observemos la siguiente figura de un triángulo rectángulo:
En este triángulo, c es la hipotenusa, ya que es el lado opuesto al ángulo recto. Entonces, el teorema de Pitágoras nos dice:
| $latex {{c}^2}={{a}^2}+{{b}^2}$ |
en donde, c es la longitud de la hipotenusa y a y b son las longitudes de los otros dos lados.
Ejercicios de hipotenusa de triángulos rectángulos resueltos
La fórmula del teorema de Pitágoras es usada para resolver los siguientes ejercicios. Cada ejercicio tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo para practicar.
EJERCICIO 1
¿Cuál es la longitud de la hipotenusa de un triángulo rectángulo que tiene lados de longitud 3 m y 4 m?
Solución
Podemos reconocer que tenemos los lados $latex a=3$ y $latex b=4$. Entonces, usamos el teorema de Pitágoras con estos valores:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{3}^2}+{{4}^2}$
$latex {{c}^2}=9+16$
$latex {{c}^2}=25$
$latex c=5$
La longitud de la hipotenusa es 5 m.
EJERCICIO 2
Tenemos un triángulo rectángulo con lados de longitud 5 m y 12 m. ¿Cuál es su hipotenusa?
Solución
Tenemos las longitudes de los lados $latex a=5$ y $latex b=12$. Entonces, reemplazamos estos valores en el teorema de Pitágoras:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{5}^2}+{{12}^2}$
$latex {{c}^2}=25+144$
$latex {{c}^2}=169$
$latex c=13$
La longitud de la hipotenusa es 13 m.
EJERCICIO 3
¿Cuál es la hipotenusa de un triángulo rectángulo con lados de longitud 9 m y 12 m?
Solución
Tenemos las longitudes $latex a=9$ y $latex b=12$. Entonces, sustituimos estos valores en el teorema de Pitágoras:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{9}^2}+{{12}^2}$
$latex {{c}^2}=81+144$
$latex {{c}^2}=225$
$latex c=15$
La longitud de la hipotenusa es 15 m.
EJERCICIO 4
Tenemos un triángulo rectángulo con lados de longitud 10 m y 12 m. ¿Cuál es la longitud de su hipotenusa?
Solución
Aquí, tenemos las longitudes $latex a=10$ y $latex b=12$. Por lo tanto, usamos estos valores en el teorema de Pitágoras:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{10}^2}+{{12}^2}$
$latex {{c}^2}=100+144$
$latex {{c}^2}=244$
$latex c=15.62$
La longitud de la hipotenusa es 15.62 m.
EJERCICIO 5
¿Cuál es la longitud de la hipotenusa de un triángulo rectángulo que tiene lados de longitud 20 cm y 10 cm?
Solución
Podemos reconocer que tenemos los lados $latex a=20$ y $latex b=10$. Entonces, usamos el teorema de Pitágoras con estos valores:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{20}^2}+{{10}^2}$
$latex {{c}^2}=400+100$
$latex {{c}^2}=500$
$latex c=22.36$
La longitud de la hipotenusa es 22.36 cm.
Ejercicios de hipotenusa de triángulos rectángulos para resolver
Pon en práctica lo aprendido sobre el teorema de Pitágoras para encontrar la longitud de la hipotenusa de los triángulos rectángulos. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre triángulos rectángulos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
