Funciones Definidas por Partes o Funciones Definidas a Trozos

¿Qué es una función por partes o a trozos?

Las funciones por partes o también conocidas como funciones definidas a trozos son funciones que son definidas por diferentes fórmulas o funciones para cada intervalo. Como su nombre lo indica, estas funciones están definidas por trozos de funciones para cada parte del dominio.

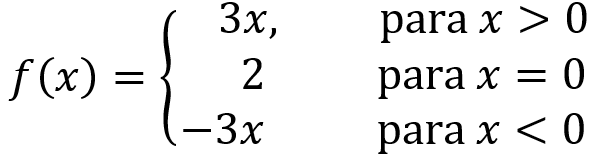
En la función de arriba, podemos ver que f(x) es una función definida por partes, ya que está definida de forma diferente para los tres intervalos x>0, x=0 y x<0.

Podemos interpretar a las funciones definidas por partes al mirar a los diferentes intervalos dados. La función f(x) dada arriba puede ser leída como:

• Cuando x>0, f(x) es igual a 3x.
• Cuando x=0, f(x) es igual a 2,
• Cuando x<0, f(x) es igual a -3x.

Estos cambios pueden ser observados claramente en la gráfica de la función:

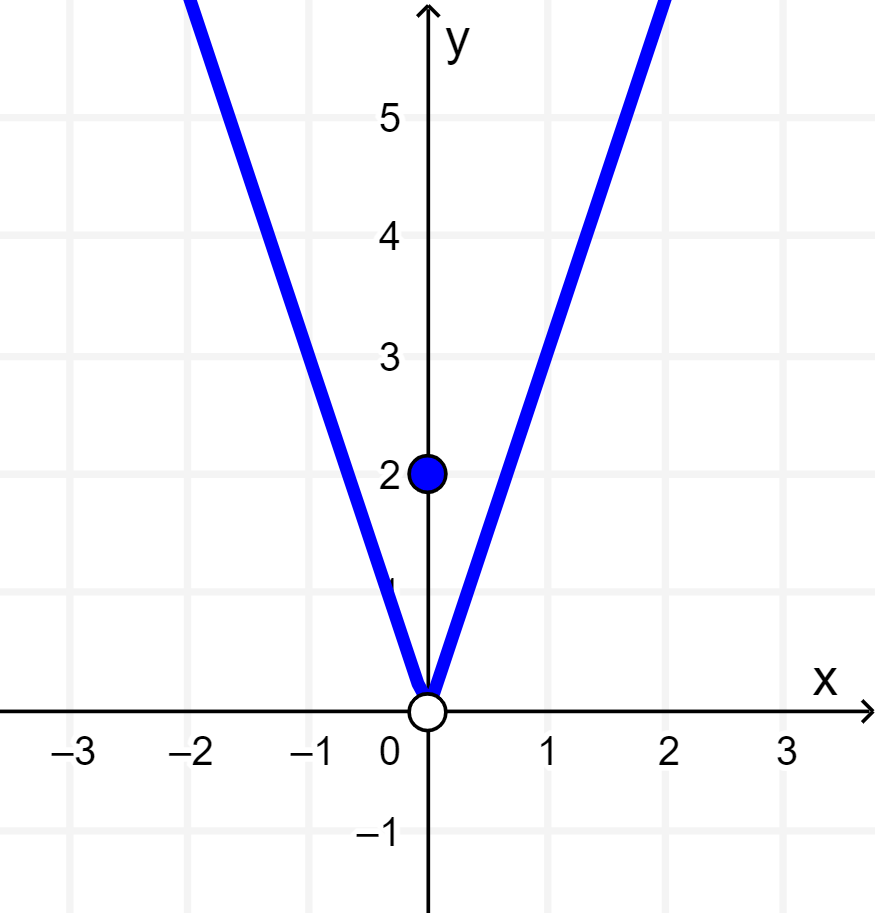
¿Cómo resolver funciones definidas a trozos?

Ahora que hemos aprendido un poco sobre estas funciones, tenemos que aprender cómo resolver funciones definidas a trozos.

Para resolver funciones definidas a trozos, debemos tomar en cuenta lo siguiente:

• Verifica cuidadosamente en dónde se ubica la x en el intervalo dado.
• Evalúa el valor usando la función correspondiente.

Por ejemplo, digamos que queremos encontrar f(5) en la siguiente función:

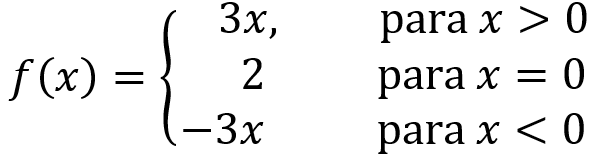
Dado que 5 es mayor que 0, la función que usaremos para evaluar f(5) es f(x) = 3x. Entonces, tenemos f(5) = 3(5) = 15.

Esto también significa que tenemos f(0) = 2 y también f(-1) = -3(-1)=3.

¿Cómo graficar funciones definidas a trozos?

Para graficar funciones definidas a trozos, debemos considerar que cada intervalo tendrá una gráfica diferente, ya que la función es diferente en cada intervalo.

Podemos tener en cuenta las siguientes recomendaciones al momento de graficar funciones definidas a trozos:

• Podemos pensar en cómo se verá cada función individualmente.
• Para intervalos inclusivos (como x≥0), incluimos los puntos finales usando puntos rellenos.
• Para intervalos exclusivos (como x>0), excluimos los puntos finales con puntos vacíos.

Algunas de las funciones más comunes que podemos esperar son las siguientes:

• Funciones constantes como f(x)=4.
• Funciones lineales como f(x)=3x+1.
• Funciones cuadráticas como f(x)=2x²+x-3.

Puedes explorar más tipos de funciones y sus gráficas en nuestro artículo sobre tipos de funciones. Esto te ayudará a tener una idea de cómo podemos esperar que se vea cada gráfica individual.

Ahora, grafiquemos la siguiente función como ejemplo:

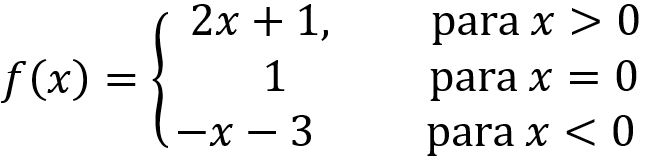
Cuando tenemos x>0, y x<0, la función retorna una expresión lineal. Podemos graficar estas partes lineales simplemente usando dos puntos que satisfagan estas expresiones y trazando una línea a través de los puntos teniendo en cuenta que f(x)=2x+1 solo corresponde a valores de x mayores que 0 y que f(x)=-x-3, solo corresponde a valores de x menores que 0. Dado que ambas son desigualdades exclusivas, tenemos un punto vacío en sus puntos finales:

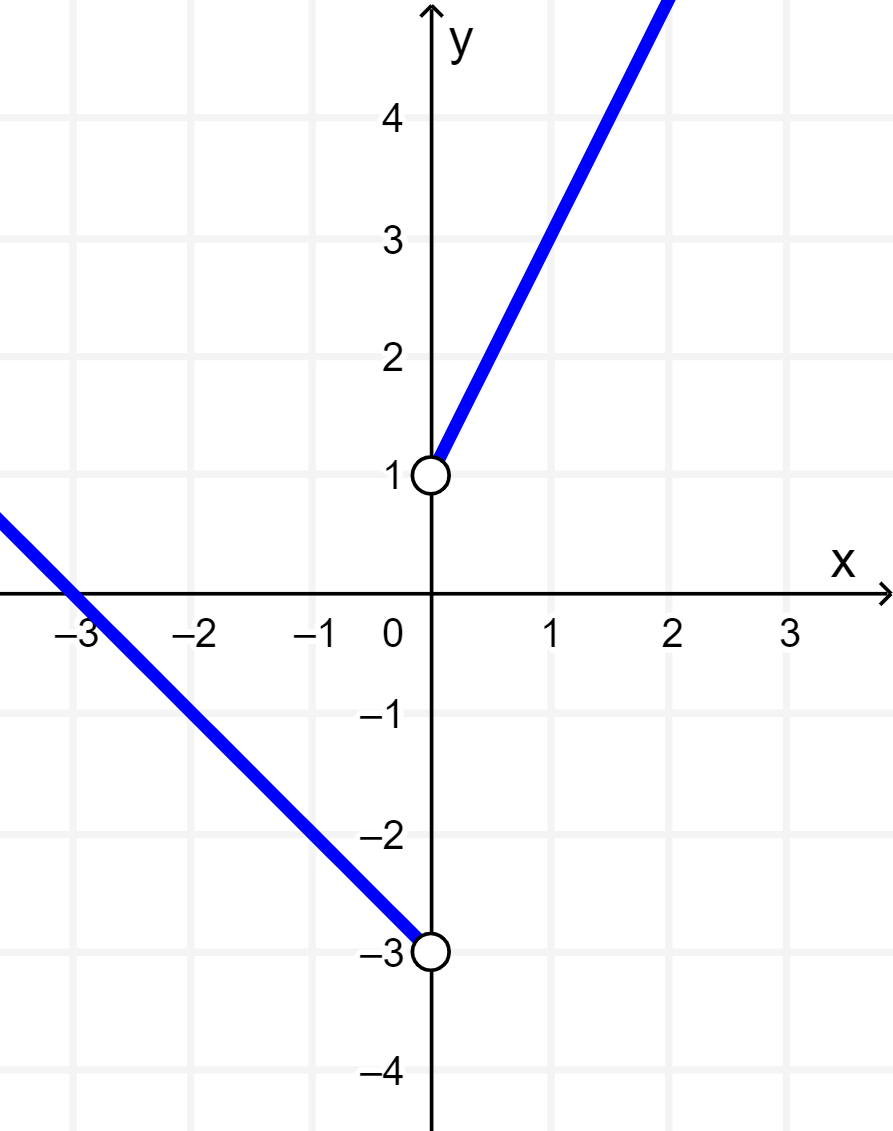
Ahora solo tenemos que completar la condición cuando x=0. Dado que el valor es constante en f(x)=1, podemos graficar el punto (0, 1):

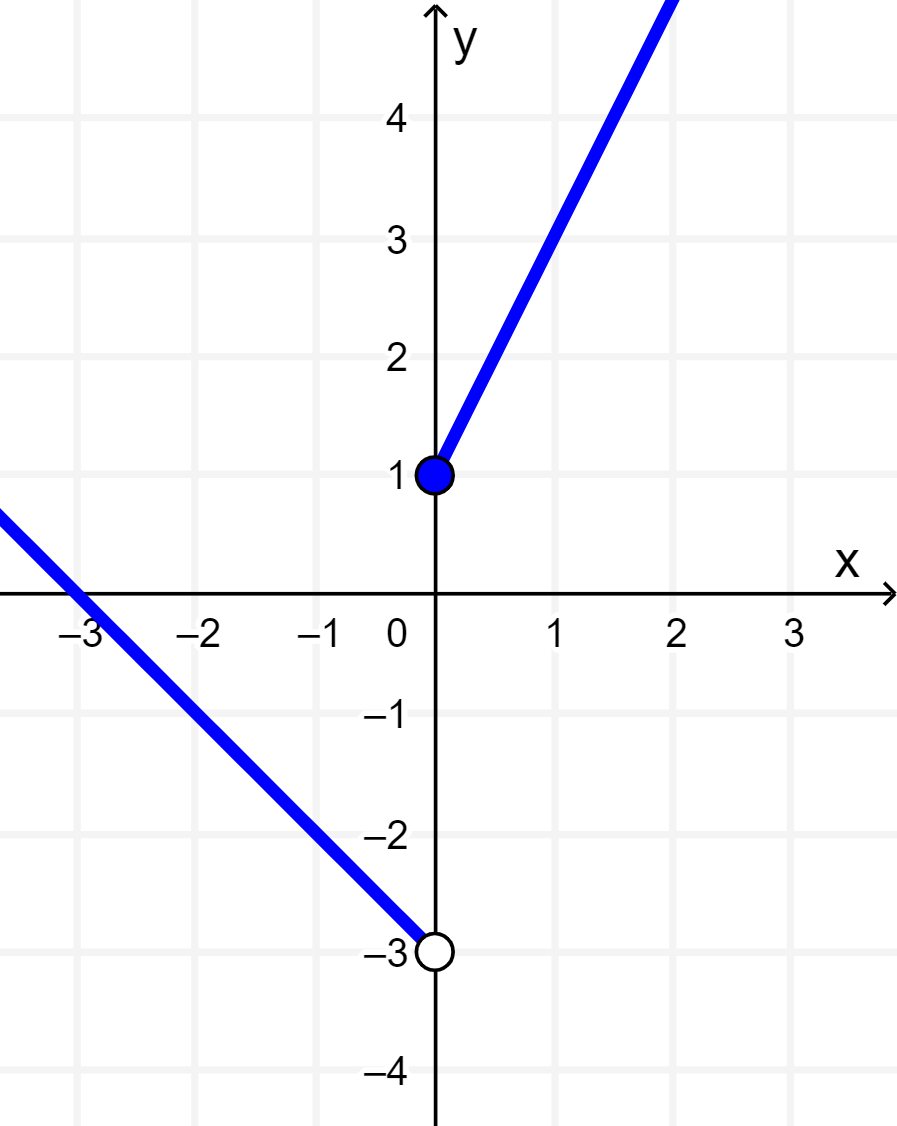
Esta es la gráfica final de esta función definida a trozos. En la gráfica, podemos ver que la función tiene un dominio de (-∞, ∞) y un rango de (-3, ∞).

Véase también

¿Interesado en aprender más sobre funciones? Mira estas páginas:

• Tipos de Funciones Algebraicas y sus Gráficas
• Notación de Funciones Ejemplos
• Dominio y Rango Ejemplos