La notación de funciones es la manera en la que una función es escrita. La notación de funciones es una manera precisa de dar información sobre la función sin la necesidad de tener largas explicaciones escritas.
En este artículo, aprenderemos un poco sobre las funciones y miraremos ejemplos de notación de funciones.
¿Qué es una función?
En matemáticas, una función es un conjunto de entradas con una sola salida en cada caso. Todas las funciones tienen un dominio y un rango. El dominio es el conjunto de valores independientes de la variable, para los cuales la función es definida. Es decir, el dominio es el conjunto de valores de x para los que existen valores reales de y.
Por otra parte, el rango es el conjunto de valores dependientes de la variable, y. Tanto el rango como el dominio pueden ser expresados en notación de intervalos o usando desigualdades.
¿Qué es la notación de funciones?
La notación de funciones es una manera en la que una función puede ser representada usando símbolos y signos. La notación de funciones es una manera más simple de escribir funciones sin la necesidad de escribir explicaciones escritas extensas.
La notación de funciones que es usada más frecuentemente es $latex f(x)$, lo cual es leído como “f de x”. En este caso, la letra x ubicada dentro del paréntesis representa al dominio de la función y el símbolo entero $latex f(x)$ representa al rango de la función.
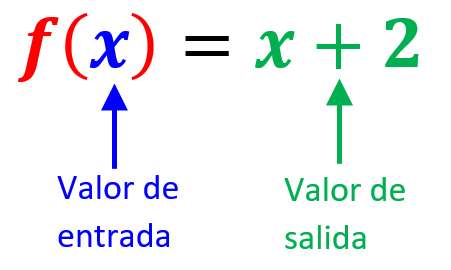
A pesar de que la f es la letra más usada, podemos usar cualquier otra letra del abecedario tanto minúscula como mayúscula. De igual forma, también podemos usar cualquier otra letra del abecedario en lugar de la x.
EJEMPLOS
Todas las siguientes son funciones:
- $latex f(x)=x-21$
- $latex h(x)={{x}^{2}}+2$
- $latex S(t)=3{{t}^{2}}-t+3$
- $latex juan(b)={{b}^{3}}-2b$
Ventajas de usar la notación de funciones
- Esta notación nos permite dar nombres individuales a las funciones y evitar confusiones al momento de evaluarlas. Por ejemplo, al tener $latex f(x)$ y $latex g(x)$, podemos distinguirlas fácilmente.
- La variable independiente puede ser identificada fácilmente. Por ejemplo, en la función $latex f(x)=2x+3$, sabemos que la variable es la x.
- Podemos determinar cuál elemento de la función debe ser examinado. Por ejemplo, encontrar $latex f(3)$ cuando $latex f(x)=4x-2$ es lo mismo que encontrar $latex y=4x-2$ cuando $latex x=3$.
Tipos de funciones
Hay varios tipos de funciones, pero las siguientes son las más comunes:
Funciones lineales
Una función lineal es un polinomio de primer grado. Una función lineal tiene la forma general $latex f(x)=ax+b$, en donde a y b son valores numéricos y a es diferente de cero.
Funciones cuadráticas
Una función cuadrática es una función polinómica de segundo grado. La forma general de una función cuadrática es $latex f(x)=a{{x}^{2}}+bx+c$, en donde a, b y c son valores numéricos y a es diferente de cero.
Función cúbica
La función cúbica es una función polinómica de tercer grado que tiene la forma general $latex f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+d$, en donde a, b, c y d son valores numéricos y a es diferente de cero.
Función trigonométrica
Las tres funciones trigonométricas fundamentales son $latex f(x)=\sin(x)$, $latex f(x)=\cos(x), f(x)=\tan(x)$.
Función exponencial
Una función exponencial es una función en la que la variable aparece como exponente. Tiene la forma general $latex f(x)={{b}^{x}}$.
Función logarítmica
Una función logarítmica es una función en la que la variable aparece como el argumento de un logaritmo. Tiene la forma general $latex {{\log }_{b}}x$, en donde b es la base del logaritmo.
Notación de funciones ejemplos
Podemos aplicar la notación de funciones para evaluar problemas matemáticos con mayor facilidad como se muestra en los ejemplos:
EJEMPLO 1
Dada la función $latex f(x)=3x-5$, encuentra el valor de $latex f(3)$.
Solución: Sustituimos el 3 en vez de la x en la función:
$latex f(x)=3x-5$
$latex f(3)=3(3)-5$
$latex f(3)=9-5$
$latex f(3)=4$
Esta respuesta puede ser pensada como el par ordenado (3, 4).
EJEMPLO 2
Encuentra el valor de la función $latex g(t)=2{{t}^{2}}-t+3$, cuando $latex t=-2$.
Solución: Sustituimos el 3 en vez de la x en la función:
$latex g(t)=2{{t}^{2}}-t+3$
$latex g(-2)=2{{(-2)}^{2}}-(-2)+3$
$latex g(t)=2(4)+2+3$
$latex g(t)=13$
Esta respuesta puede ser pensada como el par ordenado (-2, 13).
EJEMPLO 3
Encuentra $latex h(2s)$, para la función $latex h(x)=3x-16$.
Solución: Esto es similar a los problemas anteriores con la diferencia que ahora sustituimos variables:
$latex h(x)=3x-16$
$latex h(2s)=3(2s)-16$
$latex h(2s)=6s-16$
Ahora la función está en términos de s.
EJEMPLO 4
Dada la función $latex g(s)=3{{s}^{3}}+2s-10$, encuentra el valor de $latex g(3)$.
Solución: Sólo tenemos que sustituir el 3 en vez de la s en la función:
$latex g(s)=3{{s}^{3}}+2s-10$
$latex g(3)=3{{(3)}^{3}}+2(3)-10$
$latex g(3)=3(27)+6-10$
$latex g(3)=81+6-10$
$latex g(3)=77$
Podemos presentar esta respuesta como el par ordenado (3, 77).
EJEMPLO 5
Dada la función $latex f(x)=2{{x}^{2}}+x-5$, encuentra el valor de $latex f(m+1)$.
Solución: En vez de reemplazar un número, reemplazamos con $latex m+1$:
$latex f(x)=2{{x}^{2}}+x-5$
$$f(m+1)=2{{(m+1)}^{2}}+m+1-5$$
$$f(m+1)=2({{m}^{2}}+2m+1)+m-4$$
$$f(m+1)=2{{m}^{2}}+4m+2+m-1$$
$latex f(m+1)=2{{m}^{2}}+5m+1$
Ahora tenemos una función en términos de m.
Inténtalo tú mismo – Resuelve los siguientes ejercicios
Véase también
¿Interesado en aprender más sobre funciones? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
