El dominio es el conjunto de valores posibles para las entradas de la función, es decir, los valores de x. El rango es el conjunto de valores posibles para las salidas de la función, es decir, los valores de y. En este artículo, miraremos algunos ejemplos resueltos del dominio y rango de funciones.
ÁLGEBRA
Relevante para…
Aprender sobre el dominio y el rango de funciones con ejemplos.
ÁLGEBRA
Relevante para…
Aprender sobre el dominio y el rango de funciones con ejemplos.
Dominio
El dominio de la función es el conjunto de todos los valores posibles de la variable independiente. Es decir, el dominio es el valor de todos los valores de x que funcionarán y harán que la función retorne valores reales de y.
¿Cómo encontrar el dominio?
Podemos determinar el dominio de la función al buscar los valores de la variable independiente (usualmente la x), los cuales sí podemos usar en la función. Usualmente, esto implica evitar valores que producen un 0 en el denominador de fracciones o evitar tener valores negativos dentro de raíces cuadradas.
Entonces, para encontrar el dominio, lo importante es recordar que:
- El denominador de una fracción no puede ser cero.
- El número dentro de una raíz cuadrada debe ser positivo.
EJEMPLO
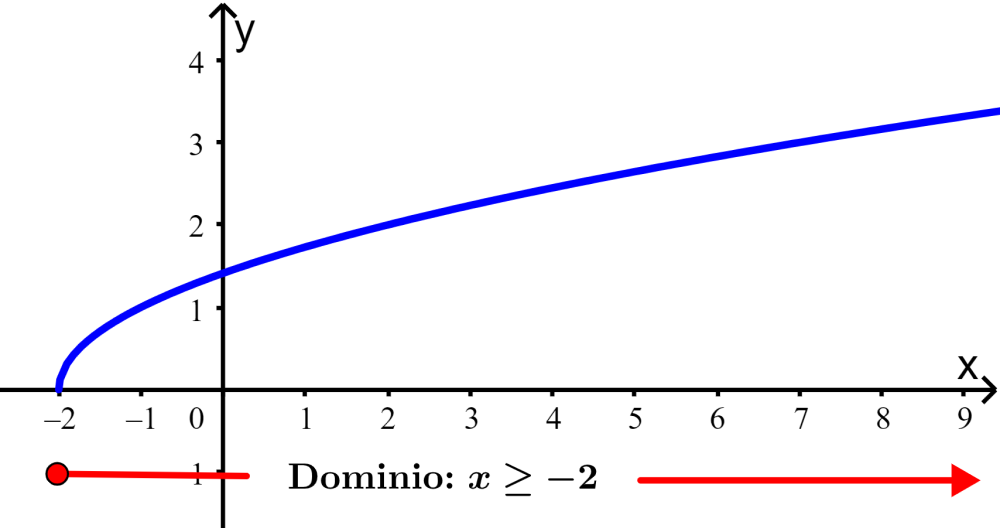
La siguiente es la gráfica de $latex y=\sqrt{{x+2}}$:
El dominio de esta función es $latex x\ge -2$, debido a que x no puede ser menor que -2. Para verificar esto, podemos intentar con el número -3. Reemplazando $latex x=-3$, tenemos $latex y=\sqrt{{-3+2}}=\sqrt{{-1}}$.
Tenemos un número negativo dentro de una raíz cuadrada y el resultado no es un número real, por lo que sólo valores de x mayores o iguales a -2 producen valores reales en la función.
Rango
El rango de la función es el conjunto de todos los valores posibles de la variable dependiente luego de haber sustituido el dominio. Es decir, el rango son los valores resultantes de y que obtenemos después de haber sustituido todos los posibles valores de x.
¿Cómo encontrar el rango?
Para encontrar el rango tenemos en cuenta lo siguiente:
- El rango de una función es el conjunto de valores de y desde el valor mínimo hasta el valor máximo.
- Podemos sustituir algunos valores de x para determinar lo que sucede con los valores de y. Podemos averiguar si es que los valores de y son siempre positivos, siempre negativos.
- Asegúrate de encontrar los valores mínimos y máximos de y.
- Traza una gráfica básica para visualizar el problema.
EJEMPLO
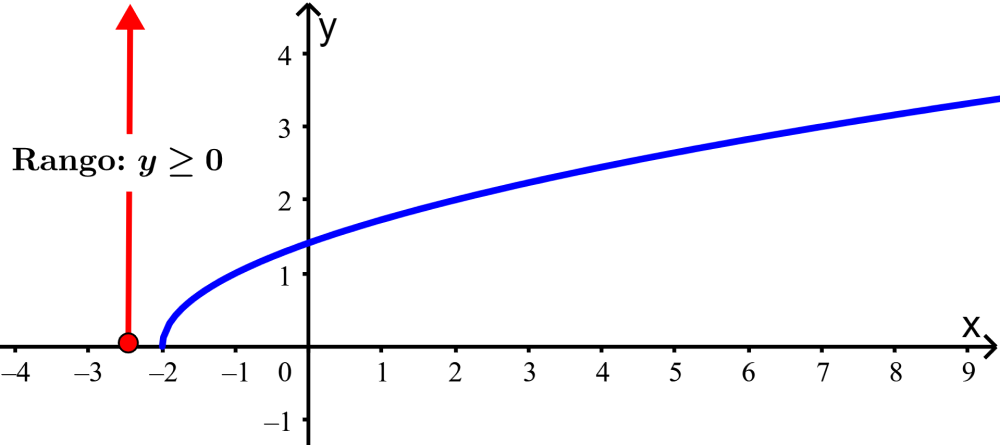
Nuevamente, miremos la gráfica de $latex y=\sqrt{{x+2}}$:
Podemos observar que la curva siempre está encima del eje horizontal. Sin importar el valor de x que intentemos, siempre obtendremos un valor de y que es cero o positivo. En este caso, el rango es $latex y\ge 0$.
La gráfica se va hacia la derecha indefinidamente, por lo que el rango es todos los valores no negativos de y.
¿Cómo encontrar el dominio y el rango sin usar una gráfica?
Siempre es más fácil determinar el dominio y el rango cuando tenemos una gráfica, siempre y cuando nos aseguremos de hacer acercamientos y alejamientos para capturar todos los detalles necesarios. Sin embargo, graficar una función no siempre es posible, ya que quizás no tengamos software o calculadoras para graficar en un cierto momento.
Para encontrar el dominio y el rango sin usar una gráfica, usamos lo que ya vimos anteriormente:
- No podemos tener valores negativos dentro de un signo de raíz cuadrada.
- No podemos tener ceros en el denominador de una fracción.
EJEMPLO
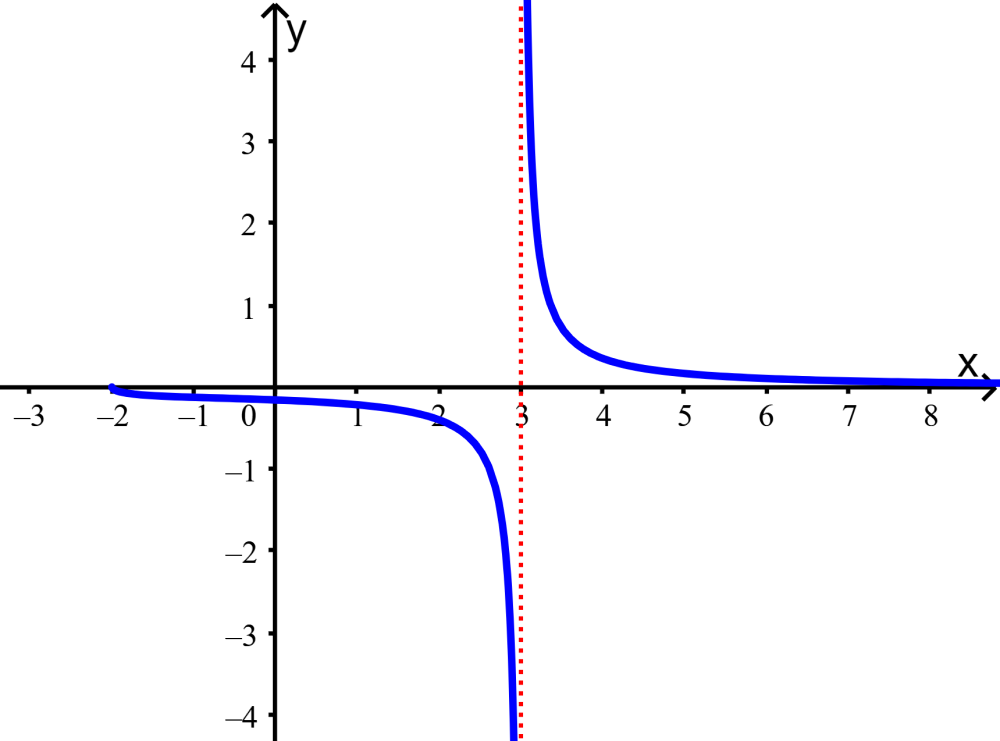
Encuentra el dominio y el rango de la función $latex f\left( x \right)=\frac{{\sqrt{{x+2}}}}{{{{x}^{2}}-9}}$ sin usar una gráfica.
Solución: En el numerador de la fracción, tenemos una raíz cuadrada. Para asegurarnos que el valor bajo la raíz no sea negativo, sólo podemos usar valores de x que sean mayores o iguales a -2.
El denominador de la fracción tiene $latex {{x}^{2}}-9$, lo cual podemos escribir como $latex (x+3)(x-3)$. Entonces, nuestros valores para x no pueden incluir -3 para el primer paréntesis y 3 para el segundo paréntesis.
Entonces, el dominio para esta función es $latex x\ge -2,~~x\ne 3$.
Para determinar el rango, consideramos al numerador y al denominador de la función separadamente:
Numerador: Si es que $latex x=-2$, tenemos $latex f\left( x \right)=\sqrt{{-2+2}}=0$. A medida que x incrementa, el numerador también incrementará hasta ir al infinito.
Denominador: Dividimos en las siguientes partes:
Cuando $latex x=-2$, la parte inferior de la función es igual a $latex {{(-2)}^{2}}-9=4-9=-5$. Entonces tenemos $latex f(-2)=\frac{0}{-5}=0$.
Entre $latex x=-2$ y $latex x=3$, la expresión $latex {{(x)}^{2}}-9$ se acerca a 0, por lo que la función tenderá a infinito a medida que nos acercamos a $latex x=3$.
Para $latex x>3$, cuando x es un poco más grande que 3, el valor del denominador es un poco más grande que 0, por lo que la función tendrá un valor muy grande positivo.
Para valores de x muy grandes, el numerador será grande, pero el denominador será mucho más grande, por lo que el valor de la función se hará cada vez más pequeño.
Entonces, el rango de la función es $latex \left( {-\infty ,~0} \right],~\left( {\infty ,~0} \right)$.
Podemos visualizar esto en la gráfica:
Dominio y rango ejemplos resueltos
EJEMPLO 1
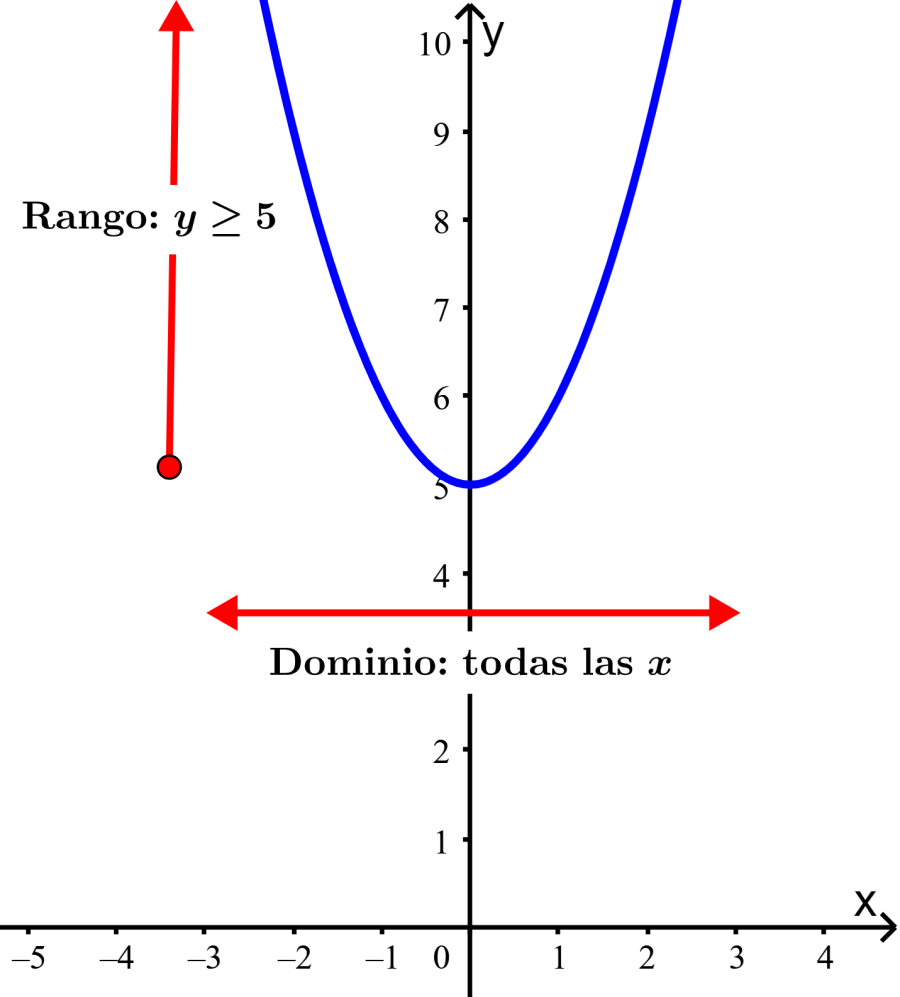
Encuentra el dominio y el rango para la función $latex f(x)={{x}^{2}}+5$.
Dominio: La función $latex f(x)={{x}^{2}}+5$ está definida para todos los valores de x ya que no hay ninguna restricción en el valor de x. Por lo tanto, el dominio de $latex f(x)$ es “todos los valores reales de x.
Rango: Debido a que $latex {{x}^{2}}$ nunca es negativo, la función $latex f(x)={{x}^{2}}+5$ nunca es menor que 5. Por lo tanto, el rango de $latex f(x)$ es “todos los números reales $latex f(x)\ge 5$.
En la gráfica podemos ver que el dominio es todos los números reales, pero el rango es todos los números reales mayores que 5:
EJEMPLO 2
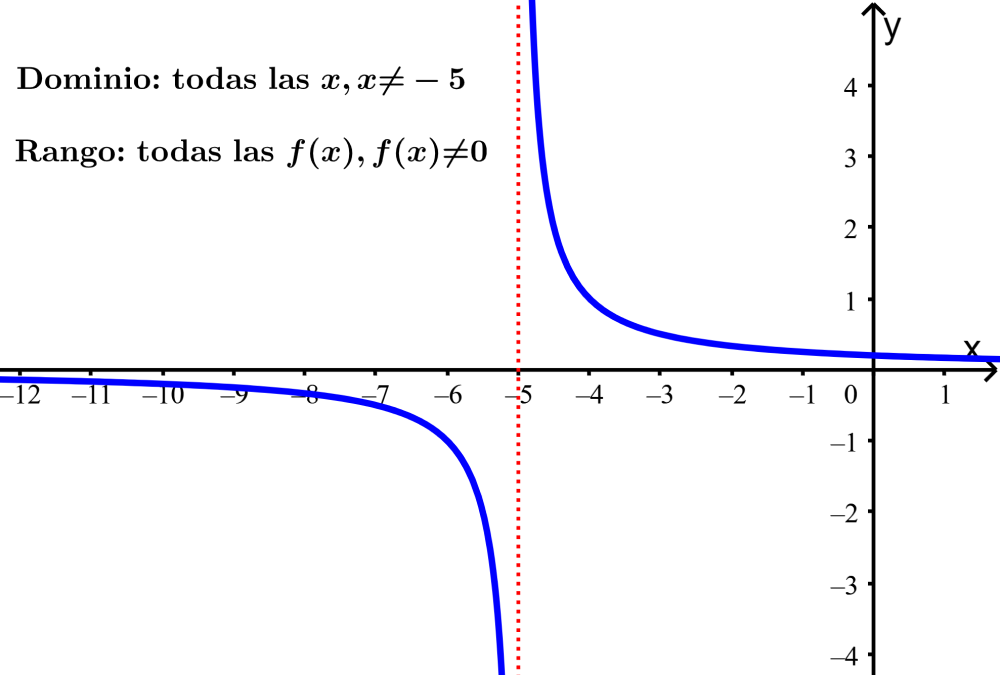
Encuentra el dominio y el rango para la función $latex f(x)=\frac{1}{x+5}$.
Dominio: La función $latex f(x)=\frac{1}{x+5}$ no está definida para $latex x=-5$ ya que este valor produciría una división por 0. Entonces, el dominio de la función es todos los números reales a excepción del -5.
Rango: Sin importar qué tan grande o qué tan pequeña sea la x, la función $latex f(x)$ nunca será igual a 0. Esto significa que el rango de la función es todos los números reales a excepción del 0.
En la gráfica podemos ver que la función no está definida para $latex x=-5$ y que el rango es todos los números enteros a excepción del 0:
EJEMPLO 3
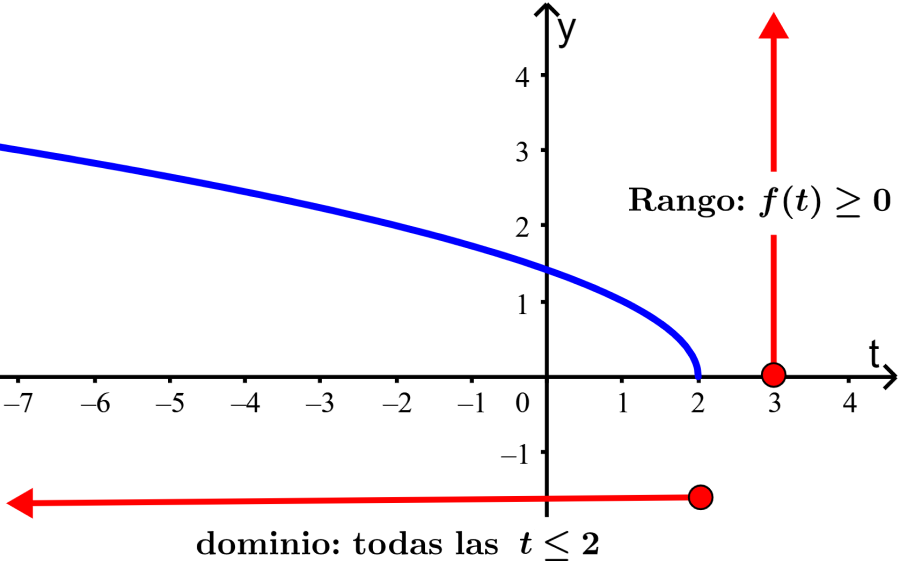
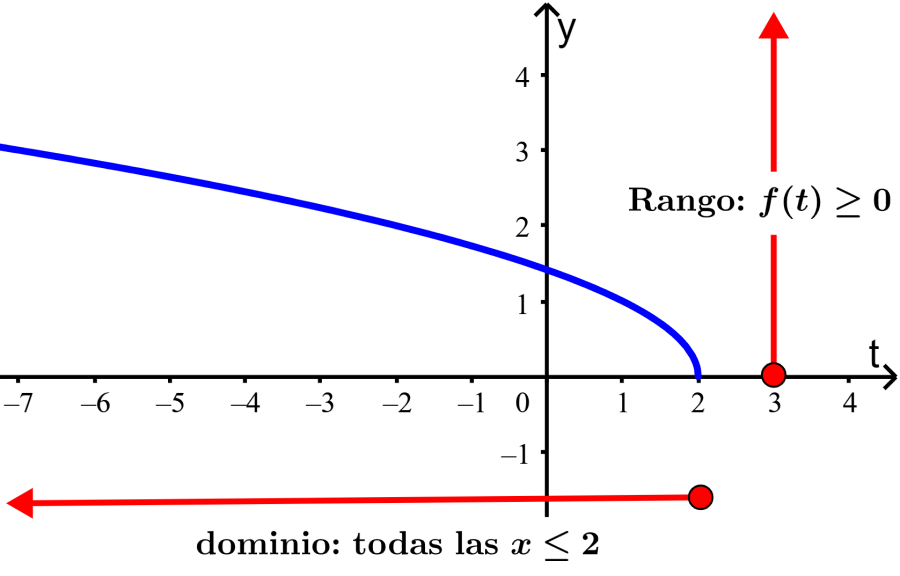
Encuentra el dominio y el rango para la función $latex f(t)=\sqrt{{2-t}}$.
Dominio: La función $latex f(t)=\sqrt{{2-t}}$ no está definida para valores mayores que 2, ya que haría que tengamos un valor negativo dentro del signo de raíz cuadrada. Entonces el dominio de la función es todos los números reales menores o iguales a 2, $latex t\le 2$.
Rango: Por definición tenemos $latex f(t)=\sqrt{{2-t}}\ge 0$.
En la gráfica podemos ver t no toma valores mayores que 2 y el rango es mayor o igual que 0:
Véase también
¿Interesado en aprender más sobre funciones? Mira estas páginas: