Las funciones de parte entera son dos funciones importantes que son usadas frecuentemente en matemáticas y en computación. Hay dos funciones de parte entera, la una es la función piso (o función suelo) y la otra es la función techo.
A continuación, miraremos las definiciones, propiedades y gráficas de estas funciones junto con varios ejemplos resueltos.
Función piso y techo definición
Función techo definición
Una función techo es una función en la cual el número entero sucesivo más pequeño es retornado. En otras palabras, la función piso de un número real x es el número entero más pequeño que es mayor o igual que el número x.
La notación usada para representar a la función techo es $latex \lceil ~ \rceil$. Entonces, la función techo es $latex f(x)=\lceil x \rceil$.
Función piso definición
la función piso, también conocida como la función suelo, es definida como una función que retorna el número entero más grande que es menor o igual que x. La notación usada para representar a la función piso es $latex \lfloor ~ \rfloor$. Entonces, la función piso es $latex f(x)=\lfloor x \rfloor$.
EJEMPLOS
- $latex \lceil 2.5 \rceil=3$
- $latex \lfloor 2.5 \rfloor=2$
- $latex \lceil 4.85 \rceil=5$
- $latex \lfloor 4.85 \rfloor=4$
Función piso y techo propiedades
Las funciones piso y techo tienen muchas propiedades útiles e interesantes. Las siguientes son algunas de las más importantes. Aquí, n es un número entero:
- $latex \lfloor x \rfloor=n$ sólo si es que $latex n\leq x<n+1$
- $latex \lceil x \rceil=n$ sólo si es que $latex n-1<x\leq n$
- $latex \lfloor x \rfloor=n$ sólo si es que $latex x-1< n\leq x$
- $latex \lceil x \rceil=n$ sólo si es que $latex x\leq n<x+1$
- $latex \lceil -x \rceil=-\lceil x \rceil$
- $latex \lfloor -x \rfloor=-\lfloor x \rfloor$
- $latex \lceil x+n \rceil=\lceil x \rceil +n$
- $latex \lfloor x+n \rfloor=\lfloor x \rfloor +n$
Función piso y techo fórmula
Fórmula de función techo
La fórmula para encontrar el valor techo para cualquier valor especificado es:
$latex f(x)=$ mínimo {$latex a\in Z; a\geq x$}
Esto significa que la función retorna el mínimo número entero que es mayor o igual que x. Esto es representado por:
$latex f(x)=<\lceil x \rceil=$ menor número entero sucesivo de x
Fórmula de función piso
La fórmula para encontrar el valor piso para cualquier valor especificado es:
$latex f(x)=$ mínimo {$latex a\in Z; a\geq x$}
Esto significa que la función retorna el máximo número entero que es menor o igual que x. Esto es representado por:
$latex f(x)=\lfloor x \rfloor=$ mayor número entero sucesivo de x
Gráficas de función piso y techo
Las gráficas de la función piso y techo tienen una forma de gradas y tienen una discontinuidad en cada punto de números enteros.
La siguiente es la gráfica de la función piso:
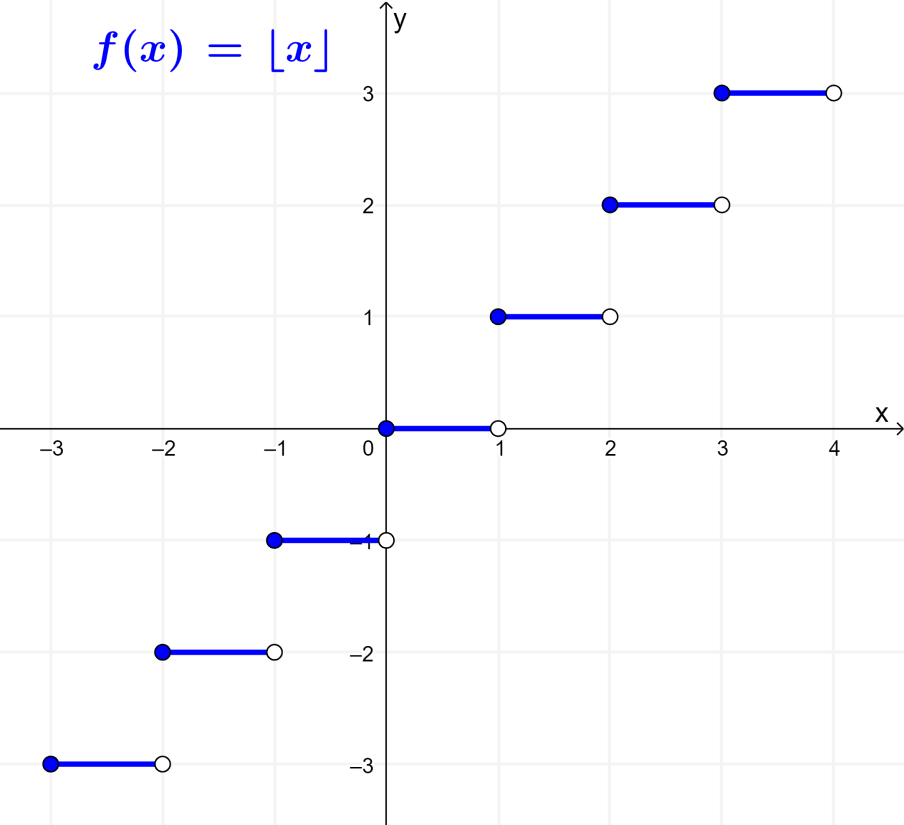
La siguiente es la gráfica de la función techo:
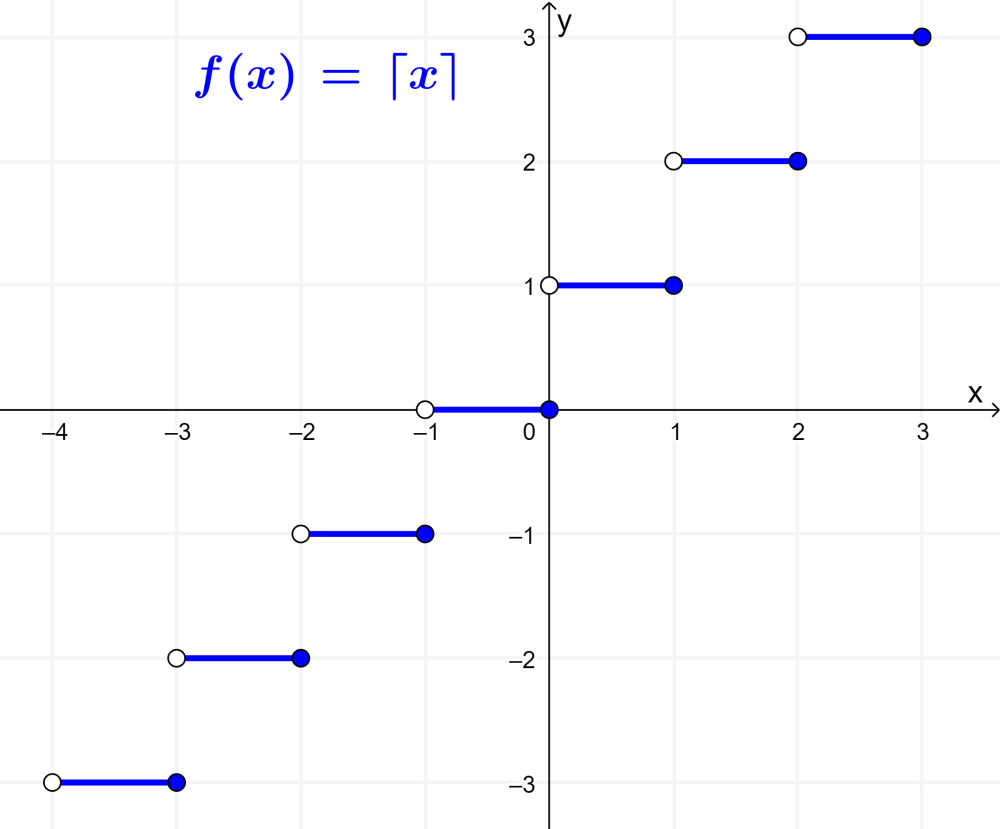
Función piso y techo ejemplos resueltos
EJEMPLO 1
Evalúa la función techo de 3.4 y de -3.4.
Solución: Tenemos $latex f(3.4)=\lceil 3.4 \rceil=4$ y $latex f(-3.4)=\lceil -3.4 \rceil=-3$.
La función techo de un número real es el menor número entero que es mayor o igual a x. En el caso de 3.4, los números enteros mayores son 4, 5, 6… El más pequeño de estos es el 4.
En el caso de -3.4, los números enteros mayores son -3, -2, -1, … El más pequeño de estos es -3.
EJEMPLO 2
¿Cuál es el resultado de $latex \lfloor \sqrt{46} \rfloor$?.
Solución: En este caso, tenemos que encontrar el mayor número entero que es igual o menor que $latex \sqrt{46}$.
Sabemos que $latex \sqrt{36}<\sqrt{46}<\sqrt{49}$.
Entonces, tenemos $latex 6<\sqrt{46}<7$.
Por lo tanto, $latex \lfloor \sqrt{46} \rfloor=6$.
EJEMPLO 3
Resuelve la ecuación $latex \lfloor x-\frac{1}{2} \rfloor +\lfloor x-\frac{5}{2} \rfloor +\lfloor x-\frac{9}{2} \rfloor =3$.
Solución: Podemos resolver este problema más fácilmente al usar la sustitución $latex x-\frac{1}{2}=z$. Entonces, tenemos la ecuación:
$latex \lfloor z \rfloor +\lfloor z-2 \rfloor +\lfloor z-4 \rfloor =3$
Usando la identidad $latex \lfloor x+n \rfloor =\lfloor x \rfloor +n$, obtenemos lo siguiente:
$latex \lfloor z \rfloor +\lfloor z \rfloor -2+\lfloor z \rfloor -4=3$
⇒ $latex 3\lfloor z \rfloor =9$
⇒ $latex \lfloor z \rfloor =3$
La última ecuación significa que $latex 3\leq z<4$. Al retornar a la variable x, tenemos:
$latex 3\leq x-\frac{1}{2}<4$
⇒ $latex 3\frac{1}{2}\leq x<4\frac{1}{2}$
⇒ $latex x\in[3.5, 4.5)$
Inténtalo tú mismo – Resuelve los ejercicios
Véase también
¿Interesado en aprender más sobre funciones? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
