Para determinar cuándo es una función y cuándo no, debemos observar las entradas y las salidas de la relación. Si es que las entradas de la relación producen una sola salida, entonces la relación sí es una función. Caso contrario, si las entradas producen dos o más salidas, la relación no es una función.
Definiciones
Relaciones
Una relación es un conjunto de entradas y de salidas, muchas veces escritas como pares ordenados (entradas, salidas). El conjunto de los primeros componentes de cada par ordenado es llamado el dominio y el conjunto de los segundos componentes de cada par ordenado es llamado el rango.
Por ejemplo, en los siguientes conjuntos de pares ordenados, los primeros números en cada par son los primeros cuatro números naturales y los segundos números son el triple de los primeros:
{(1, 3), (2, 6), (3, 9), (4, 12)}
El dominio es {1, 2, 3, 4} y el rango es {3, 6, 9, 12}.
Cada valor en el dominio también es conocido como entrada o como variable independiente y muchas veces es representado con la letra x. Cada valor en el rango también es conocido como salida o como variable dependiente y muchas veces es representado con la letra y.
Funciones
Una función es una relación que asigna un solo valor en el rango a cada valor en el dominio. Esto significa que los valores de x no se repiten. En el ejemplo que tenemos arriba, relacionamos a los cuatro primeros números naturales con el triple de estos números.
Esta relación sí es una función, ya que cada elemento en el dominio, {1, 2, 3, 4}, está emparejado con exactamente un elemento en el rango {3, 6, 9, 12}.
Ahora miremos otro ejemplo. Considera los siguientes pares ordenados, en donde relacionamos letras con números:
{(A, 1), (B, 2), (A, 3), (B, 4)}
Observa que cada elemento en el dominio {A, B}, no está emparejado con exactamente un elemento en el rango {1, 2, 3, 4}. Por ejemplo, la letra A corresponde a dos valores del rango {1, 3} y la letra B corresponde a dos valores del rango {2, 4}. Esto significa que esta relación no es una función.
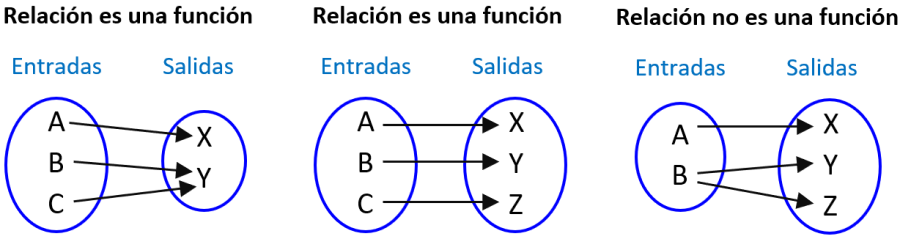
En la siguiente imagen podemos comparar relaciones que son funciones y no funciones:
¿Cómo determinar cuándo es una función y cuándo no?
Para determinar si es que es una función o no, podemos usar lo siguiente:
1. Identifica los valores de entradas.
2. Identifica los valores de salidas.
3. Si es que cada valor de entrada produce un solo valor de salida, la relación es una función. Si es que cada valor de entrada produce dos o más valores de salidas, la relación no es una función.
También podemos resolver gráficamente al usar la prueba de la línea en diagramas de mapeo o la prueba de la línea vertical para gráficas.
Prueba de la línea en diagramas de mapeo
Para verificar si es que una relación es una función usando diagramas de mapeo, usamos el siguiente criterio: si es que cada entrada tiene una sola línea conectada, entonces las salidas sí representan una función.
Por ejemplo, en el siguiente diagrama de mapeo, y es una función de x, pero x no es una función de y.
Prueba de la línea vertical para gráficas
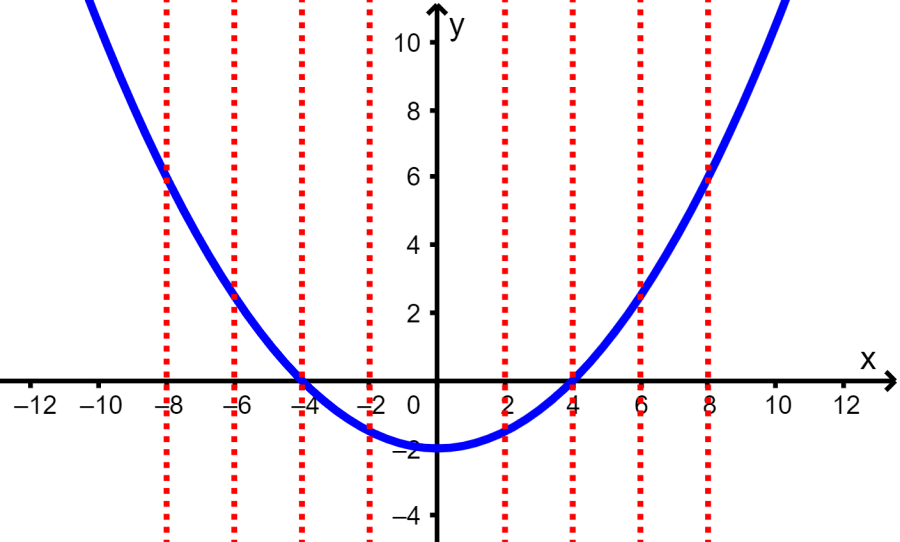
Para determinar si es que y es una función de x dada una gráfica de la relación, podemos usar el siguiente criterio: si es que todas las líneas verticales que pueden ser trazadas pasan por un solo punto en la gráfica, entonces la relación sí es una función. Si es que es posible trazar una línea vertical que pasa por al menos dos puntos en la gráfica, entonces la relación no es una función.
Por ejemplo, en la siguiente gráfica, podemos ver que y sí es una función de x:
Ejemplos resueltos
EJEMPLO 1
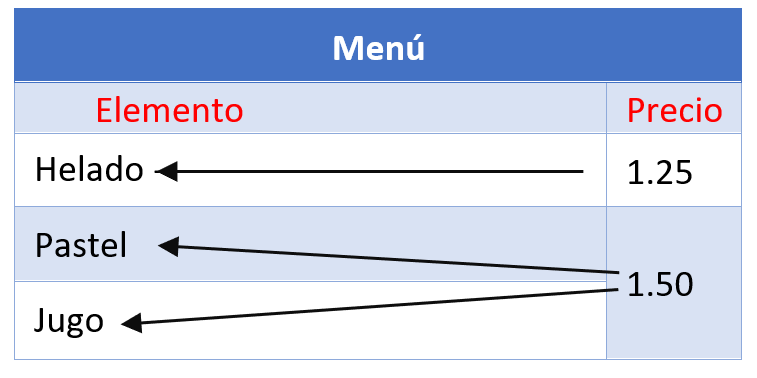
Determina si es que la lista de precios de un menú son funciones.
Tenemos el menú que se muestra en la imagen, el cual consiste de elementos y sus precios.
1. ¿Es el precio una función del elemento?
2. ¿Es el elemento una función del precio?
Solución:
1. Vamos a considerar a los elementos como las entradas. Entonces, los precios son los valores de salida. Cada elemento en el menú tiene un solo precio, por lo que el precio es una función del elemento.
2. Ahora consideremos a los precios como las entradas. Vemos que dos elementos del menú tienen el mismo precio. Esto significa que las entradas tienen más de un valor de salida asignado, por lo tanto no representa a una función. Los elementos no son una función del precio.
EJEMPLO 2
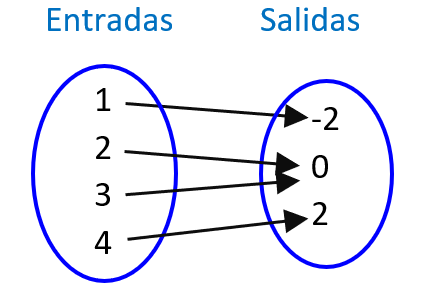
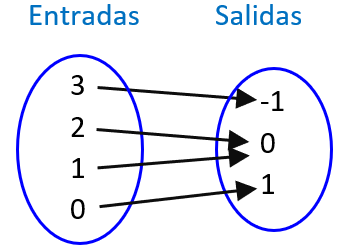
Determina si es que el siguiente diagrama de mapeo representa a una función.
Solución:
Fácilmente podemos observar que cada valor de entrada corresponde a un solo valor de salida, entonces, el diagrama de mapeo sí representa a una función.
EJEMPLO 3
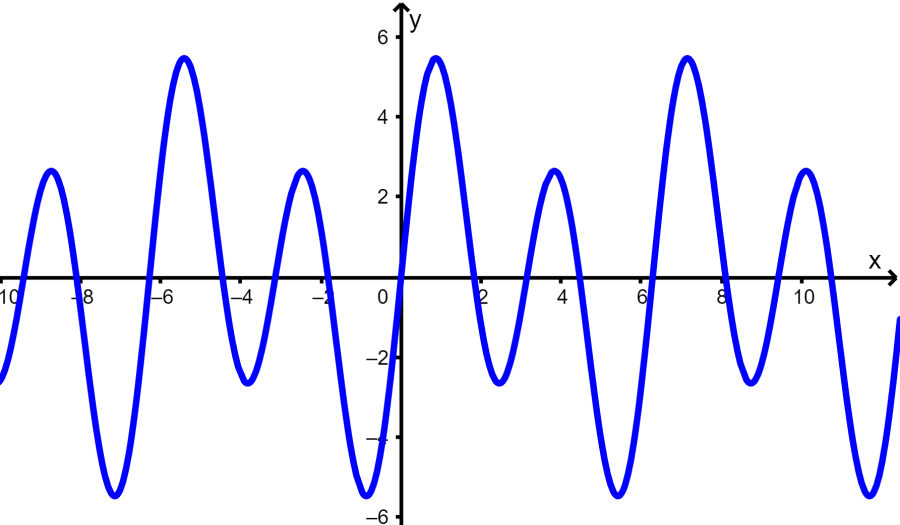
Determina si es que la siguiente gráfica representa a una función.
Solución: Podemos usar la prueba de la línea vertical para determinar si es que es una función o no:
Vemos que las líneas verticales trazadas cruzan a la función en un solo punto, por lo que la gráfica sí representa a una función.
EJEMPLO 4
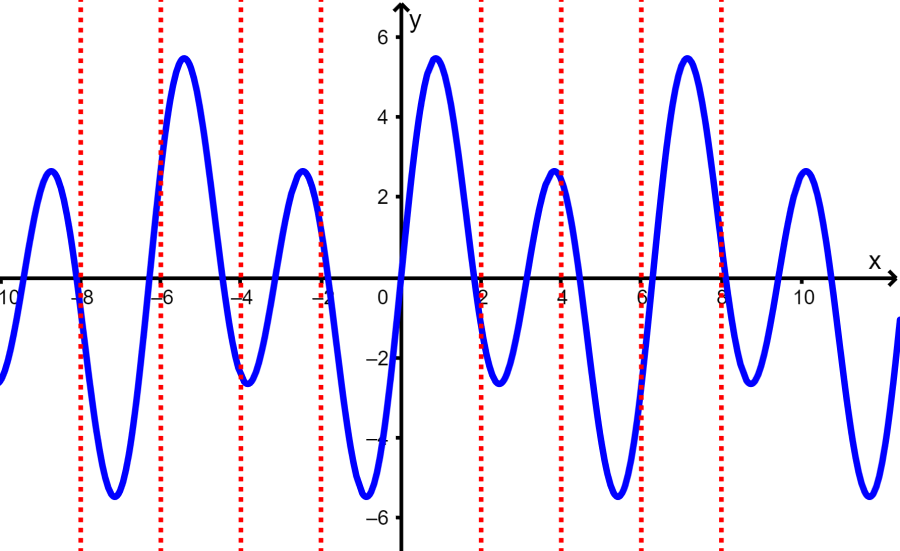
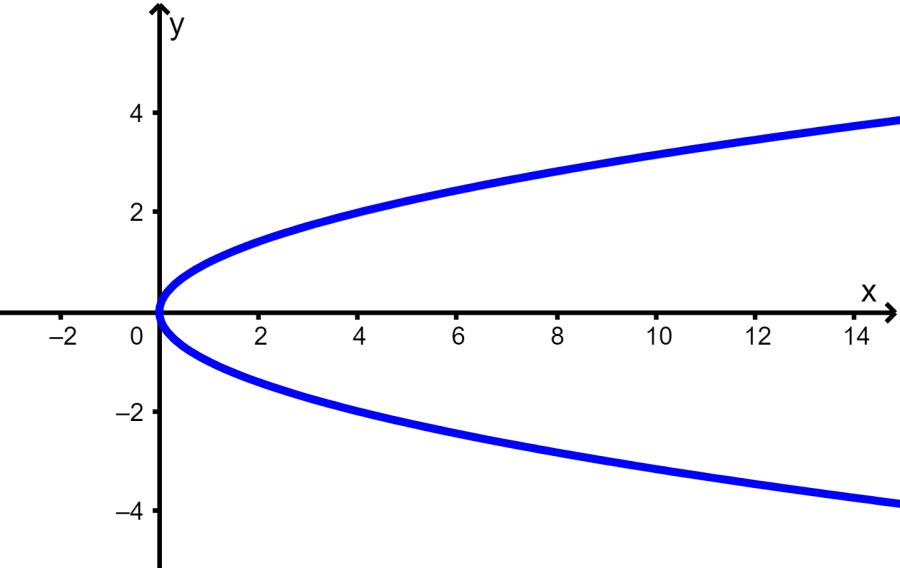
Determina si es que la siguiente gráfica representa a una función.
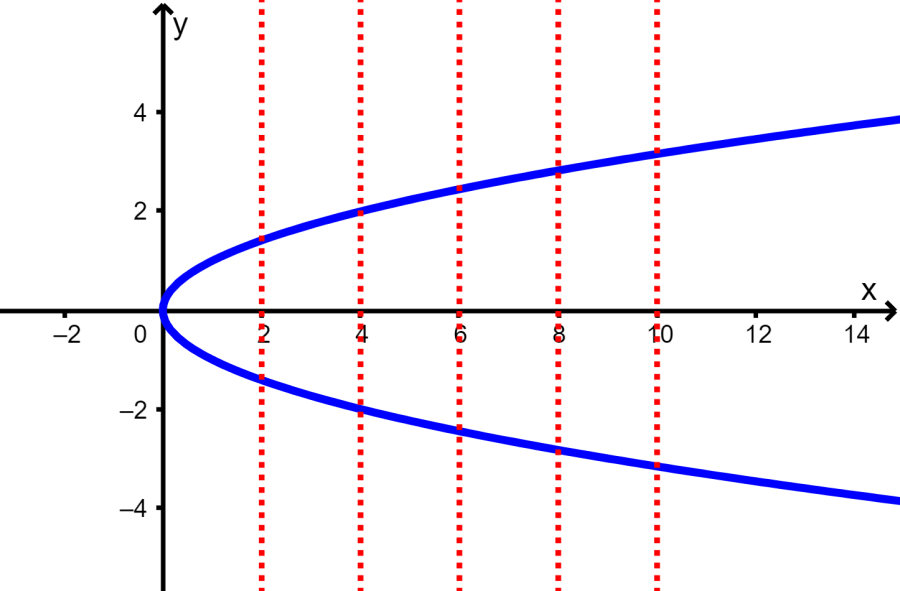
Solución: Nuevamente, usamos la prueba de la línea vertical para determinar si la gráfica es una función o no:
Al trazar varias líneas verticales, vemos que sí es posible que una línea vertical cruce a la gráfica en más de un solo punto. Esto significa que la gráfica no representa a una función.
Véase también
¿Interesado en aprender más sobre funciones? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
