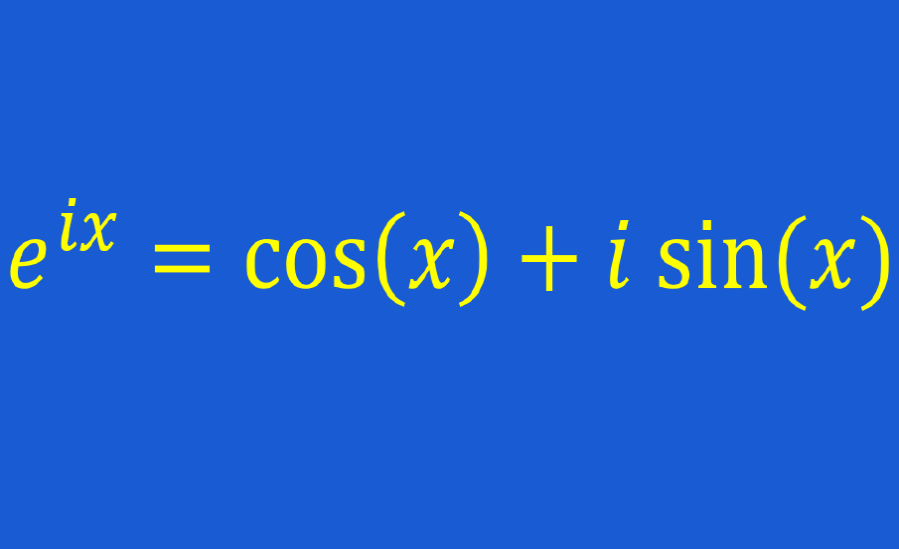En el estudio de los números complejos, así como también en la integración de expresiones trigonométricas, es muy probable que nos encontremos con la Fórmula de Euler. Esta fórmula, que es nombrada en honor al matemático Leonhard Euler, necesita una examinación cuidadosa para entender todo su potencial.
A continuación, miraremos las características de la fórmula de Euler e identificaremos cada una de sus partes constituyentes. Además, aprenderemos sobre sus varias aplicaciones como el caso particular de la identidad de Euler, la forma exponencial de números complejos, definiciones alternas de funciones y las identidades trigonométricas.
Interpretación de la fórmula de Euler
La fórmula de Euler nos indica lo siguiente:
| $latex {{e}^{ix}}=\cos(x)+i~\sin(x)$ |
En esta fórmula tenemos que:
- $latex x$ es un número real
- $latex e$ es la base del logaritmo natural (aproximadamente 2.718…)
- $latex i$ es la unidad imaginaria (raíz cuadrada de $latex -1$)
La fórmula de Euler establece la relación entre funciones trigonométricas y funciones exponenciales. Esta fórmula puede ser pensada geométricamente como una manera de relacionar a dos representaciones del mismo número complejo en el plano complejo.
Los siguientes son algunos valores clave de la fórmula de Euler que corresponden a puntos importantes en el círculo unitario:
- Para $latex x=0$, tenemos $latex {{e}^{0}}=\cos(0)+i~\sin(0)$, lo cual resulta en $latex 1=1$. Sabemos que un ángulo de 0 en el círculo unitario es igual a 1 en el eje real.
- Para $latex x=1$, tenemos $latex {{e}^{i}}=\cos(1)+i~\sin(1)$. Esto sugiere que $latex {{e}^i}$ es el punto en el círculo unitario con un ángulo de 1 radian.
- Para $latex x=\frac{\pi}{2}$, tenemos $latex {{e}^{i\frac{\pi}{2}}}=\cos(\frac{\pi}{2})+i~\sin(\frac{\pi}{2})$. Este resultado es aplicado frecuentemente en física.
- Para $latex x=\pi$, tenemos $latex {{e}^{i\pi}}=\cos(\pi)+i~\sin(\pi)$, lo cual resulta en $latex {{e}^{i\pi}}=-1$. El resultado es la identidad de Euler.
- Para $latex x=2\pi$, tenemos $latex {{e}^{i(2\pi)}}=\cos(2\pi)+i~\sin(2\pi)$, lo cual resulta en $latex {{e}^{i(2\pi)}}=1$. Similar al resultado de usar 0.
Identidad de Euler
La identidad de Euler es muchas veces considerada como la ecuación más hermosa en matemáticas. La identidad de Euler es escrita de la siguiente manera:
| $latex {{e}^{i\pi}}+1=0$ |
Esta ecuación contiene a las cinco constantes más importantes de matemáticas:
- La identidad aditiva 0
- La unidad 1
- La constante $latex \pi$ (cociente de una circunferencia a su radio)
- La base del logaritmo natural $latex e$
- La unidad imaginaria $latex i$
Aquí, tenemos a tres diferentes tipos de números: enteros, números irracionales y números imaginarios. También tenemos a tres de las operaciones matemáticas básicas: adición, multiplicación y exponenciación.
La identidad de Euler es obtenida al empezar con la fórmula de Euler:
$latex {{e}^{ix}}=\cos(x)+i~\sin(x)$
y al usar $latex x=\pi$ y mover el $latex -1$ resultante al lado izquierdo.
Usos de la fórmula de Euler
La fórmula de Euler puede ser usada para facilitar el cálculo de operaciones con números complejos, identidades trigonométricas e incluso integración de funciones. Con la fórmula de Euler podemos escribir a los números complejos en su forma exponencial, escribir definiciones alternas de funciones importantes y obtener identidades trigonométricas.
Números complejos en forma exponencial
Sabemos que un número complejo puede ser escrito en coordenadas cartesianas como $latex a+bi$, en donde a es la parte real y b es la parte imaginaria.
También sabemos que el mismo número complejo puede ser expresado en coordenadas polares como $latex r(\cos(\theta+i~\sin(\theta))$, en donde r es la magnitud del número y $latex \theta$ es su ángulo con respecto al eje x positivo.
Gracias a la fórmula de Euler, todos los números complejos pueden ser escritos como exponenciales de la siguiente manera:
$latex z=r(\cos(\theta+i~\sin(\theta))=r{{e}^{i\theta}}$
La forma exponencial de números complejos hace que la multiplicación de números complejos sea mucho más fácil. Por ejemplo, dados dos números complejos $latex z_{1}=r_{1}{{e}^{i\theta _{1}}}$ y $latex z_{2}=r_{2}{{e}^{i\theta _{2}}}$, podemos multiplicarlos de la siguiente manera:
$latex z_{1}z_{2}=r_{1}{{e}^{i\theta _{1}}}\times r_{2}{{e}^{i\theta _{2}}}$
$latex =r_{1}r_{2}{{e}^{i(\theta _{1}+\theta _{2})}}$
De igual forma, podemos dividir dos números complejos al dividir sus magnitudes y restar sus ángulos.
Definiciones alternas de funciones importantes
La fórmula de Euler también puede ser usada para obtener definiciones alternas para diferentes funciones importantes como las funciones trigonométricas y las funciones hiperbólicas.
Por ejemplo, también es posible usar la fórmula de Euler para derivar una ecuación similar para el ángulo opuesto $latex -x$:
$latex {{e}^{-ix}}=\cos(x)-i~\sin(x)$
Esta ecuación junto con la fórmula de Euler original, constituye un sistema de ecuaciones del cual podemos despejar tanto a la función seno como a la función coseno.
Por ejemplo, al restar la ecuación $latex {{e}^{-ix}}$ de la ecuación $latex {{e}^{ix}}$, los cosenos se cancelan y después de dividir por $latex 2i$, obtenemos una expresión para la función seno:
$latex \sin(x)=\frac{{{e}^{ix}}-{{e}^{-ix}}}{2i}$
De igual forma, al sumar las dos ecuaciones, los senos se cancelan y después de dividir por 2, obtenemos una expresión para la función coseno:
$latex \cos(x)=\frac{{{e}^{ix}}+{{e}^{-ix}}}{2}$
La función tangente puede ser obtenida al dividir al seno por el coseno. Usando métodos similares, expresiones para las funciones hiperbólicas y otras funciones importantes también pueden ser obtenidas.
Véase también
¿Interesado en aprender más sobre números complejos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
