Hasta ahora estamos familiarizados con escribir a números complejos en la forma $latex z=a+bi$. Sin embargo, existen formas alternativas de escribir a los números complejos que pueden resultar convenientes a la hora de resolver operaciones matemáticas con estos números.
A continuación, aprenderemos a escribir números complejos en forma polar. Veremos las fórmulas usadas para transformar a números complejos en su forma polar y miraremos varios ejercicios resueltos para aprender la aplicación de estas fórmulas.
Interpretación geométrica
Para entender de mejor manera las versiones alternas de los números complejos, debemos familiarizarnos con la interpretación geométrica de estos números, ya que nos guiará directamente a su forma polar.
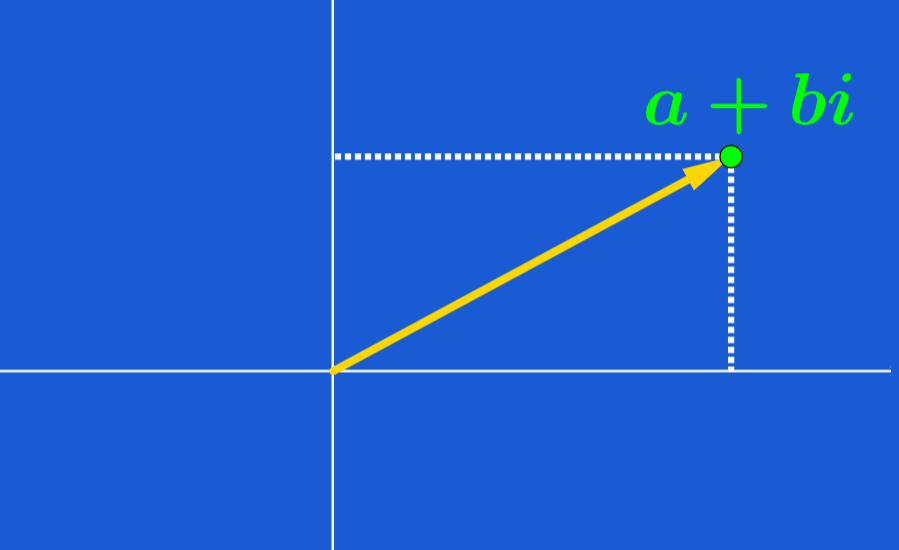
Consideremos al número complejo $latex z=a+bi$. Podemos pensar en este número como el punto $latex (a, b)$ en el sistema de coordenadas cartesianas o como el vector que empieza en el origen y termina en el punto $latex (a, b)$. La siguiente gráfica representa esto:
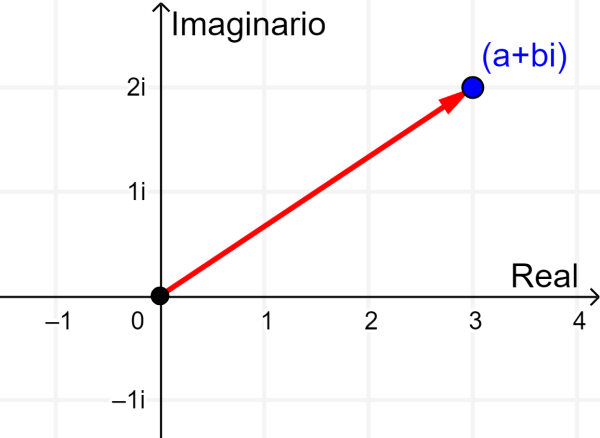
En esta interpretación, el eje x representa a los números reales y el eje y representa a los números imaginarios. Este plano muchas veces es denominado como el plano complejo.
Usando este plano, podemos obtener una interpretación geométrica del módulo o magnitud. Podemos ver que, $latex |z|=\sqrt{{{a}^2}+{{b}^2}}$ es simplemente la longitud del vector usado para representar al número $latex z=a+bi$.
Forma polar
La forma polar es una forma alternativa de escribir a números complejos. Si es que pensamos en el número complejo $latex z=a+bi$ como el punto $latex (a, b)$ en el plano complejo, sabemos que podemos representar a este punto usando las coordenadas polares $latex (r, \theta)$, en donde, r es la distancia del punto desde el origen y θ es el ángulo, generalmente en radianes, desde el eje x positivo hasta el vector que conecta al punto con el origen.
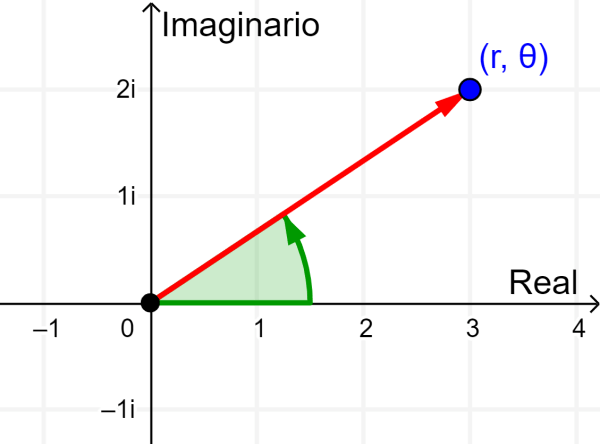
Cuando trabajamos con números complejos, asumimos que r es positivo y que θ puede ser cualquier ángulo posible tanto positivo como negativo que termina en el vector. Solo consideramos la forma polar de números complejos diferentes de cero, ya que el ángulo θ no está definido para el punto (0, 0).
Podemos convertir las coordenadas polares $latex (r, \theta)$ a las coordenadas cartesianas correspondientes del punto $latex (a, b)$ usando las siguientes fórmulas:
$latex a=r~\cos(\theta)$ $latex b=r ~\sin(\theta)$
De igual forma, también tenemos la siguiente fórmula para obtener r usando las coordenadas cartesianas a y b:
$latex r=\sqrt{{{a}^2}+{{b}^2}}$
El lado derecho de esta fórmula es la definición del módulo o magnitud del número complejo, entonces, tenemos:
$latex r=|z|$
Usando esto, podemos escribir a números complejos en su forma polar:
| $latex z=r(\cos(\theta)+i~\sin(\theta)$ $latex z=|z|(\cos(\theta)+i~\sin(\theta)$ |
El ángulo $latex \theta $ es llamado el argumento de z y es denotado por:
$latex \theta=arg(z)$
El argumento de z puede ser cualquiera de los infinitos valores posibles de $latex \theta$, los cuales pueden ser encontrados al resolver:
$latex \tan(\theta)=\frac{b}{a}$
y tenemos que asegurarnos que $latex \theta$ está en el cuadrante correcto.
Supongamos que tenemos un número complejo z con un argumento $latex \theta$. Si es que incrementamos el valor de $latex \theta$, estamos rotando al punto con respecto al origen en dirección contraria a las manecillas del reloj.
Dado que $latex 2\pi$ representa a una revolución completa, estaríamos nuevamente en el punto inicial cuando lleguemos a $latex \theta +2\pi$. Esto significa que $latex \theta $ y $latex \theta+2\pi$ son equivalentes.
Continuando con esta idea, cada vez que añadamos múltiplos de $latex 2\pi$, obtenemos un ángulo equivalente al ángulo original.
Operaciones de números complejos en forma polar
La forma polar de números complejos puede resultar en que algunas operaciones sean más fáciles.
Números iguales en forma polar
Para que dos números complejos sean iguales, sus módulos deben de ser los mismos y sus argumentos deben diferir por 2kπ, en donde, k es cualquier número entero.
Por ejemplo, si es que tenemos $$r(\cos (t)+i\sin (t))=R(\cos (T)+i\sin (T))$$, entonces, debemos tener $latex r=R$ y $latex T=t+2k\pi$.
Conjugado de un número complejo en forma polar
El número conjugado del número $latex a+bi$ es $latex a-bi$. En forma polar, el conjugado del número polar $latex r(\cos (t)+i\sin (t))$ es $latex r(\cos (-t)+i\sin (-t))$.
Producto de números complejos en forma polar
Para multiplicar dos números complejos en forma polar, tenemos que multiplicar sus módulos y sumar sus argumentos. Entonces, tenemos:
$$ r(\cos (t)+i\sin (t))\times R(\cos (T)+i\sin (T))$$
$latex =rR(\cos (t+T)+i\sin (t+T))$
División de números complejos en forma polar
Para dividir dos números complejos en forma polar, tenemos que dividir sus módulos y restar sus argumentos. Entonces, tenemos:
$$\frac{r(\cos (t)+i\sin (t))}{R(\cos (T)+i\sin (T))}$$
$latex =\frac{r}{R}(\cos (t-T)+i\sin (t-T))$
Ejercicios de números complejos en forma polar
Los siguientes ejercicios son algunos ejemplos de operaciones con números complejos en forma polar.
EJERCICIO 1
Si es que tenemos al número $latex 6+10i$, ¿cuál es su equivalente en forma polar?
Solución
Para transformar a un número complejo escrito en forma convencional a su forma polar, vamos a usar la fórmula indicada arriba. Entonces, tenemos:
$latex r=\sqrt{{{a}^2}+{{b}^2}}$
$latex =\sqrt{{{6}^2}+{{10}^2}}$
$latex =\sqrt{36+100}$
$latex =\sqrt{136}$
$latex =11.66$
$latex \tan(\theta)=\frac{b}{a}$
$latex \tan(\theta)=\frac{10}{6}$
$latex \theta={{\tan}^{-1}}(\frac{10}{6})$
$latex \theta=1.03$ rad
Entonces, la forma polar del número $latex 6+10i$ es $latex 11.6(\cos(1.03)+i\sin(1.03))$.
EJERCICIO 2
¿Cuál es el conjugado del número $latex 5(\cos(1.8)+i\sin(1.8))$?
Solución
Para encontrar el conjugado de un número complejo escrito en forma polar, tenemos que escribir al módulo sin ningún cambio y cambiar al argumento con un signo negativo. Entonces, el conjugado del número complejo dado es:
$latex 11.6(\cos(-1.03)+i\sin(-1.03))$
EJERCICIO 3
¿Cuál es el producto de los números $latex 5(\cos(0.8)+i\sin(0.8))$ y $latex 8(\cos(1.6)+i\sin(1.6))$?
Solución
Para obtener el producto de dos números complejos escritos en forma polar, tenemos que multiplicar sus módulos y sumar sus argumentos. Entonces, tenemos:
$$5(\cos(0.8)+i\sin(0.8))\times 8(\cos(1.6)+i\sin(1.6))$$
$latex =40(\cos(2.4)+i\sin(2.4))$
EJERCICIO 4
¿Cuál es el resultado de la división? $$\frac{24(\cos(2.7)+i\sin(2.7))}{6(\cos(1.5)+i\sin(1.5))}$$
Solución
Para dividir dos números complejos escritos en forma polar, tenemos que dividir sus módulos y restar sus argumentos. Entonces, tenemos:
$$\frac{24(\cos(2.7)+i\sin(2.7))}{6(\cos(1.5)+i\sin(1.5))}$$
$$=\frac{24}{6}(\cos(2.7-1.5)+i\sin(2.7-1.5))$$
$latex =4(\cos(1.2)+i\sin(1.2))$
Véase también
¿Interesado en aprender más sobre números complejos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
