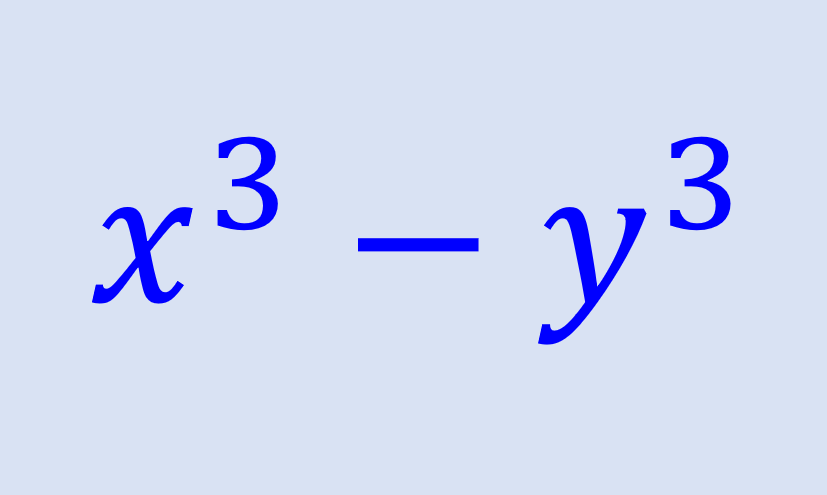Factorización de Diferencia de Cubos

Paso 1: En este caso, los términos no tienen ningún factor común, por lo que no podemos factorizar inicialmente.

Paso 2: Reescribimos al problema original como una diferencia de dos cubos perfectos:

⇒  $latex {{(x)}^3}-{{(2)}^3}$

Paso 3: a) Si es que eliminamos los paréntesis e ignoramos los cubos, vemos a la expresión:

$latex x-2$

b) Si es que elevamos al cuadrado al primer término, x, tenemos $latex {{x}^2}$. Si es multiplicamos los términos x y 2, tenemos $latex 2x$. Si es que elevamos al cuadrado al segundo término, 2, tenemos 4.

$latex {{x}^2},~~2x,~~4$

c) “Negativo, Positivo, Positivo”. Estos son los signos del problema.

Paso 4: La respuesta final es:

$latex (x-2)({{x}^2}+2x+4)$

Paso 1: No tenemos factores comunes en los términos, por lo que no podemos factorizar inicialmente.

Paso 2: Tenemos que reescribir al problema original como una diferencia de dos cubos perfectos:

⇒  $latex {{(2x)}^3}-{{(3)}^3}$

Paso 3: a) Ignorando los paréntesis y cubos, vemos a la expresión:

$latex 2x-3$

b) Elevando al cuadrado al primer término, x, tenemos $latex 4{{x}^2}$. Multiplicando a los términos 2x y 3, tenemos $latex 6x$. Elevando al cuadrado al segundo término, 3, tenemos 9.

$latex 4{{x}^2},~~6x,~~9$

c) “Negativo, Positivo, Positivo”. Estos son los signos del problema.

Paso 4: La respuesta final es:

$latex (2x-3)(4{{x}^2}+6x+9)$

Paso 1: Esta expresión tampoco puede ser factorizada inicialmente, ya que no hay factores comunes en los términos.

Paso 2: Reescribimos al problema original como una diferencia de dos cubos perfectos:

⇒  $latex {{(3x)}^3}-{{(5)}^3}$

Paso 3: a) Al ignorar a los paréntesis y los cubos, vemos a la expresión:

$latex 3x-5$

b) Al elevar al cuadrado al primer término, 3x, tenemos $latex 9{{x}^2}$. Al multiplicar a los términos 3x y 5, tenemos $latex 15x$. Al elevar al cuadrado al segundo término, 5, tenemos 25.

$latex 9{{x}^2},~~15x,~~25$

c) “Negativo, Positivo, Positivo”. Estos son los signos del problema.

Paso 4: La versión factorizada es:

$latex (3x-5)(9{{x}^2}+15x+25)$

Paso 1: Los términos no tienen ningún factor común, por lo que continuamos con los siguientes pasos.

Paso 2: Escribimos a la expresión original como una diferencia de dos cubos perfectos:

⇒  $latex {{(5x)}^3}-{{(6y)}^3}$

Paso 3: a) Si es que ignoramos a los paréntesis y los cubos, vemos a la expresión:

$latex 5x-6y$

b) Elevamos al cuadrado al primer término, 5x, para obtener $latex 25{{x}^2}$. Multiplicamos los términos 5x y 6y, para obtener $latex 30xy$. Elevamos al cuadrado al segundo término, 6y, para obtener $latex 36{{y}^2}$.

$latex 25{{x}^2},~~30xy,~~36{{y}^2}$

c) “Negativo, Positivo, Positivo”. Estos son los signos del problema.

Paso 4: La respuesta final es:

$latex (5x-6y)(25{{x}^2}+30xy+36{{y}^2})$

Paso 1: Esta expresión sí tiene factores comunes. Podemos extraer el 2 de ambos términos:

$latex 2(27{{x}^3}-8{{y}^3})$

Paso 2: Reescribimos a la expresión obtenida como una diferencia de dos cubos perfectos:

⇒  $latex 2({{(3x)}^3}-{{(2y)}^3})$

Paso 3: a) Al eliminar los paréntesis e ignorar los cubos, tenemos:

$latex 3x-2y$

b) Si es que elevamos al cuadrado al primer término, 3x, tenemos $latex 9{{x}^2}$. Si es multiplicamos los términos 3x y 2y, tenemos $latex 6xy$. Si es que elevamos al cuadrado al segundo término, 2y, tenemos $latex 4{{y}^2}$.

$latex 9{{x}^2},~~6xy,~~4{{y}^2}$

c) “Negativo, Positivo, Positivo”. Estos son los signos del problema.

Paso 4: Obtuvimos la siguiente factorización:

$latex 2(3x-2y)(9{{x}^2}+6xy+4{{y}^2})$

Paso 1: No tenemos factores comunes.

Paso 2: Al reescribir a la expresión como una diferencia de dos cubos perfectos, tenemos:

⇒  $latex {{(1)}^3}-{{(5xy)}^3}$

Paso 3: a) Si es que eliminamos los paréntesis e ignoramos los cubos, vemos a la expresión:

$latex 1-5xy$

b) Elevando al cuadrado al primer término, 1, tenemos 1. Multiplicando los términos 1 y 5xy, obtenemos $latex 5xy$. Elevando al cuadrado al segundo término, 5xy, tenemos $latex 25{{x}^2}{{y}^2}$.

$latex 1,~~5xy,~~25{{x}^2}{{y}^2}$

c) “Negativo, Positivo, Positivo”. Estos son los signos del problema.

Paso 4: La respuesta final es:

$latex (1-5xy)(1+5xy+25{{x}^2}{{y}^2})$