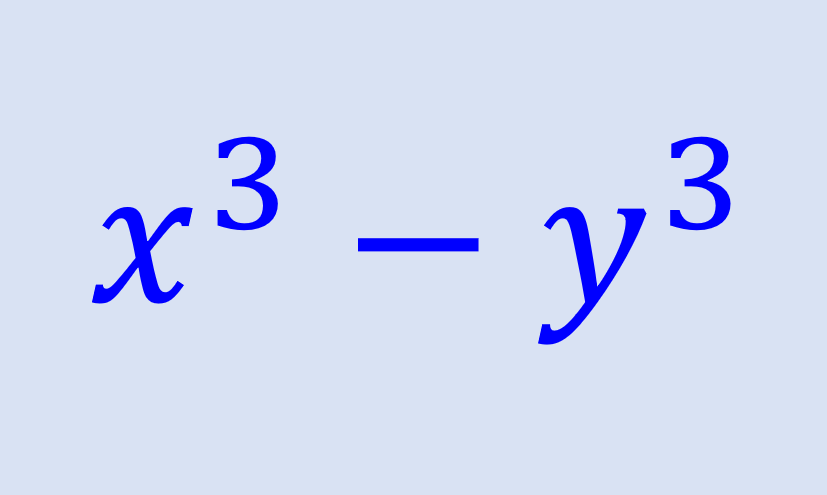Los binomios al cubo pueden tener la forma de una suma de cubos o una diferencia de cubos. Estos binomios pueden ser factorizados fácilmente usando fórmulas generales. El proceso usado para factorizar ambos binomios es similar con un simple cambio en los signos de la expresión final.
A continuación, haremos una revisión del proceso usado para obtener la factorización de binomios al cubo. Además, veremos varios ejercicios resueltos para entender la aplicación de ese proceso.
ÁLGEBRA
Relevante para…
Aprender sobre la factorización de binomios al cubo con ejercicios.
ÁLGEBRA
Relevante para…
Aprender sobre la factorización de binomios al cubo con ejercicios.
Factorizar la suma y diferencia de cubos
Podemos tener dos tipos de binomios al cubo, una diferencia o una suma. La suma de cubos es una expresión con la forma general $latex {{a}^3}+{{b}^3}$ y una diferencia de cubos es una expresión con la forma general $latex {{a}^3}-{{b}^3}$.
Para factorizar a binomios al cubo, podemos seguir los siguientes pasos:
Paso 1: Factorizar el factor común de los términos si es que existe para obtener una expresión más simple. No debemos olvidar incluir al factor común en la respuesta final.
Paso 2: Tenemos que reescribir a la expresión como una suma o diferencia de dos cubos perfectos.
Paso 3: Podemos escribir la respuesta usando las siguientes frases:
a) “Escribe lo que ves”
b) “Eleva al cuadrado – Multiplica – Eleva al cuadrado”
c) Si es que es una suma de cubos, tenemos los signos “Positivo, Negativo, Positivo” y si es que es una diferencia de cubos, tenemos los signos “Negativo, Positivo, Positivo”
Paso 4: Unimos las partes resultantes para obtener la expresión final factorizada.
Ejercicios de factorización de binomios al cubo resueltos
Los siguientes ejercicios de factorización de binomios al cubo aplican el proceso de resolución detallado arriba. Es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Factoriza al binomio $latex {{x}^3}+8$.
Solución
Paso 1: No tenemos ningún factor común para factorizar, por lo que no podemos simplificar.
Paso 2: Tenemos que reescribir al problema original como una suma de dos cubos perfectos:
⇒ $latex {{(x)}^3}+{{(2)}^3}$
Paso 3: a) Si es que ignoramos los paréntesis y los cubos, vemos a la expresión:
$latex x+2$
b) Al elevar al cuadrado al primer término, x, obtenemos $latex {{x}^2}$. Al multiplicar los términos x y 2, obtenemos $latex 2x$. Al elevar al cuadrado al segundo término, 2, tenemos 4.
$latex {{x}^2},~~2x,~~4$
c) Esta es una suma de binomios al cubo, por lo que los signos son “Positivo, Negativo, Positivo”.
Paso 4: La expresión factorizada es:
$latex (x+2)({{x}^2}-2x+4)$
EJERCICIO 2
Factoriza la expresión $latex {{x}^3}-27$.
Solución
Paso 1: Aquí, tampoco tenemos factores comunes, por lo que no podemos factorizar inicialmente.
Paso 2: Ahora, escribimos al problema original como una diferencia de dos cubos perfectos:
⇒ $latex {{(x)}^3}-{{(3)}^3}$
Paso 3: a) Si eliminamos los paréntesis y los cubos, vemos a la expresión:
$latex x-3$
b) Elevando al cuadrado al primer término, x, tenemos $latex {{x}^2}$. Multiplicando a los términos x y 3, tenemos $latex 3x$. Elevando al cuadrado al segundo término, 3, tenemos 9.
$latex {{x}^2},~~3x,~~9$
c) Esta es una diferencia de cubos, por lo que los signos que tenemos que usar son “Negativo, Positivo, Positivo”.
Paso 4: La expresión factorizada es:
$latex (x-3)({{x}^2}+3x+9)$
EJERCICIO 3
Obtén la factorización de la suma de cubos $latex 8{{x}^3}+125$.
Solución
Paso 1: No podemos factorizar esta expresión inicialmente, ya que no hay factores comunes.
Paso 2: Podemos reescribir a la expresión como una suma de dos cubos perfectos:
⇒ $latex {{(2x)}^3}-{{(5)}^3}$
Paso 3: a) Si ignoramos los paréntesis y los cubos, tenemos la expresión:
$latex 2x-5$
b) Si es que elevamos al cuadrado al primer término, 2x, tenemos $latex 4{{x}^2}$. Si es que multiplicamos a los términos 2x y 5, tenemos $latex 10x$. Si es que elevamos al cuadrado al segundo término, 5, tenemos 25.
$latex 4{{x}^2},~~10x,~~25$
c) Para una suma de cubos, debemos usar los signos “Positivo, Negativo, Positivo”.
Paso 4: La expresión factorizada es:
$latex (2x+5)(4{{x}^2}-10x+25)$
EJERCICIO 4
Factoriza la diferencia de cubos $latex 27{{x}^3}-216{{y}^3}$.
Solución
Paso 1: No podemos factorizar inicialmente porque no tenemos factores comunes.
Paso 2: Escribimos a la expresión como una diferencia de dos cubos perfectos:
⇒ $latex {{(3x)}^3}-{{(6y)}^3}$
Paso 3: a) Al eliminar paréntesis y cubos, tenemos la expresión:
$latex 3x-6y$
b) Elevando al cuadrado al primer término, 3x, tenemos $latex 9{{x}^2}$. Al multiplicar a los términos 3x y 6y, obtenemos $latex 18xy$. Si es que elevamos al cuadrado al segundo término, 6y, obtenemos $latex 36{{y}^2}$.
$latex 9{{x}^2},~~18xy,~~36{{y}^2}$
c) Para una diferencia de cubos, tenemos los signos “Negativo, Positivo, Positivo”.
Paso 4: La expresión factorizada final es:
$latex (3x-6y)(9{{x}^2}+18xy+36{{y}^2})$
EJERCICIO 5
Factoriza la suma de cubos $latex 54{{x}^3}+16{{y}^3}$.
Solución
Paso 1: Aquí sí tenemos un factor común, el 2. Podemos extraer el 2 de ambos términos:
$latex 2(27{{x}^3}+8{{y}^3})$
Paso 2: Ahora, podemos escribir a la expresión como una suma de dos cubos perfectos:
⇒ $latex 2({{(3x)}^3}+{{(2y)}^3})$
Paso 3: a) Si es que ignoramos los paréntesis y los cubos, tenemos:
$latex 3x+2y$
b) El primer término, 3x, al cuadrado es igual a $latex 9{{x}^2}$. El producto de los términos 3x y 2y es $latex 6xy$. El cuadrado del segundo término, 2y, es $latex 4{{y}^2}$.
$latex 9{{x}^2},~~6xy,~~4{{y}^2}$
c) Para una suma de cubos, tenemos los signos “Positivo, Negativo, Positivo”.
Paso 4: Obtuvimos la siguiente factorización:
$latex 2(3x+2y)(9{{x}^2}-6xy+4{{y}^2})$
EJERCICIO 6
Obtén la factorización de $latex 8-27{{x}^3}{{y}^3}$.
Solución
Paso 1: No tenemos ningún factor común en los términos.
Paso 2: Si es que reescribimos a la expresión como una diferencia de dos cubos perfectos, tenemos:
⇒ $latex {{(2)}^3}-{{(3xy)}^3}$
Paso 3: a) Si es que eliminamos los paréntesis e ignoramos los cubos, vemos a la expresión:
$latex 2-3xy$
b) El primer término, 1, al cuadrado es 8. El producto de los términos 2 y 3xy es $latex 6xy$. El segundo término, 3xy al cuadrado es $latex 9{{x}^2}{{y}^2}$.
$latex 8,~~6xy,~~9{{x}^2}{{y}^2}$
c) Para una diferencia de cubos, los signos son “Negativo, Positivo, Positivo”.
Paso 4: La expresión factorizada es:
$latex (2-3xy)(8+6xy+9{{x}^2}{{y}^2})$
Ejercicios de factorización de binomios al cubo para resolver
Practica lo aprendido sobre factorización de binomios al cubo con los siguientes ejercicios. Si necesitas ayuda, puedes mirar los ejercicios resueltos que se muestran arriba.
Véase también
¿Interesado en aprender más sobre factorización de expresiones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
