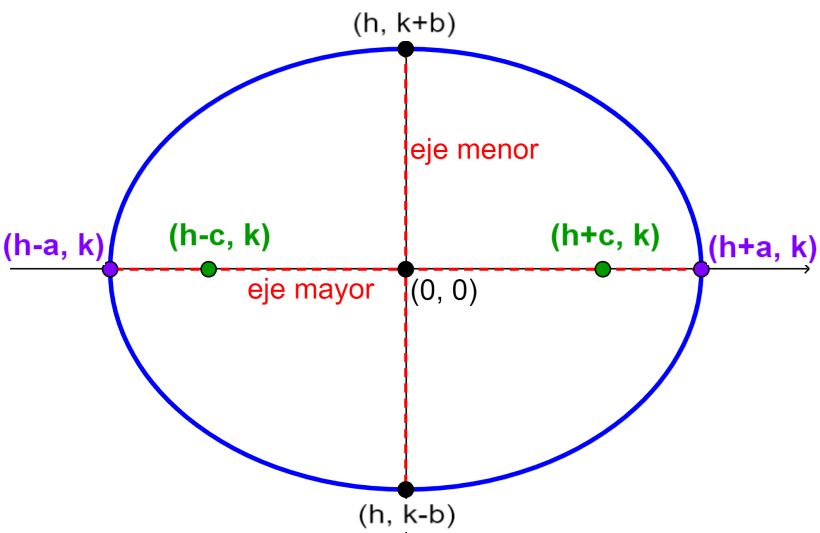
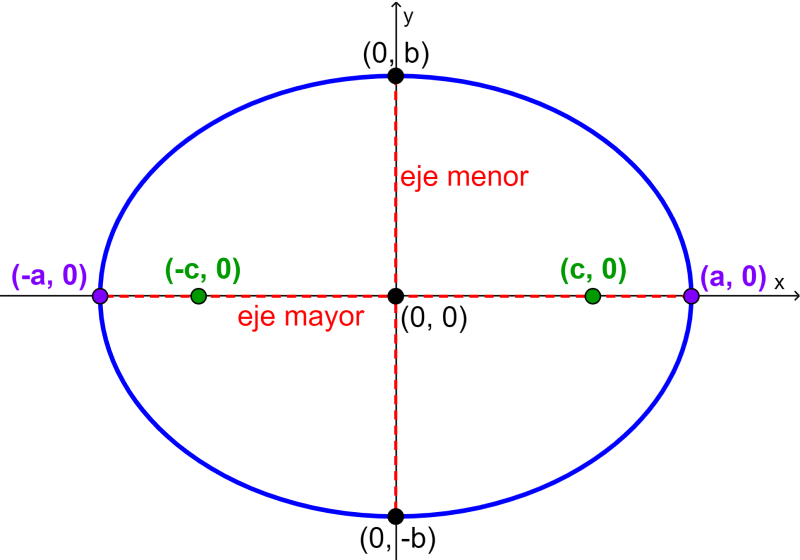
La excentricidad de la elipse es una característica única que determina la forma que tendrá la elipse. La excentricidad significa la desviación de la curva que ha ocurrido de la circularidad de una figura dada. Entonces, una excentricidad de 0 significa que la figura es completamente redonda y una excentricidad menor a 1 significa que la figura es un óvalo. La excentricidad depende de la distancia desde el centro hasta los focos y la distancia desde el centro hasta el vértice.
A continuación, conoceremos la fórmula usada para calcular la excentricidad de elipses. Resolveremos algunos ejercicios de práctica.
PRECÁLCULO
Relevante para…
Aprender sobre la excentricidad de la elipse con ejercicios.
PRECÁLCULO
Relevante para…
Aprender sobre la excentricidad de la elipse con ejercicios.
¿Cómo calcular la excentricidad de las elipses?
La excentricidad de las elipses es calculada usando la siguiente fórmula:
$latex e=\frac{c}{a}$
en donde, c representa a la distancia desde el centro hasta los focos y a representa a la longitud del semieje mayor, es decir, la distancia desde el centro hasta el vértice.
Podemos calcular la distancia desde el centro hasta los focos usando la fórmula:
$latex {{c}^2}={{a}^2}-{{b}^2}$
en donde, a es la longitud del semieje mayor y b es la longitud del semieje menor.
Sabemos que los focos de la elipse están más cerca del centro en comparación con los vértices. Esto significa que el valor de la excentricidad de una elipse siempre será menor que 1 ya que el valor del numerador siempre será menor que el valor del denominador.
Entre más se acercan los focos al centro, el valor de la excentricidad disminuye y cuando los focos están en el centro, la excentricidad es igual a 0 y la figura es redonda. Es decir, cuando tenemos $latex e=0$, ya no tenemos una elipse sino un círculo. Entonces, para una elipse, tenemos:
$latex e=\frac{c}{a}$, en donde $latex 0<e<1$
Ejercicios de excentricidad de elipses resueltos
Los siguientes ejercicios de excentricidad de elipses pueden ser usados para mirar la aplicación de las fórmulas vistas arriba. Intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
¿Cuál es la excentricidad de una elipse que tiene la ecuación $latex \frac{{{x}^2}}{64}+\frac{{{y}^2}}{16}=1$?
Solución
De la ecuación, podemos identificar a los siguientes valores:
$latex {{a}^2}=64$
$latex a=8$
$latex {{b}^2}=16$
$latex b=4$
Ahora, usamos estos valores para encontrar a c con la siguiente ecuación:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex {{c}^2}=64-16$
$latex {{c}^2}=48$
$latex c=6.93$
Reemplazamos a los valores encontrados en la ecuación de la excentricidad:
$latex e=\frac{c}{a}$
$latex e=\frac{6.93}{8}$
$latex e=0.87$
EJERCICIO 2
Si es que una elipse que tiene la ecuación $latex \frac{{{x}^2}}{81}+\frac{{{y}^2}}{25}=1$, ¿cuál es su excentricidad?
Solución
Empezamos identificando los valores de a y b de la ecuación dada:
$latex {{a}^2}=81$
$latex a=9$
$latex {{b}^2}=25$
$latex b=5$
Encontramos al valor de c usando la siguiente ecuación:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex {{c}^2}=81-25$
$latex {{c}^2}=56$
$latex c=7.48$
Usando la fórmula de la excentricidad con los valores encontrados, tenemos:
$latex e=\frac{c}{a}$
$latex e=\frac{7.48}{9}$
$latex e=0.83$
EJERCICIO 3
¿Cuál es la excentricidad de una elipse que tiene la ecuación $latex \frac{{{x}^2}}{121}+\frac{{{y}^2}}{64}=1$?
Solución
Podemos extraer los siguientes valores de la ecuación dada:
$latex {{a}^2}=121$
$latex a=11$
$latex {{b}^2}=64$
$latex b=8$
Al usar a estos valores, podemos encontrar a c con la siguiente ecuación:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex {{c}^2}=121-64$
$latex {{c}^2}=57$
$latex c=7.55$
Encontramos la excentricidad usando los valores encontrados:
$latex e=\frac{c}{a}$
$latex e=\frac{7.55}{11}$
$latex e=0.69$
EJERCICIO 4
Tenemos a una elipse con la ecuación $latex \frac{{{x}^2}}{144}+\frac{{{y}^2}}{121}=1$. ¿Cuál es su excentricidad?
Solución
Tenemos los siguientes valores:
$latex {{a}^2}=144$
$latex a=12$
$latex {{b}^2}=121$
$latex b=11$
Encontramos el valor de c usando a estos valores en la siguiente ecuación:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex {{c}^2}=144-121$
$latex {{c}^2}=23$
$latex c=4.8$
Usando estos datos en la ecuación de la excentricidad, tenemos:
$latex e=\frac{c}{a}$
$latex e=\frac{4.8}{11}$
$latex e=0.44$
Ejercicios de excentricidad de elipses para resolver
Usa lo aprendido sobre la excentricidad de las elipses para resolver los siguientes ejercicios. Selecciona una respuesta y verifícala para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre elipses? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
