Las elipses son secciones cónicas formadas cuando un plano interseca a un cono en una forma inclinada. La característica principal de las elipses es que todos los puntos en su curva tienen una suma de distancias desde dos puntos fijos que es igual a una constante. Los dos puntos fijos son denominados los focos de la elipse.
A continuación, veremos una definición más detallada de las elipses junto con una ilustración para visualizarla. Luego, conoceremos las características más importantes de estas secciones cónicas.
PRACÁLCULO
Relevante para…
Conocer las características fundamentales de las elipses.
PRACÁLCULO
Relevante para…
Conocer las características fundamentales de las elipses.
Definición de una elipse
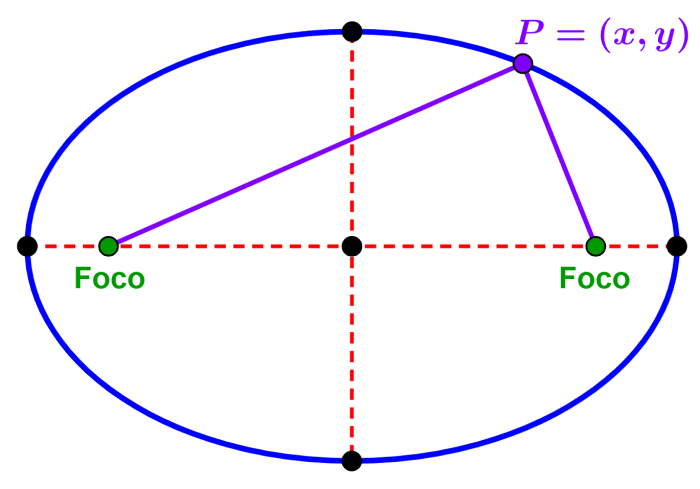
Las elipses son definidas como el conjunto de todos los puntos en el plano cartesiano, los cuales tienen dos distancias desde dos puntos fijos que suman para obtener siempre una constante. Esos dos puntos son conocidos como los focos de la elipse y sirven para definirla.
Adicionalmente, podemos definir a las elipses como secciones cónicas que son obtenidas por la intersección de un plano con un cono cuando el plano es inclinado a un ángulo con respecto a la base del cono.
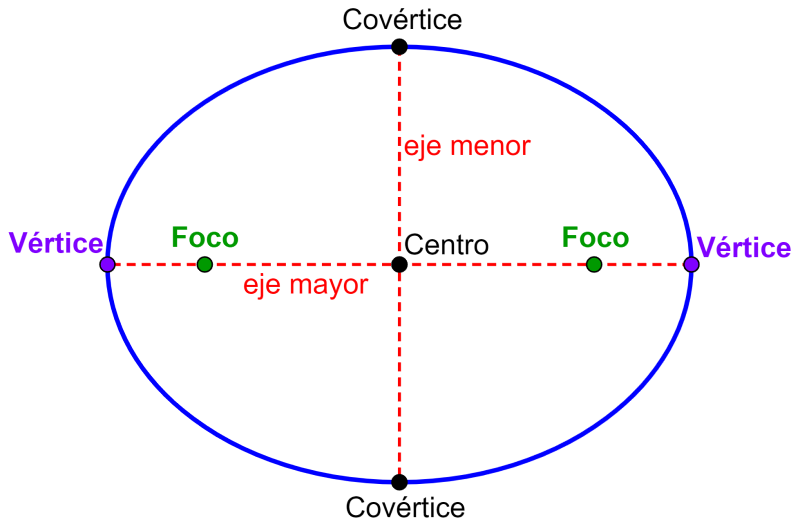
Las elipses tienen dos ejes de simetría, el eje mayor y el eje menor. El eje mayor es el diámetro más largo de la elipse (usualmente denotado por a). El eje mayor se extiende desde un extremo de la elipse hasta el otro en la parte más ancha y pasa por el centro.
Por otra parte, el eje menor es el diámetro más corto (denotado por b). El eje menor cruza a través del centro en la parte más angosta de la elipse.
Características principales de una elipse
Las características principales de una elipse son:
- La elipse tiene dos puntos focales, llamados los focos.
- La excentricidad de la elipse se encuentra entre [0,1].
- La suma total de cada distancia desde un punto de la elipse a los dos focos es constante.
- Las elipses tienen un eje mayor y un eje menor.
- La intersección del eje mayor y el eje menor es el centro de la elipse.
- Un círculo es un caso especial de una elipse, el cual tiene ambos focos en el centro.
Ecuación de la elipse
Dependiendo en la ubicación del centro de la elipse, podemos tener dos variaciones de su ecuación. Cuando el centro está ubicado en el origen, es decir, en el punto (0, 0), la ecuación de la elipse es:
| $latex \frac{{{x}^2}}{{{a}^2}}+\frac{{{y}^2}}{{{b}^2}}=1$ |
en donde, a representa a la longitud del semieje mayor y b representa la longitud del semieje menor.
Si es que el centro no está ubicado en el origen, la ecuación de la elipse es :
| $latex \frac{{{(x-h)}^2}}{{{a}^2}}+\frac{{{(y-k)}^2}}{{{b}^2}}=1$ |
en donde, $latex (h, k)$ es el centro de la elipse.
Véase también
¿Interesado en aprender más sobre elipses? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
