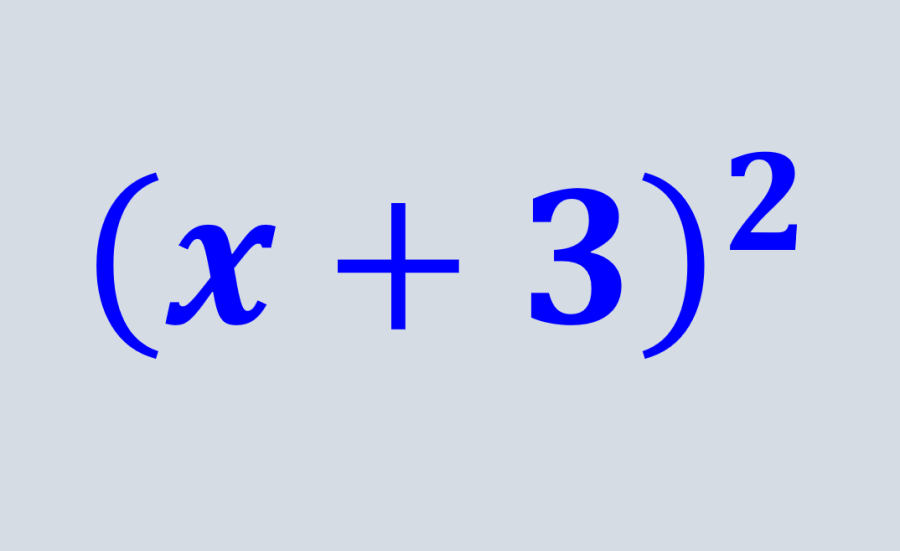En algunos casos especiales, es posible factorizar polinomios usando el trinomio cuadrado perfecto. Esta técnica nos permite factorizar este tipo de polinomios fácilmente y usar la factorización para encontrar las raíces o las soluciones a un problema.
A continuación, haremos una breve revisión del trinomio cuadrado perfecto. Veremos cómo identificar a estos trinomios y cómo aplicar esta técnica. Además, veremos varios ejercicios de trinomio cuadrado perfecto resueltos para dominar completamente el uso de esta técnica de factorización.
Resumen de trinomio cuadrado perfecto
El trinomio cuadrado perfecto es un tipo especial de factorización que puede ser usado para resolver ecuaciones algebraicas.
Recordemos que un trinomio es una expresión algebraica compuesta de tres términos que están conectados por adición o sustracción. De igual forma, un binomio es una expresión compuesta de dos términos.
Entonces, un trinomio cuadrado perfecto puede ser definido como una expresión que es obtenida al elevar al cuadrado a un binomio.
Para reconocer a un trinomio cuadrado perfecto, tomamos en cuenta lo siguiente:
- El primer y el último términos deben ser cuadrados perfectos
- El término del medio debe ser el doble del producto de las raíces cuadradas del primero y del último términos.
Una vez que hayamos identificado a un trinomio cuadrado perfecto, seguimos los siguientes pasos para factorizar:
Paso 1: Identificar los números cuadrados en el primero y último términos del trinomio.
Paso 2: Examina si es que el término del medio es positivo o negativo. Si es que el término del medio es positivo, los factores tendrán un signo más y si es que el término del medio es negativo, los factores tendrán un signo menos.
Paso 3: Escribimos los términos aplicando las siguientes identidades:
$latex {{a}^2}+2ab+{{b}^2}={{(a+b)}^2}$
$latex {{a}^2}-2ab+{{b}^2}={{(a-b)}^2}$
Ejercicios de trinomio cuadrado perfecto resueltos
Los siguientes ejercicios de trinomio cuadrado perfecto usan la técnica y los pasos detallados arriba para llegar a la solución. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Factoriza al trinomio $latex {{x}^2}+6x+9$.
Solución
Paso 1: Podemos escribir al trinomio de la siguiente forma:
$latex {{x}^2}+6x+9={{(x)}^2}+6x+{{3}^2}$
Paso 2: En este caso, el término del medio es positivo, por lo que los factores tendrán un signo más.
Paso 3: Aplicando la fórmula $latex {{a}^2}+2ab+{{b}^2}={{(a+b)}^2}$, tenemos:
$latex {{(x)}^2}+6x+{{3}^2}={{(x+3)}^2}$
EJERCICIO 2
Factoriza a la expresión $latex {{x}^2}+10x+25$.
Solución
Paso 1: Reescribimos al trinomio de la siguiente forma:
$latex {{x}^2}+10x+25={{(x)}^2}+10x+{{5}^2}$
Paso 2: Aquí, el término del medio es positivo. Esto significa que los factores tendrán un signo más.
Paso 3: Usando la fórmula $latex {{a}^2}+2ab+{{b}^2}={{(a+b)}^2}$, tenemos:
$latex {{(x)}^2}+10x+{{5}^2}={{(x+5)}^2}$
EJERCICIO 3
Factoriza el trinomio $latex {{x}^2}-8x+16$.
Solución
Paso 1: Para visualizar mejor escribimos al trinomio de la siguiente forma:
$latex {{x}^2}-8x+16={{(x)}^2}-8x+{{4}^2}$
Paso 2: El término del medio es negativo, por lo que los factores tendrán un signo menos.
Paso 3: Usando la fórmula $latex {{a}^2}-2ab+{{b}^2}={{(a-b)}^2}$, tenemos:
$latex {{(x)}^2}-8x+{{4}^2}={{(x-4)}^2}$
EJERCICIO 4
Factoriza la expresión $latex 4{{x}^2}+4x+1$.
Solución
Paso 1: Escribimos de la siguiente forma:
$latex 4{{x}^2}+4x+1={{(2x)}^2}+4x+{{1}^2}$
Paso 2: Aquí, el factor tendrá un signo más ya que el término del medio es positivo.
Paso 3: Aplicando la fórmula $latex {{a}^2}+2ab+{{b}^2}={{(a+b)}^2}$, tenemos:
$latex {{(2x)}^2}+4x+{{1}^2}={{(2x+1)}^2}$
EJERCICIO 5
Factoriza la expresión $latex 25{{y}^2}-10y+1$.
Solución
Paso 1: Reescribimos a la expresión para poder visualizar mejor:
$latex 25{{y}^2}-10y+1={{(5y)}^2}-10y+{{1}^2}$
Paso 2: Tenemos al término del medio con un signo negativo, por lo que los factores tendrán un signo menos.
Paso 3: Usando la fórmula $latex {{a}^2}-2ab+{{b}^2}={{(a-b)}^2}$, tenemos:
$latex {{(5y)}^2}-10y+{{1}^2}={{(5y-1)}^2}$
EJERCICIO 6
Factoriza la expresión $latex 9{{x}^2}+\frac{3}{2}x+\frac{1}{16}$.
Solución
Paso 1: Podemos escribir al trinomio de la siguiente forma:
$$9{{x}^2}+\frac{3}{2}x+\frac{1}{16}={{(3x)}^2}+\frac{3}{2}x+{{(\frac{1}{4})}^2}$$
Paso 2: Tenemos los factores con un signo positivo ya que el término del medio es positivo.
Paso 3: Aplicando la fórmula $latex {{a}^2}+2ab+{{b}^2}={{(a+b)}^2}$, tenemos:
$latex {{(3x)}^2}+\frac{3}{2}x+{{(\frac{1}{4})}^2}={{(x+\frac{1}{4})}^2}$
EJERCICIO 7
Factoriza la expresión $latex {{x}^4}-10{{x}^2}{{y}^2}+25{{y}^4}$.
Solución
Paso 1: Podemos escribir al trinomio de la siguiente forma:
$${{x}^4}-10{{x}^2}{{y}^2}+25{{y}^4}={{({{x}^2})}^2}+6x+{{(5{{y}^2})}^2}$$
Paso 2: Aquí, tenemos un signo positivo en el factor.
Paso 3: Aplicando la fórmula $latex {{a}^2}+2ab+{{b}^2}={{(a+b)}^2}$, tenemos:
$latex {{({{x}^2})}^2}+6x+{{(5{{y}^2})}^2}={{({{x}^2}+5{{y}^2})}^2}$
Ejercicios de trinomio cuadrado perfecto para resolver
Pon a prueba tu conocimiento sobre el trinomio cuadrado perfecto al factorizar los siguientes trinomios. Selecciona una respuesta y verifícala para comprobar que obtuviste la correcta.
Véase también
¿Interesado en aprender más sobre expresiones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
