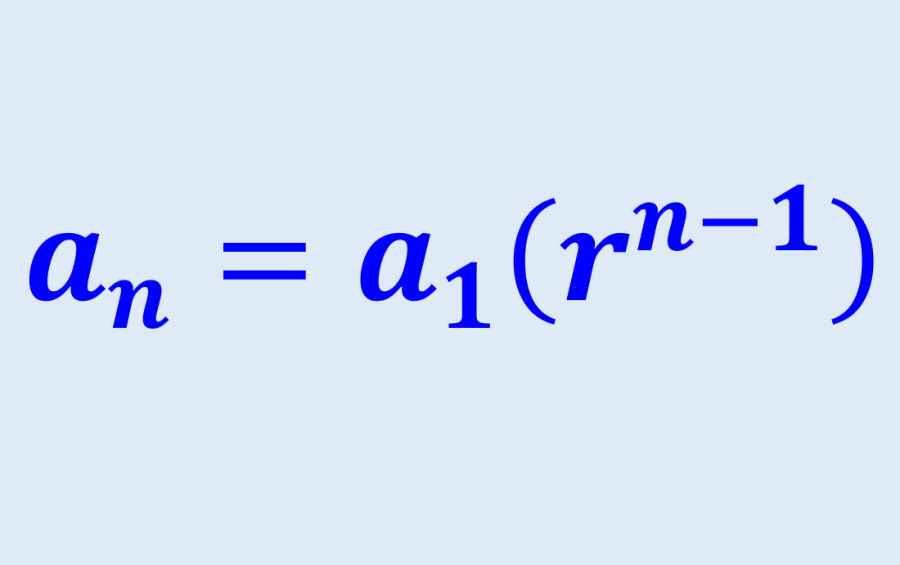Ejercicios de Sucesiones Geométricas Resueltos y para Resolver

Las sucesiones geométricas se caracterizan por tener una razón común, la cual es multiplicada por el último término para encontrar el siguiente término. Es posible encontrar cualquier término en una sucesión geométrica usando una fórmula.

A continuación, miraremos un resumen sobre las sucesiones geométricas y conoceremos su fórmula. Además, veremos varios ejercicios resueltos y ejercicios para resolver y practicar estos conceptos.

ÁLGEBRA
ejercicios de sucesiones geometricas

Relevante para…

Explorar ejercicios de sucesiones geométricas.

Ver ejercicios

ÁLGEBRA
ejercicios de sucesiones geometricas

Relevante para…

Explorar ejercicios de sucesiones geométricas.

Ver ejercicios

Resumen de sucesiones geométricas

Las sucesiones geométricas son sucesiones en las que el siguiente número en la sucesión es encontrando al multiplicar el término previo por un número llamado la razón común. La razón común es denotada por la letra r.

Dependiendo en la razón común, la sucesión geométrica puede ser creciente o decreciente. Si es que la razón común es mayor que 1, la sucesión es creciente y si es que la razón común se encuentra entre 0 y 1, la sucesión es decreciente:

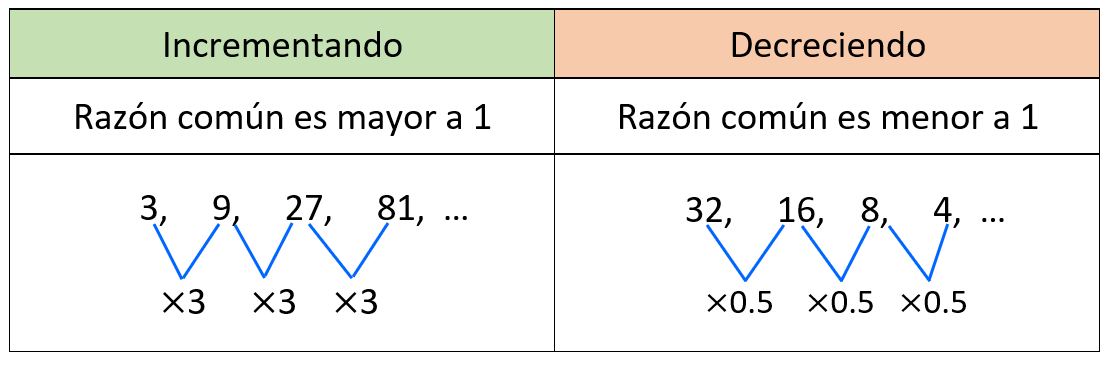
ejercicios de sucesiones geométricas

Podemos encontrar cualquier número en la sucesión geométrica usando la fórmula de la sucesión geométrica:

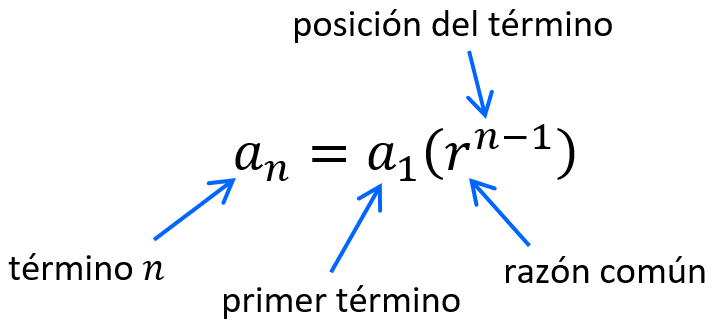
fórmula de sucesiones geométricas

Podemos encontrar la razón común al dividir un término por el término previo:

r=\frac{a_{n}}{a_{n-1}}

→ Cursos Gratis: Explora Nuestros Cursos de Matemáticas

Ejercicios de sucesiones geométricas resueltos

Los siguientes ejercicios de sucesiones geométricas tienen su respectiva solución. Las soluciones muestran el proceso a seguir paso por paso para encontrar la respuesta correcta. Es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la respuesta.

EJERCICIO 1

Encuentra el siguiente término en la sucesión geométrica: 4, 8, 16, 32, ?.

Primero, tenemos que encontrar la razón común de la sucesión geométrica. Para esto, dividimos a un término por el término previo:

  • \frac{32}{16}=2
  • \frac{16}{8}=2
  • \frac{8}{4}=2

Entonces, la razón común es 2. Para encontrar el siguiente término, multiplicamos al último término por la razón común: 32 \times 2=64.

EJERCICIO 2

¿Cuál es el siguiente término en la sucesión geométrica? 3, 15, 75, 375, ?.

Empezamos encontrando la razón común de la sucesión geométrica. Entonces, dividimos a cada término por su término previo:

  • \frac{375}{75}=5
  • \frac{75}{15}=5
  • \frac{15}{3}=5

Vemos que la razón común es 5. Encontramos el siguiente término al multiplicar al último término por la razón común: 375 \times 5=1875.

EJERCICIO 3

Determina el siguiente término en la sucesión geométrica: 48, 24, 12, 6, ?.

Nuevamente, empezamos encontrando la razón común en la sucesión:

  • \frac{6}{12}=0.5
  • \frac{12}{24}=0.5
  • \frac{24}{48}=0.5

En este caso, vemos que la razón común está entre 0 y 1, por lo que la sucesión es decreciente. El siguiente término en la sucesión geométrica es 6 \times 0.5=3.

EJERCICIO 4

Encuentra el término 12 en la sucesión geométrica: 5, 15, 45, 135, …

En este caso, tenemos que usar la fórmula de sucesiones geométricas a_{n}=a_{1}({{r}^{n-1}}). Entonces, tenemos que identificar el primer término, la razón común y la posición del término:

  • Primer término: a_{1}=5
  • Razón común: r=3
  • Posición del término: n=12

Ahora, reemplazamos estos datos en la fórmula:

a_{n}=a_{1}({{r}^{n-1}})

a_{12}=5({{3}^{12-1}})

a_{12}=5({{3}^{11}})

a_{12}=5(177147)

a_{12}=885 735

Vemos que obtuvimos un número muy grande. Las sucesiones geométricas tienden a crecer rápidamente dependiendo en la razón común.

EJERCICIO 5

Encuentra el término 8 en la sucesión geométrica 8, 32, 128, 512, …

Nuevamente, empezamos identificando al primer término, la razón común y la posición del término para usar con la fórmula:

  • Primer término: a_{1}=8
  • Razón común: r=4
  • Posición del término: n=8

Ahora, usamos la fórmula con esos valores:

a_{n}=a_{1}({{r}^{n-1}})

a_{8}=8({{4}^{8-1}})

a_{8}=8({{4}^{7}})

a_{8}=8(16384)

a_{8}=65 536

EJERCICIO 6

Encuentra el término 10 en la sucesión geométrica: 168, 84, 42, 21, …

En este caso, tenemos una sucesión geométrica decreciente por lo que esperamos que la razón común se encuentre entre 0 y 1:

  • Primer término: a_{1}=168
  • Razón común: r=0.5
  • Posición del término: n=10

Usamos la fórmula para encontrar el término 10:

a_{n}=a_{1}({{r}^{n-1}})

a_{10}=168({{0.5}^{10-1}})

a_{10}=168({{0.5}^{9}})

a_{10}=168(0.001953)

a_{10}=0.328

EJERCICIO 7

Encuentra el término 7 en la sucesión geométrica: 540, 180, 60, 20, …

Similar al ejercicio anterior, aquí tenemos una sucesión geométrica decreciente por lo que la razón común debe estar entre 0 y 1:

  • Primer término: a_{1}=540
  • Razón común: r=\frac{1}{3}
  • Posición del término: n=7

Usamos estos valores para reemplazar en la fórmula:

a_{n}=a_{1}({{r}^{n-1}})

a_{7}=540({{\left( \frac{1}{3}\right)}^{7-1}})

a_{7}=540({{\left( \frac{1}{3}\right)}^{6}})

a_{7}=540(0.0013717)

a_{7}=0.7407

Únete a nuestros cursos interactivos o practica con nuestros generadores de problemas

Ejercicios de sucesiones geométricas para resolver

Practica y pon a prueba tu conocimiento de sucesiones geométricas con los siguientes ejercicios. Selecciona una de las opciones y verifícala para saber si obtuviste la respuesta correcta.

Puedes guiarte con los ejercicios resueltos de arriba si es que tienes problemas.

Encuentra el siguiente término en la sucesión: 3, 9, 27, 81, ?.

Escoge una respuesta

¿Cuál es el siguiente término en la sucesión? 240, 120, 60, 30, ?

Escoge una respuesta

Encuentra el término 8 en la sucesión: 6, 12, 24, 48, …

Escoge una respuesta

Encuentra el término 7 en la sucesión: 540, 220, 110, 55, …

Escoge una respuesta

Encuentra el término 9 en la sucesión: 2, 6, 18, 54…

Escoge una respuesta

→ Explora más ejercicios de práctica


Véase también

¿Interesado en aprender más sobre expresiones algebraicas? Mira estas páginas:

Aprende matemáticas con nuestros recursos adicionales en varios temas diferentes

Conoce Más