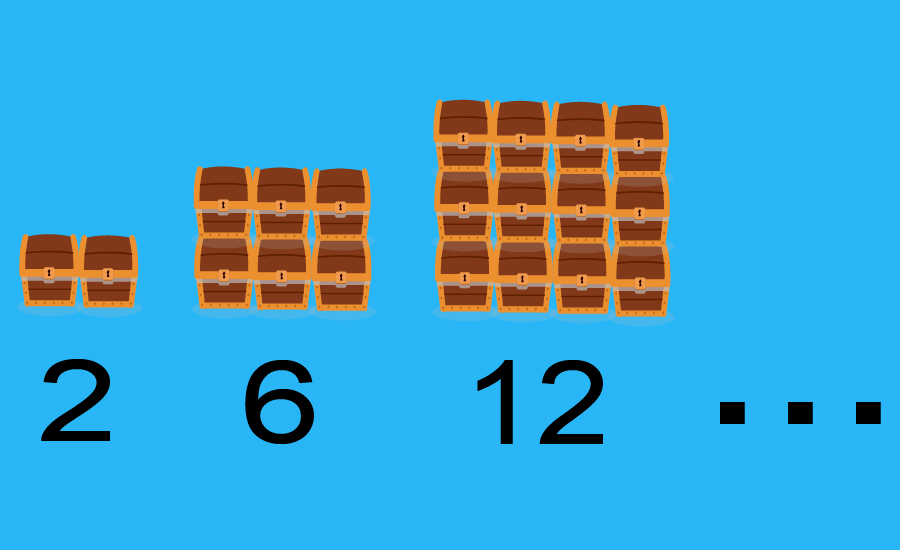Ejercicios de Sucesiones Aritméticas Resueltos y para Resolver

Los ejercicios de sucesiones aritméticas pueden ser resueltos usando la fórmula de sucesiones aritméticas. Esta fórmula nos permite encontrar cualquier número en la sucesión si es que conocemos la diferencia común, el primer término y la posición del número que queremos encontrar.

A continuación, miraremos un resumen de sucesiones aritméticas. Además, exploraremos varios ejercicios resueltos para entender la aplicación de la fórmula de sucesiones aritméticas.

ÁLGEBRA
ejercicios de sucesiones aritméticas

Relevante para…

Explorar varios ejercicios de sucesiones aritméticas.

Ver ejercicios

ÁLGEBRA
ejercicios de sucesiones aritméticas

Relevante para…

Explorar varios ejercicios de sucesiones aritméticas.

Ver ejercicios

Resumen de sucesiones aritméticas

Una sucesión aritmética es una lista de números la cual tiene un patrón definido. Podemos determinar si una sucesión es aritmética al tomar cualquier número y restarlo por el número previo. Las sucesiones aritméticas tienen una diferencia constante entre números consecutivos.

La diferencia constante entre los números consecutivos de una sucesión aritmética es denominada la diferencia común y denotada por la letra d. Si es que la diferencia común es positiva, tenemos una sucesión aritmética creciente y si es que la diferencia común es negativa, tenemos una sucesión aritmética decreciente:

ejercicios de sucesiones aritmeticas

Podemos encontrar diferentes términos de la sucesión aritmética usando la siguiente fórmula:

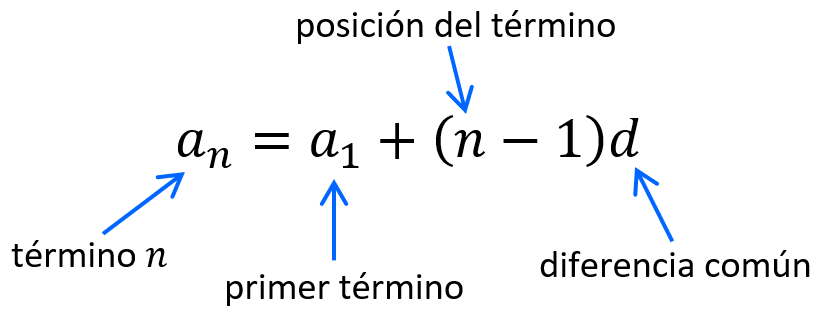
formula de sucesiones aritmeticas

Para determinar cualquier término de la sucesión aritmética, debemos conocer la diferencia común, un término en la sucesión y la posición del término que queremos determinar.

→ Cursos Gratis: Explora Nuestros Cursos de Matemáticas

Ejercicios de sucesiones aritméticas resueltos

Usando la fórmula detallada arriba, podemos resolver varios ejercicios de sucesiones aritméticas. Cada uno de los siguientes ejercicios tienen su respectiva solución detallada.

Intenta resolver los problemas tú mismo antes de mirar la solución para que puedas practicar y dominar completamente este tema.

EJERCICIO 1

Encuentra el siguiente término en la sucesión aritmética: 3, 7, 11, 15, ?.

Primero, tenemos que encontrar la diferencia común de cada par de números consecutivos:

  • 15-11=4
  • 11-7=4
  • 7-3=4

Entonces, la diferencia común es 4. Para encontrar el siguiente término después del 15, simplemente tenemos que sumar 4 al 15. Por lo tanto, tenemos 15+4=19.

EJERCICIO 2

Encuentra el siguiente término en la sucesión: 28, 23, 18, 13, ?.

Empezamos encontrando la diferencia común:

  • 13-18=-5
  • 18-23=-5
  • 23-28=-5

En este caso, obtuvimos una diferencia común negativa. Para encontrar el siguiente término, solo tenemos que sumar esta diferencia al último término. Entonces, tenemos 13+(-5)=8.

EJERCICIO 3

Encuentra los siguientes dos términos en la sucesión aritmética: -17, -13, -9, -5, ?, ?.

A primera vista, tal vez pensemos que tenemos una diferencia común negativa, ya que tenemos números negativos, pero tenemos que recordar que cuando la sucesión está creciendo, la diferencia común es positiva:

  • -5-(-9)=4
  • -9-(-13)=4
  • -13-(-17)=4

Vemos que la diferencia común es 4 positivo debido a que la sucesión geométrica está creciendo. Podemos obtener los siguientes dos términos al sumar la diferencia común al último término:

-5+4=-1

-1+4=3

EJERCICIO 4

Encuentra el término 26 en la sucesión aritmética: 3, 6, 9, 12, …

En este caso, tenemos que usar la fórmula de sucesiones aritméticas a_{n}=a_{1}+(n-1)d. Para usar esta fórmula, tenemos que conocer el primer término, la diferencia común y la posición del término que queremos encontrar:

  • Primer término: a_{1}=3
  • Diferencia común: d=3
  • Posición del término: n=26

Ahora, sustituimos estos valores en la fórmula y resolvemos:

a_{n}=a_{1}+(n-1)d

a_{26}=3+(26-1)3

a_{26}=3+(25)3

a_{26}=3+75

a_{26}=78

EJERCICIO 5

Encuentra el término 22 en la sucesión aritmética: 15, 8, 1, -6, …

Tenemos que encontrar el primer término, la diferencia común y la posición del término para reemplazar en la fórmula de sucesiones aritméticas:

  • Primer término: a_{1}=15
  • Diferencia común: d=-7
  • Posición del término n=22

Reemplazamos estos valores en la fórmula:

a_{n}=a_{1}+(n-1)d

a_{22}=15+(22-1)(-7)

a_{22}=15+(21)(-7)

a_{22}=15-147

a_{22}=132

EJERCICIO 6

Encuentra el término 16 en la sucesión aritmética: \frac{5}{2}, 3, \frac{7}{2}, 4, …

En este caso, tenemos números fraccionarios, pero similar a los problemas anteriores, solo tenemos que encontrar los diferentes valores para reemplazar en la fórmula de sucesiones aritméticas:

  • Primer término: \frac{5}{2}
  • Diferencia común: \frac{1}{2}
  • Posición del término: n=16

Ahora, usamos la fórmula con estos valores:

a_{n}=a_{1}+(n-1)d

a_{16}=\frac{5}{2}+(16-1)\frac{1}{2}

a_{16}=\frac{5}{2}+(15)\frac{1}{2}

a_{16}=\frac{5}{2}+\frac{15}{2}

a_{16}=10

Únete a nuestros cursos interactivos o practica con nuestros generadores de problemas

Ejercicios de sucesiones aritméticas para resolver

Resuelve los siguientes ejercicios de sucesiones aritméticas y pon a prueba tu conocimiento sobre este tema. Usa la fórmula de sucesiones aritméticas detallada arriba para resolver los ejercicios.

Si tienes problemas con estos ejercicios, puedes estudiar los ejercicios resueltos de arriba.

Encuentra el siguiente término en la sucesión 5, 11, 17, 23, ?.

Escoge una respuesta

Encuentra el siguiente término en la sucesión 25, 21, 17, 13, ?.

Escoge una respuesta

Encuentra el término 12 en la sucesión 1, 3, 5, 7, …

Escoge una respuesta

Encuentra el término 17 en la sucesión 4, 9, 14, 19, …

Escoge una respuesta

Encuentra el término 21 en la sucesión 18, 15, 12, 9, …

Escoge una respuesta

→ Explora más ejercicios de práctica

Véase también

¿Interesado en aprender más sobre expresiones algebraicas? Mira estas páginas:

Aprende matemáticas con nuestros recursos adicionales en varios temas diferentes

Conoce Más