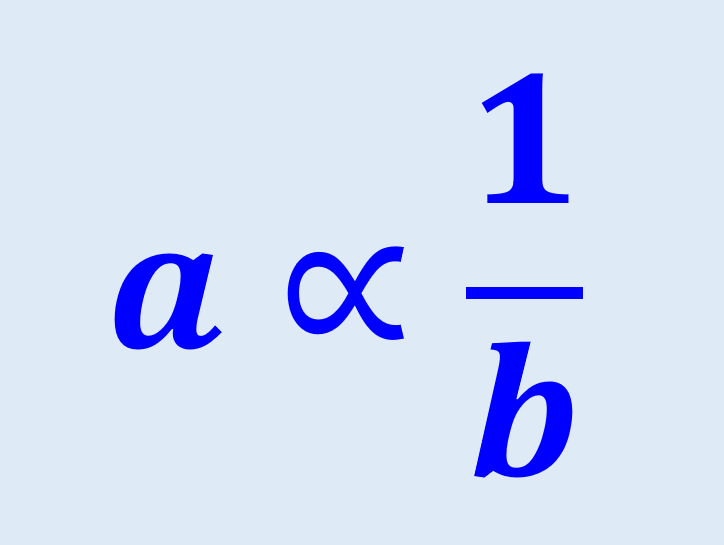La proporcionalidad es una manera de relacionar dos cantidades. En el caso de la proporcionalidad inversa, la relación es tal que, si es que incrementamos una cantidad, la otra cantidad disminuye y viceversa.
A continuación, miraremos un breve resumen de la proporcionalidad inversa para luego mirar ejercicios resueltos y entender el uso de la proporcionalidad inversa con problemas reales.
Resumen de proporcionalidad inversa
A diferencia de la proporcionalidad directa, en donde una cantidad varía directamente a medida que otra cantidad varía, en la proporcionalidad inversa, un incremento en una variable causa un decremento en la otra variable y viceversa.
Si es que la variable a es inversamente proporcional a la variable b, entonces, esto puede ser representado con la fórmula:
$latex a\propto \frac{1}{b}$
Si es que cambiamos al signo de proporcionalidad por el signo igual, tenemos la ecuación:
$latex ab=k$
en donde k es la constante de proporcionalidad.
Para encontrar una ecuación de proporcionalidad inversa, tenemos que empezar encontrando la relación proporcional. Luego, escribimos la ecuación usando la constante de proporcionalidad.
Ahora, encontramos el valor de la constante usando los valores dados y finalmente, sustituimos el valor de la constante en la ecuación.
Existen varias situaciones en la vida cotidiana que tienen relaciones de proporcionalidad inversa, por ejemplo:
- El tiempo tomado por un cierto número de trabajadores para completar un trabajo varía inversamente con respecto al número de trabajadores. Esto significa que, entre más trabajadores tengamos, menos tiempo tomará para completar el trabajo y viceversa.
- La velocidad de diferentes medios de transporte como un auto, un tren, un avión varía inversamente con respecto al tiempo tomado para viajar una cierta distancia. Entre más rápida sea la velocidad, menos tiempo tomará en cubrir una cierta distancia.
Ejercicios de proporcionalidad inversa resueltos
Los siguientes ejercicios de proporcionalidad inversa tienen su respectiva solución. Puedes usar estos ejercicios para entender completamente los conceptos de este tema. Para obtener una mejor práctica, puedes resolver los ejercicios tú mismo antes de mirar las respuestas.
EJERCICIO 1
Si es que les toma 8 días a 20 trabajadores para cultivar café en una plantación. ¿Cuánto tiempo les tomaría a 16 trabajadores para cultivar café en la misma plantación?
Solución
De la pregunta, tenemos que a 20 trabajadores les toma 8 días. Esto significa que a un trabajador le tomará:
1 trabajador $latex=(20\times 8)$ días
Ahora, calculamos el tiempo que les tomará a 16 trabajadores:
16 trabajadores $latex =\frac{20\times 8}{16}$ días
$latex =10$ días
Entonces, a 16 trabajadores les tomará 10 días.
EJERCICIO 2
9 grifos pueden llegar un tanque en 4 horas. ¿Cuánto tiempo tomaría para llenar el mismo tanque si es que tenemos 12 grifos con el mismo flujo de agua?
Solución
Les toma 4 horas a 9 grifos y tenemos que encontrar el tiempo que les toma a 12 grifos. Entonces, podemos formar la siguiente relación:
$latex \frac{x_{1}}{x_{2}}=\frac{y_{2}}{y_{1}}$
⇒ $latex \frac{9}{x}=\frac{12}{4}$
⇒ $latex x=3$
Entonces, les tomará 3 horas a 12 grifos para llenar el tanque.
EJERCICIO 3
4 personas pueden descargar un camión lleno con quintales de arroz en 3 horas. ¿Cuánto tiempo le tomaría a 7 personas para descargar el mismo camión?
Solución
Tenemos que a 4 personas les tomaría 3 horas. Esto significa que a una persona le tomará:
1 persona $latex=(4\times 3)$ horas
Ahora, calculamos el tiempo que les tomará a 7 personas:
7 personas $latex =\frac{4\times 3}{7}$ horas
$latex =\frac{12}{7}$ horas
Entonces, a 7 personas les tomará $latex \frac{12}{7}$ horas o 1.71 horas.
EJERCICIO 4
Una base militar tenía provisiones para 300 militares por 90 días. Después de 20 días, 50 militares dejaron la base. ¿Cuánto tiempo durará la comida?
Solución
Después de 20, el número de militares que quedan en la base es:
militares $latex=(300-50)=250$
Pasados los 20 días, el número de días que las provisiones durarían para los 300 militares es:
días $latex =(90-20)=70$
Entonces, 300 militares tenían provisiones para 70 días. Esto significa que 1 militar tenía provisiones para:
1 militar $latex =(300\times 70)$ días
250 militares $latex =\frac{300\times 70}{250}$ días
$latex =84$ días
Por lo tanto, las provisiones restantes durarán 84 días para 250 militares.
EJERCICIO 5
6 escritores que trabajan 5 horas diarias pueden transcribir un libro en 16 días. ¿Cuántos días les tomará a 4 escritores para transcribir el mismo libro, cada uno trabajando 6 horas diarias?
Solución
Tenemos que 6 escritores que trabajan 5 horas al día pueden terminar el trabajo en 16 días. Esto significa que 6 escritores que trabajan 1 hora al día pueden terminarlo en:
6 escritores 1 hora diaria $latex =(16\times 5)$ días
1 escritor que trabaja 1 hora al día puede terminarlo en:
1 escritor 1 hora diaria $latex =(16\times 5\times 6)$ días
1 escritor que trabaja 6 horas diarias puede terminarlo en:
1 escritor 6 horas diarias $latex =\frac{16\times 5\times 6}{6}$ días
4 escritores que trabajan 6 horas diarias pueden terminarlo en:
1 escritor 6 horas diarias $latex =\frac{16\times 5\times 6}{6\times 4}$ días
$latex =20$ días
Entonces, 4 escritores que trabajan 6 horas al día pueden terminar el trabajo en 20 días.
EJERCICIO 6
En una fábrica de juguetes, se requieren 36 máquinas para producir un cierto número de juguetes en 54 días. ¿Cuántas máquinas se necesitan para producir el mismo número de juguetes en 81 días?
Solución
Podemos formar una tabla con los datos dados:
| máquinas | 36 | x |
| días | 54 | 81 |
Ahora, podemos formar la siguiente ecuación y resolver:
$latex 36\times 54=x\times 81$
$latex \frac{36\times 54}{81}=x$
$latex \frac{4\times 54}{9}=x$
$latex x=\frac{216}{9}$
$latex x=24$
Entonces, se necesitan 24 máquinas para producir la misma cantidad de juguetes en 81 días.
Ejercicios de proporcionalidad inversa para resolver
Luego de revisar cuidadosamente los ejercicios resueltos de arriba, puedes resolver los siguientes ejercicios para poner a prueba tu conocimiento sobre proporcionalidad inversa. Selecciona una respuesta y verifícala para comprobar que escogiste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre expresiones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
