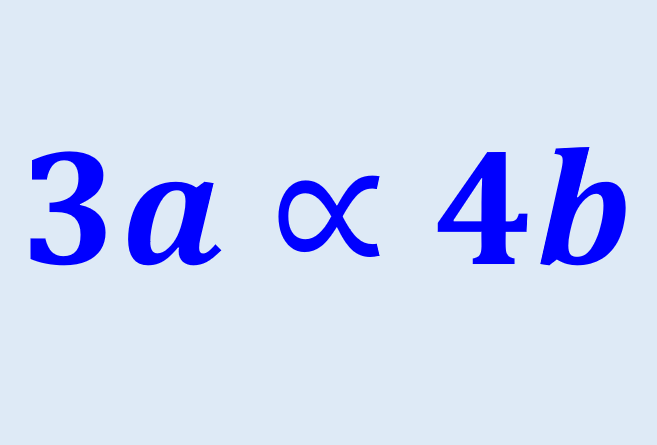La proporcionalidad nos permite relacionar dos cantidades y entender cómo cambia una cantidad si es que cambiamos la otra. Si es que dos cantidades tienen una proporcionalidad directa, entonces, cuando incrementamos una cantidad, la otra cantidad también incrementará y viceversa.
A continuación, haremos una revisión breve de la proporcionalidad directa. También veremos ejercicios de proporcionalidad resueltos y ejercicios para resolver.
Resumen de proporcionalidad directa
La proporcionalidad directa es la relación entre dos variables, las cuales tienen una razón que es igual a un valor constante. Esto significa que la proporcionalidad directa es una situación en la que un incremento en una cantidad causa un incremento correspondiente en la otra cantidad o un decremento en una cantidad resulta en un decremento en la otra cantidad.
La proporcionalidad directa está denotada por el símbolo de proporcionalidad (∝). Por ejemplo, si es que las variables a y b son proporcionales la una con la otra, podemos representar esto como a∝b. Si es que reemplazamos el signo de proporcionalidad con el signo igual, la ecuación cambia a:
$latex a=kb$
en donde k es denominada una constante de proporcionalidad.
Muchas situaciones de la vida real presentan proporcionalidades directas, por ejemplo:
- El trabajo realizado es directamente proporcional al número de trabajadores.
- El costo de la comida es directamente proporcional al peso.
- La cantidad de gasolina consumida es proporcional a la distancia viajada.
Ejercicios de proporcionalidad directa resueltos
Los siguientes ejercicios son varios problemas de aplicación de la proporcionalidad directa. Intenta resolver los ejercicios tú mismo, pero si tienes problemas, puedes mirar la solución. La solución de cada ejercicio es detallada para entender el procedimiento usado.
EJERCICIO 1
Un auto consume 12 litros de gasolina por cada 90 kilómetros viajados. ¿Qué distancia puede viajar el auto con 4 litros de gasolina?
Solución
Tenemos que el auto consume 12 litros de gasolina por cada 90 kilómetros. Entonces, por cada 1 litro de gasolina, el auto puede viajar $latex \frac{90}{12}$:
1 litro$latex =\frac{90}{12}$ km
Entonces, con 4 litros de gasolina, el auto cubre:
$latex 4\left( \frac{90}{12}\right)=30$ km
EJERCICIO 2
El costo de 6 sandías es 8 dólares. ¿Cuántas sandías pueden comprarse con 20 dólares?
Solución
La pregunta nos dice que con 8 dólares, podemos comprar 6 sandías. Entonces, con 1 dólar, podemos comprar $latex \frac{6}{8}=\frac{3}{4}$ sandías:
1 dólar$latex =\frac{3}{4}$ sandías
Por lo tanto, con 20 dólares, podemos comprar:
$latex 20\left( \frac{3}{4}\right)=15$ sandías
EJERCICIO 3
Si es que a 6 trabajadores les toma 1 mes para construir 2 casas, ¿cuántas casas construirían 9 trabajadores en 1 mes?
Solución
Aquí, la relación es solamente entre trabajadores y casas, ya que la cantidad de meses permanece igual. Tenemos que 6 trabajadores construyen 2 casas en 1 mes.
Entonces, en 1 mes, 1 trabajador construiría $latex \frac{2}{6}=\frac{1}{3}$ casas:
1 trabajador$latex =\frac{1}{3}$ casas
Por lo tanto, 9 trabajadores construirían:
$latex 9\left( \frac{1}{3}\right)=3$ casas
EJERCICIO 4
Si es que 18 vacas producen 396 litros de leche, ¿cuántas vacas se necesitarían para producir 550 litros de leche?
Solución
Tenemos que 18 vacas producen 396 litros de leche. Entonces, 1 litro de leche es producido por $latex \frac{18}{396}=\frac{1}{22}$ vacas:
1 litro$latex =\frac{1}{22}$ vacas
Por lo tanto, 550 litros son producidos por:
$latex 550\left( \frac{1}{22}\right)=25$ vacas
EJERCICIO 5
El sueldo total para 12 personas que trabajan por 6 días es 1800 dólares. ¿Cuál es el sueldo total para 20 personas que trabajan por 5 días?
Solución
Este ejercicio es similar a los anteriores, la única diferencia es que tenemos que aplicar proporcionalidad directa dos veces. Entonces, tenemos lo siguiente:
Sueldo de 12 personas por 6 días = 1800
⇒ Sueldo de 1 persona por 6 días = $latex \frac{1800}{12}=150$
⇒ Sueldo de 1 persona por 1 día = $latex \frac{150}{6}=25$
⇒ Sueldo total de 20 personas por 5 días = $latex 25 \times 20\times 5=2500$
Entonces, el sueldo total de 20 personas que trabajan por 5 días es 2500 dólares.
EJERCICIO 6
El costo para transportar 250 bultos de cementos por 120 kilómetros es 600 dólares. ¿Cuál será el costo de transportar 500 bultos por 300 kilómetros?
Solución
Similar al anterior problema, tenemos que aplicar la proporcionalidad directa dos veces. Entonces, tenemos lo siguiente:
250 bultos por 120 kilómetros = 600
⇒ 250 bultos por 1 kilómetro = $latex \frac{600}{120}=5$
⇒ 1 bulto por 1 kilómetro = $latex \frac{5}{250}=\frac{1}{50}$
⇒ 500 bultos por 300 kilómetros = $latex \frac{1}{50} \times 500\times 300=3000$
Entonces, el costo para transportar 500 bultos de cemento por 300 kilómetros es 3000 dólares.
Ejercicios de proporcionalidad directa para resolver
Usa los siguientes ejercicios de proporcionalidad directa para poner a prueba tu conocimiento sobre este tema. Selecciona una de las opciones y verifícala para comprobar que seleccionaste la respuesta correcta.
Usa los ejercicios resueltos de arriba si tienes algún problema con estos ejercicios.
Véase también
¿Interesado en aprender más sobre expresiones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
