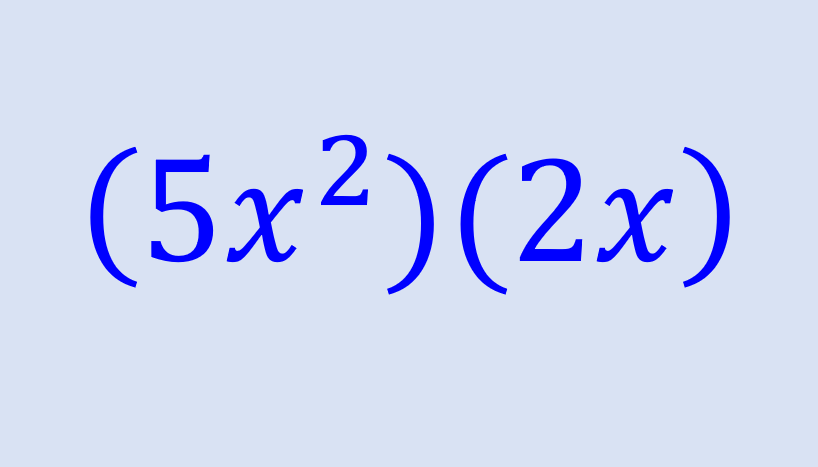Un monomio es un solo término que puede incluir cualquier combinación de números, variables, exponentes y multiplicación. Para multiplicar monomios, necesitamos estar familiarizados con las leyes de los exponentes.
A continuación, veremos un breve resumen de la multiplicación de monomios. También, exploraremos varios ejercicios resueltos que nos permitirán estudiar cuidadosamente el proceso usado para resolver ejercicios de multiplicación de monomios.
Resumen de multiplicación de monomios
Para multiplicar monomios, necesitamos entender y saber cómo aplicar las leyes de los exponentes. Veamos una revisión de las leyes de los exponentes usadas en la multiplicación de monomios:
Multiplicar potencias con la misma base
Para resolver esto, tenemos que mantener la misma base y sumar los exponentes. Por ejemplo:
$latex ({{a}^4})({{a}^3})={{a}^7}$
Potencia de una potencia
Para resolver esto, mantenemos la misma base y multiplicamos los exponentes. Por ejemplo:
$latex {{({{a}^2})}^3}={{a}^6}$
Potencia de un producto
Resolvemos la potencia de un producto al encontrar la potencia de cada factor separadamente. Por ejemplo:
$latex {{(3a)}^2}=9{{a}^2}$
Entonces, para multiplicar monomios, seguimos estos dos pasos:
Paso 1: Multiplicamos los coeficientes (números).
Paso 2: Multiplicamos las variables usando las leyes de los exponentes si es que es necesario.
Ejercicios de multiplicación de monomios resueltos
Cada uno de los siguientes ejercicios de multiplicación de monomios tiene su respectiva solución, la cual detalla el razonamiento y el proceso usados. Es recomendable intentar resolver los ejercicios antes de mirar la respuesta.
EJERCICIO 1
Multiplica los monomios $latex (4x)(3{{x}^2})$.
Solución
Paso 1: Identificamos y multiplicamos los coeficientes: los coeficientes son 4 y 3. Entonces, tenemos:
$latex 4\times 3=12$
Paso 2: Multiplicamos las variables: las variables son $latex x$ y $latex {{x}^2}$. Cuando multiplicamos dos términos con la misma base, sumamos los exponentes:
$latex (x)({{x}^2})={{x}^3}$
Ahora, combinamos las constantes y las variables:
⇒ $latex 12{{x}^3}$
EJERCICIO 2
Resuelve la multiplicación: $latex (5x)(4{{x}^3}y)$.
Solución
Paso 1: Multiplicamos a los coeficientes: los coeficientes son 5 y 4. Entonces, tenemos:
$latex 5\times 4=20$
Paso 2: Multiplicamos las variables: las variables son $latex x$ y $latex {{x}^3}$. Usamos la ley del producto de exponentes para multiplicar las variables:
$latex (x)({{x}^3})={{x}^4}$
Ahora, combinamos las constantes y las variables:
⇒ $latex 20{{x}^4}y$
En este caso, no multiplicamos a la variable y, por lo que permanece igual.
EJERCICIO 3
Multiplica los monomios $latex (5{{x}^3}y)(2{{x}^2}{{y}^5})$.
Solución
Paso 1: Empezamos multiplicando los coeficientes: los coeficientes son 5 y 2. Entonces, tenemos:
$latex 5\times 2=10$
Paso 2: Ahora, multiplicamos las variables. Tenemos que multiplicar las variables con una base x y las variables con la base y separadamente. Entonces, tenemos:
$latex ({{x}^3})({{x}^2})={{x}^5}$
$latex (y)({{y}^5})={{y}^6}$
Ahora, combinamos las constantes y las variables:
⇒ $latex 10{{x}^5}{{y}^6}$
EJERCICIO 4
Multiplica los monomios $latex (10{{x}^3}{{y}^2}{{z}^5})(-3{{x}^2}{{y}^3}z)$.
Solución
Paso 1: Tenemos que identificar y multiplicar los coeficientes: los coeficientes son 10 y -3. Entonces, tenemos:
$latex 10\times -3=-30$
Paso 2: Multiplicamos a todas las variables semejantes separadamente. Usamos la ley del producto de exponentes para obtener el resultado con cada variable:
$latex ({{x}^3})({{x}^2})={{x}^5}$
$latex ({{y}^2})({{y}^3})={{y}^5}$
$latex ({{z}^5})(z)={{z}^6}$
Combinando las constantes y las variables, tenemos:
⇒ $latex -30{{x}^5}{{y}^5}{{z}^6}$
EJERCICIO 5
Multiplica los monomios $latex (4{{x}^3}{{y}^2}z)(2{{x}^2}y{{z}^3})(3{{x}^2}{{y}^2}{{z}^2})$.
Solución
Paso 1: Empezamos multiplicando los coeficientes: los coeficientes son 4, 2 y 3. Entonces, tenemos:
$latex 4\times 2\times 3=24$
Paso 2: Tenemos las variables x, y y z. Entonces, multiplicamos cada una de las variables separadamente:
$latex ({{x}^3})({{x}^2})({{x}^2})={{x}^7}$
$latex ({{y}^2})(y)({{y}^2})={{y}^5}$
$latex (z)({{z}^3})({{z}^2})={{z}^6}$
Combinando todo esto, tenemos:
⇒ $latex 24{{x}^7}{{y}^5}{{z}^6}$
EJERCICIO 6
Resuelve la multiplicación: $latex (-3{{a}^2}{{b}^5}{{c}^3})(4{{a}^3}b{{c}^3})(-5{{a}^4}{{b}^3}{{c}^5})$.
Solución
Paso 1: Tenemos que empezar con los coeficientes: los coeficientes son -3, 4 y -5. Entonces, tenemos:
$latex -3\times 4\times -5=60$
Paso 2: Multiplicamos a las variables separadamente y usamos la ley del producto de exponentes:
$latex ({{a}^2})({{a}^3})({{a}^4})={{a}^9}$
$latex ({{b}^5})(b)({{b}^3})={{b}^9}$
$latex ({{c}^3})({{c}^3})({{c}^5})={{c}^{11}}$
Combinando todo esto, tenemos:
⇒ $latex 60{{a}^9}{{b}^9}{{c}^{11}}$
EJERCICIO 7
Resuelve la siguiente operación $latex {{(3{{x}^2}y)}^2}{{(4{{x}^2}{{y}^3})}^3}$.
Solución
En este caso, tenemos que empezar aplicando la ley de la potencia de un producto y la potencia de una potencia de exponentes para eliminar los exponentes exteriores:
$latex {{(3{{x}^2}y)}^2}{{(4{{x}^2}{{y}^3})}^3}$
⇒ $latex (9{{x}^4}{{y}^2})(64{{x}^6}{{y}^9})$
Paso 1: Ahora, tenemos que multiplicar los coeficientes: los coeficientes son 9 y 64. Entonces, tenemos:
$latex 9\times 64=576$
Paso 2: Tenemos a las variables x y y, por lo que las multiplicamos separadamente:
$latex ({{x}^4})({{x}^6})={{x}^{10}}$
$latex ({{y}^2})({{y}^9})={{y}^{11}}$
Ahora, combinamos las constantes y las variables:
⇒ $latex 576{{x}^{10}}{{y}^{11}}$
Ejercicios de multiplicación de monomios para resolver
Pon en práctica tu conocimiento sobre la multiplicación de monomios con los siguientes ejercicios. Resuelve los ejercicios y selecciona tu respuesta. Verifica la respuesta escogida para comprobar que es la correcta. Si necesitas ayuda, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre operaciones con monomios y polinomios? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
