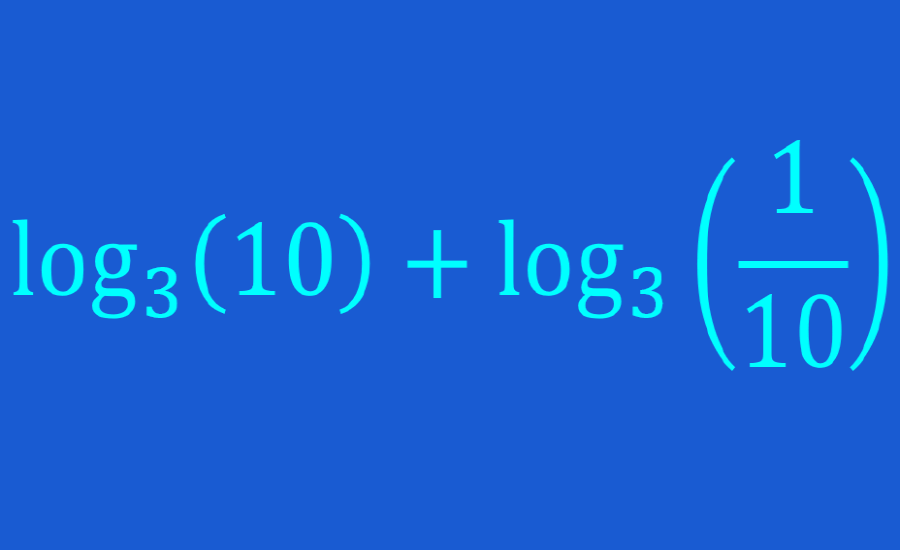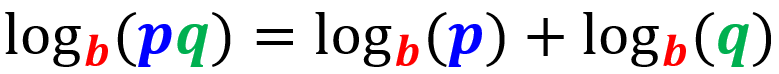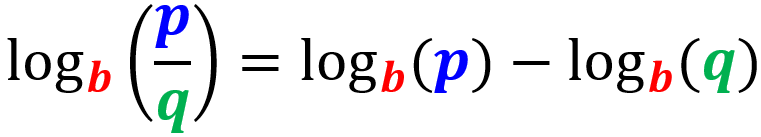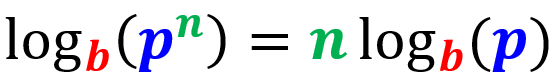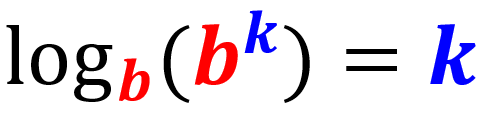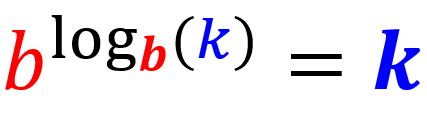Las expresiones logarítmicas pueden ser simplificadas, expandidas y resueltas usando las leyes de los logaritmos. Las leyes de los logaritmos nos indican diferentes maneras en las que una expresión logarítmica puede ser escrita.
A continuación, veremos un resumen de las principales leyes de los logaritmos. Además, veremos varios ejercicios de logaritmos resueltos para aprender cómo aplicar las leyes de los logaritmos para resolver ejercicios algebraicos.
Resumen de las leyes de los logaritmos
El logaritmo de un número es la potencia a la que el número tiene que ser elevado para obtener un valor específico. Por ejemplo, el logaritmo de base 2 de 8 es 3, ya que 2 elevado a la potencia de 3 es igual a 8:
$latex \log_{2}(8)=3$
ya que:
$latex {{2}^3}=8$
Las siguientes son las leyes de los logaritmos más importantes que nos pueden ayudar a simplificar o reescribir a las expresiones logarítmicas complejas.
Ley del producto
El logaritmo de un producto puede ser escrito como la suma de los logaritmos de los factores individuales:
Ley del cociente
El logaritmo de un cociente puede ser reescrito como el logaritmo del numerador menos el logaritmo del denominador:
Ley de la potencia
El logaritmo de una expresión exponencial puede ser reescrito como el exponente multiplicado por el logaritmo de la base (sin el exponente):
Ley del cero
El logaritmo de 1, en donde, la base es $latex b>0$, pero $latex b\neq 0$, es igual a cero:
Ley de la identidad
El logaritmo de un número igual a la base es igual a 1. Tenemos que el argumento es igual a la base, por lo que b debe ser mayor que cero, pero no puede ser igual a 1:
Ley del logaritmo del exponente
Al tomar el logaritmo de un número exponencial con la misma base del logaritmo, el resultado es el exponente:
Ley del exponente de un logaritmo
Al tener a un número elevado a logaritmo, en donde la base del logaritmo es igual a la base del número, el resultado es el argumento del logaritmo:
Ejercicios de logaritmos resueltos
Los siguientes ejercicios de logaritmos son resueltos usando las leyes de los logaritmos resumidas arriba. Cada ejercicio tiene su respectiva solución, pero es recomendable que resuelvas los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Resuelve lo siguiente: $latex \log_{4}(8)+\log_{4}(8)$.
Solución
Usando la ley del producto de logaritmos, tenemos:
$latex \log_{4}(8)+\log_{4}(8)=\log_{4}(8\times 8)$
$latex =\log_{4}(64)$
Ahora, podemos escribir al logaritmo en su forma exponencial para obtener el exponente:
$latex 64={{4}^3}$
Entonces, la respuesta es 3.
EJERCICIO 2
Resuelve la siguiente expresión: $latex \log_{5}(100)-\log_{5}(4)$.
Solución
Podemos aplicar la ley del cociente de logaritmos para formar una sola expresión con la resta de logaritmos:
$latex \log_{5}(100)-\log_{5}(4)=\log_{5}(\frac{100}{4})$
$latex =\log_{5}(25)$
Reescribiendo a la expresión en su forma exponencial, podemos encontrar el exponente:
$latex 25={{5}^2}$
Entonces, la respuesta es 2.
EJERCICIO 3
¿Cuál es el valor de $latex \log_{\sqrt{2}}(64)$?
Solución
Empezamos escribiendo al 64 como un exponencial y luego, aplicamos la ley de la potencia:
$latex \log_{\sqrt{2}}(64)=\log_{\sqrt{2}}{{(2)}^6}$
$latex =6\log_{\sqrt{2}}(2)$
Podemos escribir al 2 como un exponencial y volver a utilizar la ley de la potencia:
$latex =6\log_{\sqrt{2}}{{(\sqrt{2})}^2}$
$latex =6\times 2\log_{\sqrt{2}}(\sqrt{2})$
$latex =6\times 2(1)$
$latex =12$
EJERCICIO 4
Evalúa la siguiente expresión $$ \log_{3}(108)-2\log_{3}(2)+\log_{5}(12.5)+\log_{5}(10)$$.
Solución
Podemos simplificar esta expresión al separarla en dos partes. Vamos a simplificar los logaritmos con base 3 y los logaritmos con base 5 separadamente.
Entonces, vamos a usar la ley del cociente para simplificar los logaritmos de base 3 y vamos a usar la ley del producto para simplificar los logaritmos con base 5. Sin embargo, tenemos que empezar aplicando la ley de la potencia al logaritmo con base 3:
$$\log_{3}(108)-2\log_{3}(2)+\log_{5}(12.5)+\log_{5}(10)$$
$$=\log_{3}(108)-\log_{3}{{(2)}^2}+\log_{5}(12.5)+\log_{5}(10)$$
$$=\log_{3}(108)-\log_{3}(4)+\log_{5}(12.5)+\log_{5}(10)$$
$latex =\log_{3}(\frac{108}{4})+\log_{5}(12.5\times 10)$
$latex =\log_{3}(27)+\log_{5}(125)$
Si es que escribimos a los argumentos como potencias, podemos aplicar la ley de la potencia de logaritmos:
$latex =\log_{3}({{3}^3})+\log_{5}({{5}^3})$
$latex =3\log_{3}(3)+3\log_{5}(5)$
$latex =3(1)+3(1)$
$latex =6$
EJERCICIO 5
Simplifica la siguiente expresión $latex \log_{5}(500)-2\log_{5}(2)+\log_{6}(216)$.
Solución
Podemos aplicar la ley del producto a los logaritmos con base 5 y podemos aplicar la ley de la potencia al logaritmo de base 6:
$latex \log_{5}(500)-2\log_{5}(2)+\log_{6}(216)$
$latex =\log_{5}(500)-\log_{5}({{2}^2})+\log_{6}(216)$
$latex =\log_{5}(500)-\log_{5}(4)+\log_{6}(216)$
$latex =\log_{5}(\frac{500}{4})+\log_{6}(216)$
$latex =\log_{5}(125)+\log_{6}(216)$
Ahora, podemos reescribir a los argumentos como potencias y aplicamos la ley de la potencia de logaritmos:
$latex =\log_{5}({{5}^3})+\log_{6}({{6}^3})$
$latex =3\log_{5}(5)+3\log_{6}(1)$
$latex =3(1)+3(1)$
$latex =6$
EJERCICIO 6
Simplifica la expresión logarítmica: $latex 2\log_{3}(5)+\log_{3}(40)-3\log_{3}(10)$.
Solución
Empezamos usando la ley de la potencia para reescribir a los logaritmos. Luego, usaremos la ley del producto y la ley del cociente para formar un solo logaritmo, ya que todas las bases son las mismas:
$latex 2\log_{3}(5)+\log_{3}(40)-3\log_{3}(10)$
$latex =\log_{3}({{5}^2})+\log_{3}(40)-\log_{3}({{10}^3})$
$latex =\log_{3}(25)+\log_{3}(40)-\log_{3}(1000)$
$latex =\log_{3}(\frac{25\times 40}{1000})$
$latex =\log_{3}(1)$
Ahora, resolvemos aplicando la ley del cero:
$latex \log_{3}(1)=0$
EJERCICIO 7
¿Cuál es la versión expandida de la expresión: $latex \log_{3}(27{{x}^2}{{y}^5})$?
Solución
Tenemos un logaritmo de un producto de factores, por lo que podemos usar la ley del producto para separar los factores:
$$\log_{3}(27{{x}^2}{{y}^5})=\log_{3}(27)+\log_{3}({{x}^2})+\log_{3}({{y}^5})$$
Ahora, podemos reescribir al 27 como una potencia y aplicamos la ley de la potencia a todos los logaritmos:
$latex =\log_{3}({{3}^3})+\log_{3}({{x}^2})+\log_{3}({{y}^5})$
$latex =3\log_{3}(3)+2\log_{3}(x)+5\log_{3}(y)$
$latex =3(1)+2\log_{3}(x)+5\log_{3}(y)$
$latex =3+2\log_{3}(x)+5\log_{3}(y)$
Ejercicios de logaritmos para resolver
Pon a prueba tu conocimiento sobre los logaritmos y las leyes de los logaritmos para resolver los siguientes ejercicios. Si necesitas ayuda con estos problemas, puedes mirar las leyes de los logaritmos o los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre logaritmos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
