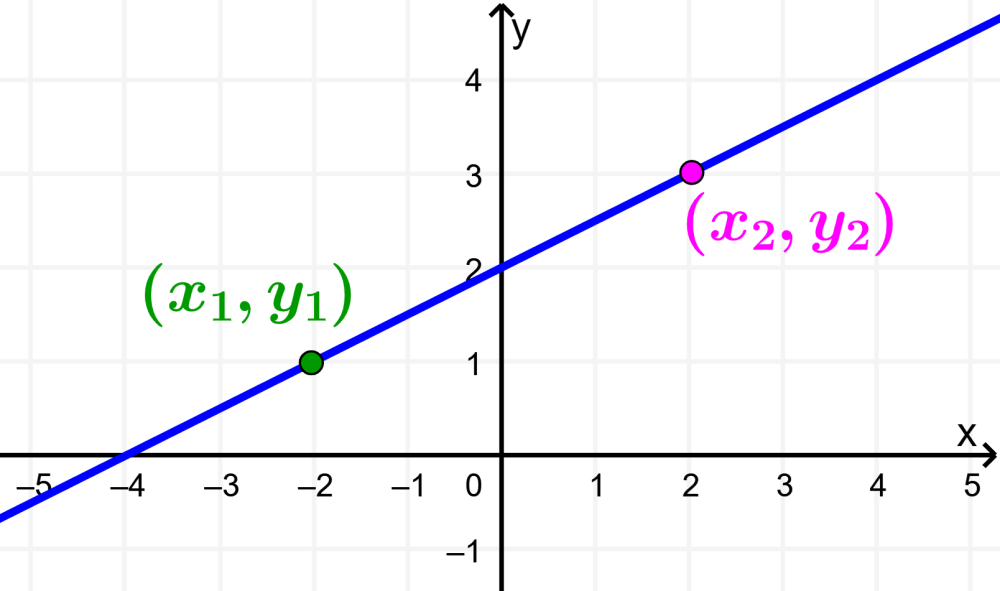
Una función lineal es definida como una función que tiene una o más variables sin exponentes. Las funciones lineales producen líneas rectas al ser graficadas. A continuación, vamos a hacer una revisión breve de las funciones lineales.
Miraremos cómo graficar funciones lineales y cómo encontrar sus ecuaciones. Además, veremos varios ejercicios resueltos para poner en práctica lo aprendido.
Resumen de funciones lineales
Una función lineal es una función que forma una línea recta al ser graficada. Este tipo de funciones son generalmente funciones polinomiales, las cuales tienen un grado máximo de 1. Una función lineal tiene una variable dependiente y una variable independiente. La variable independiente es la x y la variable dependiente es la y.
Las funciones lineales tienen la siguiente forma general:
$latex y=f(x)=mx+b$
en donde:
- b es el término constante o el intercepto en y. Este es el valor de la variable dependiente cuando tenemos $latex x=0$.
- m es el coeficiente de la variable independiente. También es conocido como la pendiente y determina la inclinación de la línea.
Graficar una función lineal
Para graficar una función lineal, seguimos los siguientes pasos:
Paso 1: Encontramos dos puntos que satisfacen la función.
Paso 2: Trazamos esos puntos en el plano cartesiano.
Paso 3: Conectamos esos puntos con una línea recta.
Encontrar la ecuación de una línea
La forma más fácil de encontrar la ecuación de una línea es escribiéndola en la forma $latex y=mx+b$.
Si es que tenemos dos puntos en una función, $latex (x_{1},~y_{1})$ y $latex (x_{2},~y_{2})$, la pendiente puede ser encontrada usando la fórmula:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
El intercepto en y es encontrado al sustituir la pendiente y usar cualquier punto para despejar para b.
Ejercicios de funciones lineales resueltos
Los siguientes ejercicios usan varios aspectos de las funciones lineales. Cada ejercicio tiene su respectiva solución, por lo que puedes mirar el razonamiento usado para llegar a la respuesta. Intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
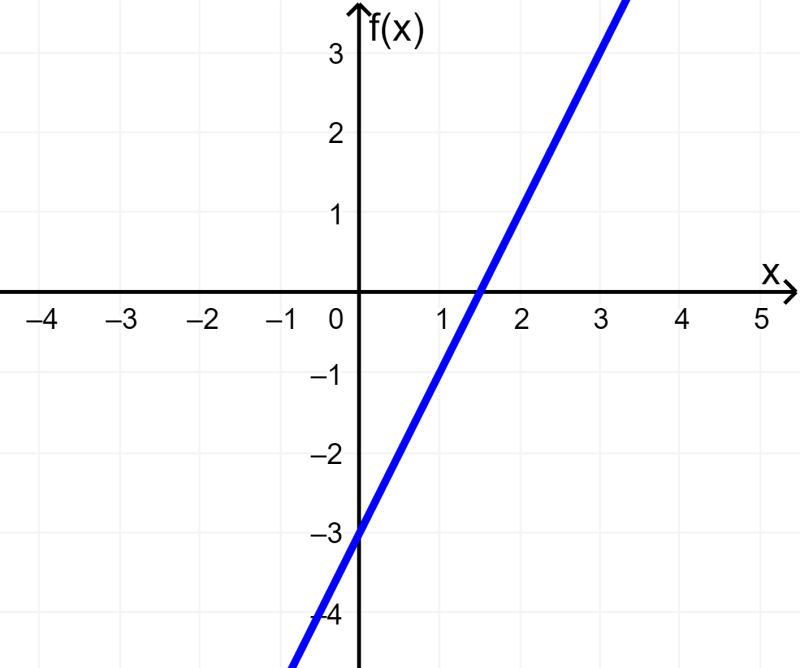
¿Representa la siguiente gráfica a una función lineal?
Solución
Fácilmente podemos determinar que la gráfica sí representa a una función lineal, ya que es una línea recta.
La gráfica representa a la función $latex f(x)=2x-3$.
EJERCICIO 2
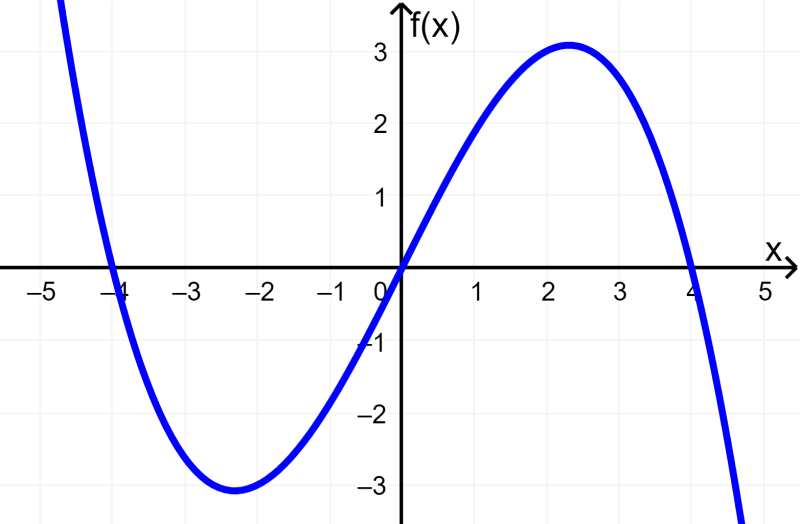
¿Es la siguiente la gráfica de una función lineal?
Solución
Esta gráfica no es una línea recta, por lo tanto no representa a una función lineal.
La gráfica representa a la función $latex f(x)=2x-\frac{1}{8}{{x}^3}$.
EJERCICIO 3
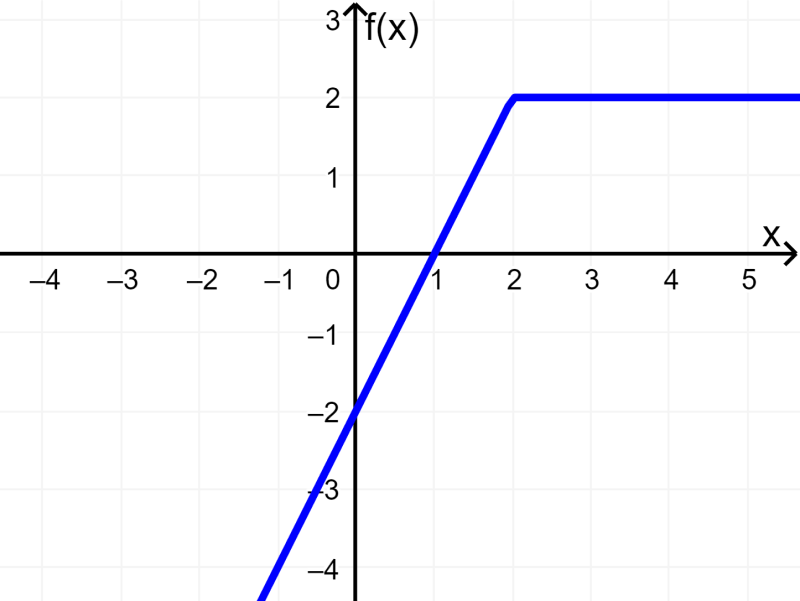
¿Repressenta la siguiente gráfica a una función lineal?
Solución
Esta función pareciera ser lineal, sin embargo, está función está compuesta de segmentos que son líneas rectas. Esta es una función definida a trozos.
La gráfica representa a la función
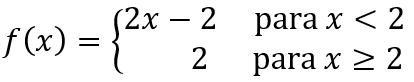
EJERCICIO 4
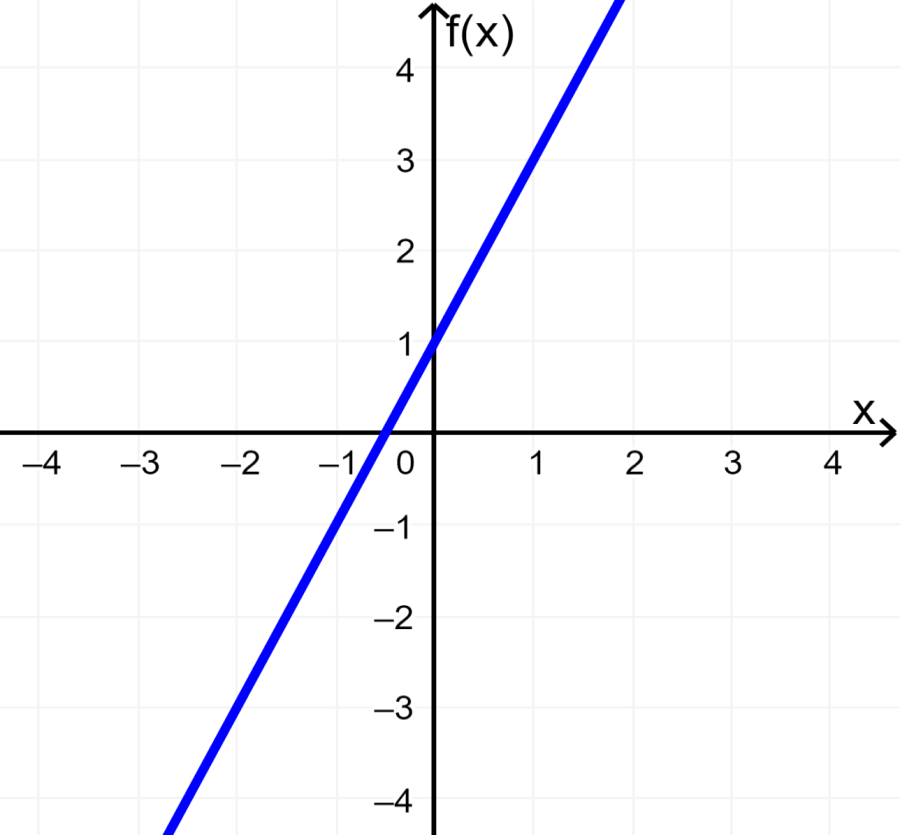
Grafica la ecuación lineal $latex f(x)=2x+1$.
Solución
Una forma de graficar esta función es al usar dos puntos que se ubican en la línea y luego trazar una línea que pase a través de los puntos. Podemos usar $latex x=0$ y $latex x=1$.
Para $latex x=0$, tenemos $latex f(0)=2(0)+1=1$. Entonces, tenemos el punto (0, 1).
Para $latex x=1$, tenemos $latex f(1)=2(1)+1=3$. Entonces, tenemos el punto (1, 3).
Graficando esos puntos y trazando una línea, tenemos:
EJERCICIO 5
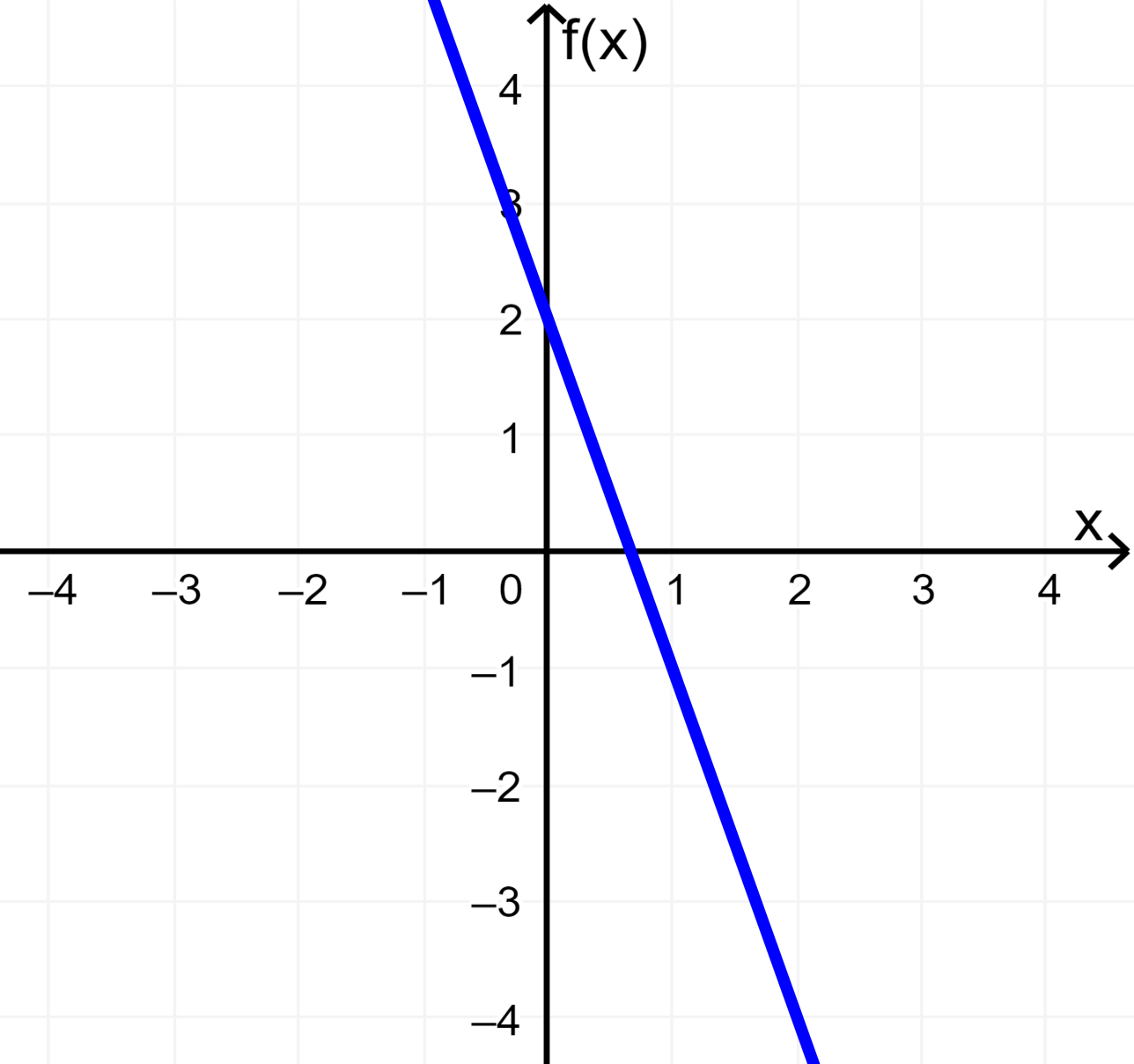
Grafica la función lineal $latex f(x)=-3x+2$.
Solución
Nuevamente, podemos encontrar dos puntos que se ubiquen en la línea. Entonces, podemos usar los valores $latex x=-1$ y $latex x=1$.
Cuando usamos $latex x=-1$, tenemos $latex f(-1)=-3(-1)+2=5$. Entonces, tenemos el punto (-1, 5).
Cuando usamos $latex x=-1$, tenemos $latex f(1)=-3(1)+2=-1$. Entonces, tenemos el punto (1, -1).
Al graficar estos puntos y trazar una línea, tenemos:
EJERCICIO 6
Encuentra la función lineal que pasa por los puntos (-2, -3) y (3, 2).
Solución
Para encontrar la ecuación de una función lineal, podemos usar la forma $latex y=mx+b$, en donde m es la pendiente y b es el intercepto en y.
La pendiente puede ser encontrada usando la fórmula $latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$. Entonces, reemplazando los valores con los dos puntos dados, tenemos:
$latex m=\frac{2-(-3)}{3-(-2)}$
$latex =\frac{5}{5}=1$
Para encontrar b, reemplazamos $latex m=1$ y usamos cualquiera de los puntos. Vamos a usar el punto (3, 2):
$latex y=mx+b$
$latex 2=1(3)+b$
$latex b=-1$
Entonces, la función lineal es $latex f(x)=x-1$.
EJERCICIO 7
Encuentra la función lineal que pasa por los puntos (-1, 4) y (2, -2).
Solución
Nuevamente, podemos usar la forma $latex y=mx+b$, en donde m es la pendiente y b es el intercepto en y.
Entonces, usamos $latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ para encontrar la pendiente con los puntos dados:
$latex m=\frac{-2-4}{2-(-1)}$
$latex =\frac{-6}{3}=-2$
Reemplazamos $latex m=-2$ para encontrar el intercepto en y, b. Vamos a usar el punto (2, -2):
$latex y=mx+b$
$latex -2=-2(2)+b$
$latex b=2$
Entonces, la función lineal es $latex f(x)=-2x+2$.
Ejercicios de funciones lineales para resolver
Pon a prueba tu conocimiento sobre funciones lineales con los siguientes ejercicios. Escoge una respuesta y verifícala para saber si seleccionaste la correcta. Usa los ejercicios resueltos de arriba si necesitas ayuda.
Véase también
¿Interesado en aprender más sobre funciones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
