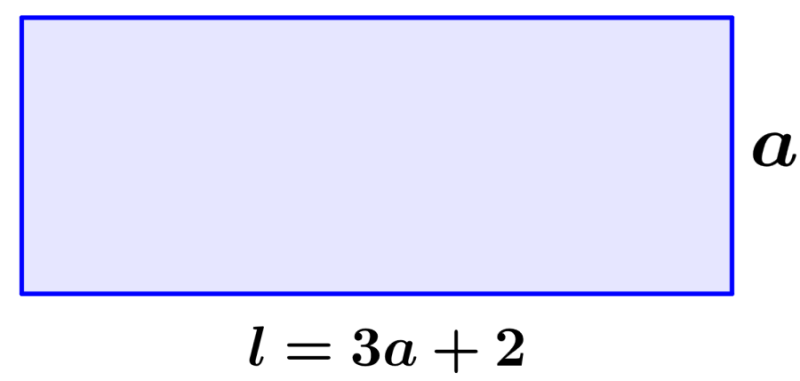Hay una gran variedad de aplicaciones de las funciones lineales. Las funciones lineales son usadas para modelar problemas de la vida real. Estos problemas son convertidos en ecuaciones matemáticas lineales que luego son resueltas usando varios métodos algebraicos.
Con las funciones lineales, podemos resolver problemas de estrategia, problemas de geometría, problemas de porcentajes y dinero y problemas de movimiento uniforme.
ÁLGEBRA
Relevante para…
Conocer algunas de las aplicaciones de las funciones lineales.
ÁLGEBRA
Relevante para…
Conocer algunas de las aplicaciones de las funciones lineales.
Aplicaciones de las funciones lineales en la vida cotidiana
Las aplicaciones de las funciones lineales en la vida cotidiana son vastas. Algunas aplicaciones comunes involucran la resolución de:
- Problemas de edades
- Problemas de velocidad, tiempo y distancia
- Problemas de geometría
- Problemas de porcentajes y dinero
- Problemas de presión y fuerzas
- Problemas de salarios
Estos problemas de la vida cotidiana son convertidos a formas matemáticas para formar ecuaciones lineales, las cuales son resueltas usando varios métodos. Estas ecuaciones deben explicar claramente la relación entre los datos y las variables.
Traducción matemática y estrategia
Las funciones lineales nos ayudan a simplificar el proceso de la resolución de problemas de la vida real. Es posible lograr esto gracias al uso de letras para representar incógnitas y valores desconocidos, transformación de los problemas verbales a ecuaciones y técnicas sistemáticas para resolver estas ecuaciones.
Para resolver problemas usando ecuaciones lineales, empezamos traduciendo los problemas verbales a formulaciones matemáticas que describen la relación entre la información dada y las incógnitas. La clave de esta traducción es leer el problema cuidadosamente e identificar ciertas palabras claves y frases. Los siguientes son ejemplos de frases clave traducidas:
| Frases clave | Traducción |
| La suma de un número y 5. | $latex x+5$ |
| Seis más que un número. | $latex x+6$ |
| Cuatro menos que un número. | $latex x-4$ |
| Siete restado de un número. | $latex x-7$ |
| El producto de cuatro y un número. | $latex 4x$ |
| Tres veces un número. | $latex 3x$ |
| Un tercio de un número. | $latex x/3$ |
| El cociente de un número y 4. | $latex x/4$ |
Problemas con relaciones entre números reales
Con las ecuaciones lineales, podemos resolver una gran variedad de problemas con números reales. Una vez que tengamos la ecuación lineal equivalente al problema verbal, podemos usar técnicas algebraicas para encontrar la respuesta al problema.
EJEMPLO
Un número entero grande es 4 menos que 3 veces un número entero pequeño. La suma de ambos números enteros es 12. Encuentra ambos números.
Solución: Empezamos identificando las variables. Entonces, asignamos una variable al número pequeño.
Vamos a usar $latex x$ para representar al número pequeño
Usamos la primera frase para identificar al número grande en términos de la variable x: “Un número entero grande es 4 menos que 3 veces un número”.
$latex 3x-4$ representa al número grande
Formamos la ecuación que representa a ambos números la cual es indicada por la segunda frase: “La suma de ambos números enteros es 12″.
$latex x+(3x-4)=12$
Ahora, resolvemos la ecuación para obtener al número pequeño x:
$latex x+(3x-4)=12$
$latex x+3x-4=12$
$latex x+3x=12+4$
$latex 4x=16$
$latex x=4$
Usamos la expresión $latex 3x-4$ para encontrar el número grande:
$latex 3(4)-4=12-4=8$
Los dos números enteros son 8 y 4.
Problemas de geometría
Varios problemas de geometría requieren el uso de ecuaciones lineales para ser resueltos. Por ejemplo, recordemos que el perímetro de un polígono es la suma de las longitudes de sus lados. Adicionalmente, recordemos algunas de las fórmulas de los perímetros:
| Figura geométrica | Perímetro |
| Cuadrado | $latex P=4l$ |
| Rectángulo | $latex P=2l+2a$ |
| Triángulo | $latex P=a+b+c$ |
| Círculo (circunferencia) | $latex P=2\pi r$ |
EJEMPLO
Un rectángulo tiene un perímetro que mide 36 metros. La longitud es 2 metros más que 3 veces el ancho. Encuentra las dimensiones del rectángulo.
Solución: La frase “La longitud es 2 metros más que 3 veces el ancho” nos da la relación entre las dos variables:
Usamos a para representar el ancho del rectángulo.
Usamos $latex 3a+2$ para representar la longitud.
La frase “Un rectángulo tiene un perímetro que mide 36 metros” nos da una ecuación algebraica. Entonces, usamos la fórmula del perímetro del rectángulo y sustituimos con la información dada:
$latex P=2l+2a$
$latex 36=2(3a+2)+2a$
Ahora que tenemos una ecuación con una variable, resolvemos para el ancho, a:
$latex 36=6a+4+2a$
$latex 36=8a+4$
$latex 32=8a$
$latex 4=a$
Usamos $latex 3x+2$ para encontrar la longitud:
$latex 3(4)+2=12+2=14$
El rectángulo mide 14 metros por 4 metros. Para verificar, sumamos todos los lados:
$latex P=14+14+4+4=36$
Problemas con porcentajes y dinero
Para resolver problemas relacionados con porcentajes, tenemos que transformar los porcentajes a decimales o fracciones. Si es que el problema nos pregunta encontrar un porcentaje, entonces, debemos recordar transformar de vuelta a porcentaje al final.
Además, si es que la pregunta involucra dinero, necesitamos asegurarnos de redondear a dos decimales.
EJEMPLO
Si es que una chaqueta cuesta 50.00 dólares incluyendo un impuesto del 8.5%, ¿cuál es el precio original antes de que los impuestos sean añadidos?
Solución: Empezamos convirtiendo 8.5% a decimal . Entonces, tenemos 0.085.
La cantidad de impuesto es igual a esta tasa multiplicada por el costo original de la chaqueta. El costo original de la chaqueta es lo que queremos encontrar.
Usamos c para representar al costo antes de añadir impuestos.
$$cantidad~de~impuesto=impuesto\times costo~de~objeto$$
$latex =0.085\times c$
$$costo~total=costo~de~objeto+cantidad~de~impuesto$$
$latex 50.00=c+0.085c$
Usamos esta ecuación para resolver para c, el costo original del objeto.
$latex 50.00=1c+0.085c$
$latex 50.00=1.085c$
$latex 46.08=c$
El costo de la chaqueta antes de impuestos es 46.08 dólares.
Problemas de movimiento uniforme
El movimiento uniforme se refiere al movimiento con una velocidad dada en donde el ritmo no cambia, es decir, no hay aceleración. Podemos determinar la distancia viajada usando una función lineal, multiplicamos la velocidad por el tiempo viajado con la fórmula $latex d=vt$.
EJEMPLO
Un auto está viajando a 50 km/h. a) Si es que viaja por 3.5 horas, ¿cuál es la distancia viajada? b) Si es que necesita viajar 350 kilómetros, ¿cuánto tiempo le tomará?
Solución: a) Usando la fórmula para la distancia $latex d=vt$, simplemente reemplazamos los datos dados en esta fórmula:
$latex d=(50)(3.5)$
$latex d=175$
Entonces, viajando a una velocidad de 50 km/h por 3.5 horas, el auto cubre una distancia de 175 km.
b) Reemplazamos los datos en la fórmula para la distancia y resolvemos para el tiempo:
$latex 350=50t$
$latex 7=t$
Entonces, viajando a una velocidad de 50 km/h, necesitamos 7 horas para cubrir una distancia de 350km.
Véase también
¿Interesado en aprender más sobre números funciones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
