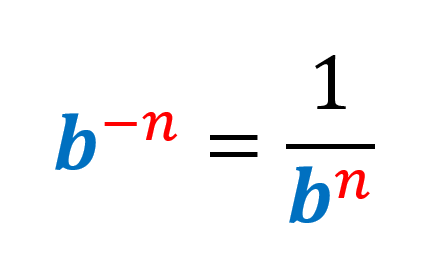Los ejercicios de exponentes negativos pueden ser resueltos al aplicar la regla de exponentes negativos, la cual nos dice que un exponente negativo puede ser transformado en positivo al tomar el recíproco de su base.
A continuación, miraremos un resumen de expresiones con exponentes negativos. Luego, veremos varios ejercicios resueltos para aprender cómo resolver este tipo de problemas. También miraremos ejercicios interactivos para poner en práctica lo aprendido.
Resumen de exponentes negativos
El exponente negativo en una expresión nos indica que debemos reescribir esta expresión al tomar el recíproco de la base y luego cambiar el signo del exponente.
Cualquier expresión que tiene exponentes negativos no es considerada como una expresión en su forma más simple. Simplemente le damos la vuelta a la fracción y convertimos el exponente negativo a exponente positivo.
Ejercicios de exponentes negativos resueltos
Los siguientes ejercicios de exponentes negativos tienen su respectiva solución para aprender el proceso usado y el razonamiento detrás de cada respuesta. Es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Simplifica la expresión $latex {{5}^{-1}}$.
Solución
La regla de exponentes negativos nos dice que $latex {{b}^{-n}}=\frac{1}{{{b}^n}}$. Entonces, tenemos que tomar el recíproco de la base y cambiar el exponente de negativo a positivo:
$latex {{5}^{-1}}=\frac{1}{{{5}^1}}$
Ahora, aplicamos el exponente para simplificar:
$latex \frac{1}{{{5}^1}}=\frac{1}{5}$
EJERCICIO 2
Simplifica la expresión $latex 3^{-3}$.
Solución
Usando la regla de exponentes negativos $latex {{b}^{-n}}=\frac{1}{{{b}^n}}$, tomamos el recíproco del 3 y cambiamos el exponente a positivo:
$latex {{3}^{-3}}=\frac{1}{{{3}^3}}$
Simplificamos al aplicar el exponente:
$latex \frac{1}{{{3}^3}}=\frac{1}{81}$
EJERCICIO 3
Simplifica la expresión algebraica $latex 2{{x}^{-4}}$.
Solución
En este caso, solo la variable está elevada a un exponente negativo, por lo que la regla de exponentes negativos solo aplica a la variable. Tomamos el recíproco de x y -4 cambia a 4:
$latex 2{{x}^{-4}}=\frac{2}{{{x}^4}}$
En este caso ya no tenemos nada para simplificar.
EJERCICIO 4
Simplifica la expresión algebraica $latex {{3}^{-2}}{{x}^{-3}}$.
Solución
Tomamos el recíproco del 3 y lo elevamos a 2 positivo y tomamos el recíproco de x y lo elevamos a 3 positivo:
$latex {{3}^{-2}} {{x}^{-3}}=\frac{1}{{{3}^2}{{x}^3}}$
Aplicamos el exponente del 3 para simplificar:
$latex \frac{1}{{{3}^2}{{x}^3}}=\frac{1}{9{{x}^3}}$
EJERCICIO 5
Simplifica la expresión algebraica $latex \frac{4x}{{{2}^{-2}}}$.
Solución
Aquí, empezamos con una fracción y un exponente negativo en el denominador. Entonces, aplicamos la regla de exponentes negativos al denominador:
$latex \frac{4x}{{{2}^{-2}}}=4x({{2}^2})$
Simplificamos al aplicar el exponente:
$latex 4x({{2}^2})=4x(4)$
$latex =16x$
EJERCICIO 6
Simplifica la expresión algebraica $latex \frac{{{x}^{-2}}}{5({{5}^{-3}})}$.
Solución
Tenemos exponentes negativos tanto en el numerador como en el denominador. Tomamos el recíproco de x y la elevamos a la potencia de 2 positivo. Tomamos el recíproco de 5 y lo elevamos a la potencia de 3 positivo:
$latex \frac{{{x}^{-2}}}{5({{5}^{-3}})}=\frac{{{5}^3}}{5{{x}^2}}$
Aplicamos el exponente y simplificamos la fracción:
$latex \frac{{{5}^3}}{5{{x}^2}}=\frac{125}{5{{x}^2}}$
$latex =\frac{25}{{{x}^2}}$
EJERCICIO 7
Simplifica la expresión algebraica $latex \frac{{{4}^{-2}}{{x}^{-5}}}{{{2}^{-5}}{{x}^{-3}}}$.
Solución
Tenemos exponentes negativos tanto en el numerador como en el denominador. Tomamos el recíproco de x y la elevamos a la potencia de 2 positivo. Tomamos el recíproco de 5 y lo elevamos a la potencia de 3 positivo:
$latex \frac{{{4}^{-2}}{{x}^{-5}}}{{{2}^{-5}}{{x}^{-3}}}=\frac{{{2}^5}{{x}^3}}{{{4}^2}{{x}^5}}$
Aplicamos los exponentes y simplificamos la fracción:
$latex \frac{{{2}^5}{{x}^3}}{{{4}^2}{{x}^5}}=\frac{32{{x}^3}}{16{{x}^5}}$
$latex =\frac{2}{{{x}^2}}$
EJERCICIO 8
Simplifica la expresión algebraica $latex \frac{{{6}^{-3}}{{y}^{-2}}}{{{3}^{-4}}{{y}^{-6}}}$.
Solución
Aplicamos la regla de exponentes negativos a todas las variables y números. Cambiamos al 6 a la y al denominador y los elevamos a la potencia de 3 positiva y 2 positiva respectivamente.
De igual forma, Cambiamos al 3 y a la y al numerador y los elevamos a la potencia de 4 positivo y 6 positivo respectivamente:
$latex \frac{{{6}^{-3}}{{y}^{-2}}}{{{3}^{-4}}{{y}^{-6}}}=\frac{{{3}^4}{{y}^6}}{{{6}^3}{{y}^2}}$
Simplificamos todo al aplicar los exponentes:
$latex \frac{{{3}^4}{{y}^6}}{{{6}^3}{{y}^2}}=\frac{81{{y}^6}}{216{{y}^2}}$
$latex =\frac{3{{y}^4}}{8}$
Ejercicios de exponentes negativos para resolver
Pon a prueba lo aprendido con los siguientes ejercicios de exponentes negativos. Resuelve los ejercicios y escoge tu respuesta. Verifica tu respuesta al hacer clic en “Verificar”.
Mira los ejercicios resueltos de arriba si tienes algún problema para resolver estos ejercicios.
Véase también
¿Interesado en aprender más sobre exponentes en expresiones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
