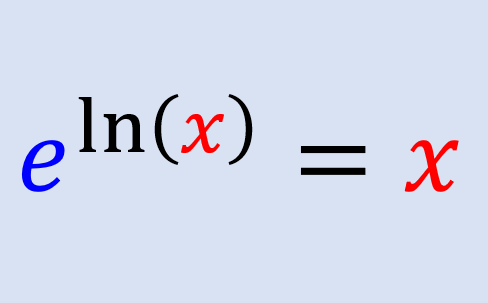Los ejercicios de ecuaciones logarítmicas pueden ser resueltos usando las leyes de los logaritmos. Con las leyes de los logaritmos, podemos reescribir a las expresiones logarítmicas para obtener expresiones más convenientes. Dependiendo del problema, podemos terminar con dos tipos de ecuaciones logarítmicas con los que tendremos que usar métodos diferentes para obtener la respuesta.
A continuación, haremos una revisión del proceso usado para resolver ejercicios de ecuaciones logarítmicas. Veremos un resumen de los dos métodos que podemos aplicar para obtener la respuesta. Además, veremos varios ejercicios resueltos para dominar completamente el tema de ecuaciones logarítmicas.
Resumen de ecuaciones logarítmicas
Las ecuaciones logarítmicas puede ser resueltas usando las leyes de los logaritmos. Estas leyes nos permiten reescribir a los logaritmos y formar expresiones más convenientes. Si necesitas revisar las leyes de los logaritmos, puedes mirar este artículo: Leyes de los Logaritmos.
El objetivo es reducir a la ecuación logarítmica hasta obtener un solo logaritmo de cada lado o un solo logaritmo en un solo lado. Basándonos en esto, podemos distinguir a dos tipos de ecuaciones logarítmicas. Tenemos que reconocer a estos dos tipos para facilitar la resolución de las ecuaciones.
Tipos de ecuaciones logarítmicas
Generalmente, luego de aplicar las leyes de los logaritmos para reducir a la ecuación, podemos terminar con uno de los dos tipos de ecuaciones logarítmicas:
- El primer tipo se ve de la siguiente manera:

En los casos en los que terminamos con un solo logaritmo en cada lado de la ecuación, podemos eliminar los logaritmos si es que tienen la misma base y podemos formar una ecuación con los argumentos. Por ejemplo, en la expresión de arriba, los argumentos son las expresiones algebraicas representadas por P y Q.
- El segundo tipo se ve de la siguiente manera:
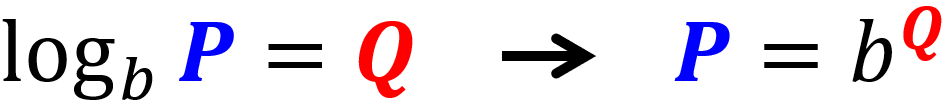
En los casos en los que terminamos con un solo logaritmo en un solo lado de la ecuación, podemos escribir al logaritmo como una expresión exponencial y resolver de esa manera.
Ejercicios de ecuaciones logarítmicas resueltos
Los siguientes ejercicios de ecuaciones logarítmicas usan las leyes de los logaritmos y ambos métodos detallados arriba. Cada ejercicio tiene su respectiva respuesta, pero es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
¿Cuál es el resultado de $latex \log_{5}(x+1)+\log_{5}(3)=\log_{5}(15)$?
Solución
Vemos que tenemos una suma de logaritmos con la misma base en el lado derecho, por lo que podemos usar la ley del producto para combinarlos. Esta es la ley del producto en caso de que no la recuerdes:
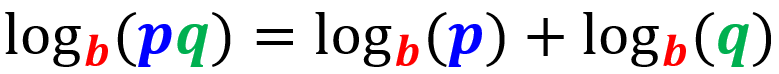
Entonces, tenemos:
$latex \log_{5}(x+1)+\log_{5}(3)=\log_{5}(15)$
$latex \log_{5}[(x+1)3]=\log_{5}(15)$
Podemos expandir la multiplicación para obtener:
$latex \log_{5}(3x+3)=\log_{5}(15)$
Los logaritmos tienen la misma base, por lo que podemos eliminarlos y formar una ecuación con los argumentos:
$latex 3x+3=15$
La ecuación lineal puede ser resuelta fácilmente:
$latex 3x+3=15$
$latex 3x=12$
$latex x=4$
EJERCICIO 2
Resuelve la ecuación $$\log_{4}(2x+2)+\log_{4}(2)=\log_{4}(x+1)+\log_{4}(3)$$.
Solución
En este caso, tenemos una suma de logaritmos en cada lado de la ecuación. Entonces, vamos a usar la ley del producto en ambos lados para obtener:
$$\log_{4}(2x+2)+\log_{4}(2)=\log_{4}(x+1)+\log_{4}(3)$$
$latex \log_{4}[(2x+2)2]=\log_{4}[(x+1)3]$
Podemos expandir la multiplicación en ambos lados para obtener:
$latex \log_{4}(4x+4)=\log_{4}(3x+3)$
Ahora, eliminamos los logaritmos y formamos una ecuación con los argumentos:
$latex 4x+4=3x+3$
La ecuación lineal puede ser resuelta fácilmente:
$latex 4x+4=3x+3$
$latex x=-1$
EJERCICIO 3
Resuelve la ecuación $$\log_{7}(x)+\log_{7}(x+5)=\log_{7}(2x+10)$$.
Solución
Podemos usar la ley del producto en la parte izquierda:
$$\log_{7}(x)+\log_{7}(x+5)=\log_{7}(2x+10)$$
$latex \log_{7}[x(x+5)]=\log_{7}(2x+10)$
Ahora, podemos distribuir la x para obtener:
$latex \log_{7}({{x}^2}+5x)=\log_{7}(2x+10)$
Podemos eliminar el logaritmo en ambos lados, ya que tienen la misma base y podemos formar una ecuación con los argumentos:
$latex {{x}^2}+5x=2x+10$
Obtuvimos una ecuación cuadrática. Podemos resolver esta ecuación al colocar a todos los términos de un solo lado y factorizar la ecuación:
$latex {{x}^2}+5x=2x+10$
$latex {{x}^2}+5x-2x-10=0$
$latex {{x}^2}+3x-10=0$
$latex (x+5)(x-2)=0$
Resolvemos para cada factor:
⇒ $latex x=-5$
⇒ $latex x=2$
Entonces, tenemos dos respuestas, $latex x=-5$ y $latex x=2$.
EJERCICIO 4
¿Cuál es el valor de x en $$\log_{3}(x+3)-\log_{3}(2)=\log_{3}(x-1)-\log_{3}(7)$$?
Solución
En este caso, tenemos restas de logaritmos en ambos lados de la ecuación, por lo que podemos aplicar la ley del cociente de logaritmos. En caso de que no la recuerde, la siguiente es la ley del cociente:
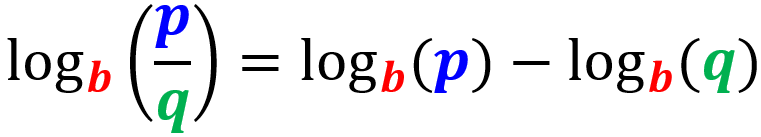
Entonces, aplicando esta ley a ambos lados, tenemos:
$$\log_{3}(x+3)-\log_{3}(2)=\log_{3}(x-1)-\log_{3}(7)$$
$latex \log_{3}(\frac{x+3}{2})=\log_{3}(\frac{x-1}{7})$
Las expresiones dentro de los logaritmos ya no pueden ser simplificadas. Sin embargo, podemos eliminar los logaritmos, ya que ambos tienen la misma base:
$latex \frac{x+3}{2}=\frac{x-1}{7}$
Podemos multiplicar en cruz para simplificar:
$latex 7(x+3)=2(x-1)$
Ahora, multiplicamos usando la propiedad distributiva:
$latex 7x+21=2x-2$
Resolvemos la ecuación lineal:
$latex 7x+21=2x-2$
$latex 5x=-23$
$latex x=-\frac{23}{5}$
EJERCICIO 5
¿Cuál es el resultado de $latex \log({{x}^2})+\frac{1}{2}\log(4)=\log({{x}^2}+16)$?
Solución
Podemos observar que los logaritmos en esta ecuación no tienen una base. Cuando tenemos logaritmos sin base, asumimos que la base es 10. Los logaritmos con base 10 son denominados logaritmos comunes.
En esta ecuación, podemos empezar usando la ley de la potencia para reescribir al logaritmo que tiene una fracción en frente. En caso de que no la recuerdes, la siguiente es la ley de la potencia:
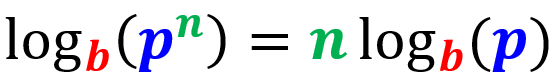
Entonces, tenemos:
$latex \log({{x}^2})+\frac{1}{2}\log(4)=\log({{x}^2}+16)$
$latex \log({{x}^2})+\log({{4}^{\frac{1}{2}}})=\log({{x}^2}+16)$
$latex \log({{x}^2})+\log(2)=\log({{x}^2}+16)$
Simplificamos el lado izquierdo usando la ley del producto:
$latex \log(2{{x}^2})=\log({{x}^2}+16)$
Podemos eliminar el logaritmo en cada lado, ya que tiene la misma base:
$latex 2{{x}^2}={{x}^2}+16$
Podemos despejar la x para resolver la ecuación cuadrática:
$latex 2{{x}^2}={{x}^2}+16$
$latex 2{{x}^2}-{{x}^2}=16$
$latex {{x}^2}=16$
Ahora, sacamos la raíz cuadrática de ambos lados:
$latex x=\sqrt{16}$
$latex x=\pm 4$
Entonces, tenemos dos respuestas, $latex x=4$ y $latex x=-4$.
EJERCICIO 6
¿Cuál es el valor de x en $latex \log(4x+60)=2$?
Solución
Aquí tampoco tenemos una base en el logaritmo, por lo que sabemos que es un logaritmo común y que su base es 10.
En esta ecuación, tenemos un logaritmo de un solo lado. Esta es una ecuación del segundo caso mencionado arriba:
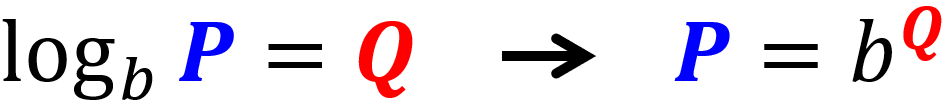
Podemos resolver esta ecuación al escribirla en su forma exponencial. Entonces, eliminamos el logaritmo de la parte izquierda y escribimos su argumento. En el lado derecho, 2 es el exponente y 10 es la base (la base del logaritmo):
$latex \log(4x+60)=2$
$latex 4x+60={{10}^2}$
Aplicamos el exponente y resolvemos la ecuación lineal:
$latex 4x+60=100$
$latex 4x=40$
$latex x=10$
EJERCICIO 7
Encuentra el valor de x en la ecuación $latex \log_{2}(3x)-2=\log_{2}(2x-5)$.
Solución
Tenemos que mover a los logaritmos a un lado de la ecuación y a los términos constantes al otro lado:
$latex \log_{2}(3x)-2=\log_{2}(2x-5)$
$latex \log_{2}(3x)-\log_{2}(2x-5)=2$
Ahora, simplificamos la parte izquierda usando la ley del cociente:
$latex \log_{2}(\frac{3x}{2x-5})=2$
Para resolver, tenemos que escribir a la ecuación en su forma exponencial. El argumento permanece en el mismo lugar y eliminamos el logaritmo. Elevamos al 2 (la base del logaritmo) al exponente 2:
$latex \frac{3x}{2x-5}={{2}^2}$
$latex \frac{3x}{2x-5}=4$
Simplificamos al multiplicar en cruz:
$latex 3x=4(2x-5)$
Distribuimos la multiplicación:
$latex 3x=8x-20$
Resolvemos la ecuación lineal:
$latex 3x=8x-20$
$latex -5x=-20$
$latex x=\frac{-20}{-5}$
$latex x=4$
→ Calculadora de Ecuaciones Logarítmicas
Ejercicios de ecuaciones logarítmicas para resolver
Pon en práctica lo aprendido sobre las ecuaciones logarítmicas con los siguientes ejercicios. Resuelve los ejercicios y escoge tu respuesta. Verifica tu respuesta para comprobar que seleccionaste la correcta.
Véase también
¿Interesado en aprender más sobre logaritmos? Mira estas páginas: