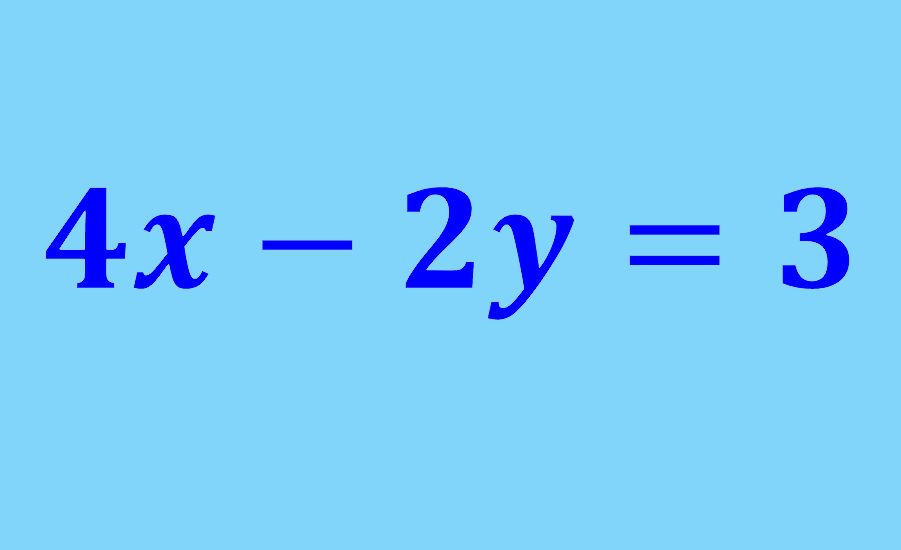Las ecuaciones lineales con dos incógnitas son ecuaciones que tienen dos variables que no están elevadas a ninguna potencia. Un ejemplo de una ecuación con dos incógnitas es x+2y=5. Estas ecuaciones solo pueden ser resueltas si es que conocemos el valor de una variable. Caso contrario, la ecuación tiene un número infinito de soluciones.
En este artículo, nos familiarizaremos con la resolución de ecuaciones lineales con dos incógnitas con ejemplos resueltos para facilitar el entendimiento de los conceptos.
Pasos para resolver ecuaciones con dos incógnitas
Los siguientes son los pasos que podemos seguir para resolver una ecuación lineal con dos incógnitas.
Si quieres aprender cómo resolver sistemas de ecuaciones con dos incógnitas, puedes visitar este artículo: Resolver Sistemas de Ecuaciones 2×2 – Métodos y Ejercicios
1. Reemplazar el valor de una variable en la ecuación.
Si conocemos el valor de una variable, lo reemplazamos en la ecuación dada. Si es que no tenemos ningún valor dado, la ecuación automáticamente tiene un número infinito de soluciones.
2. Simplificar ambos lados de la ecuación.
- Quitamos los paréntesis (usando la propiedad distributiva) si es que los hay.
- Eliminamos las fracciones (multiplicamos por el mínimo común múltiplo).
- Simplificamos los términos semejantes.
3. Aislar a la variable en un lado de la ecuación.
Realizamos operaciones para mover la variable a un lado de la ecuación y las constantes al otro lado.
4. Resolver completamente para la variable.
Por ejemplo, si tenemos $latex 4x=8$, dividimos ambos lados por 4 para obtener $latex x=2$.
5. Verificar la respuesta.
Sustituir los valores de las variables en la ecuación original para comprobar que obtenemos una ecuación correcta.
Ejercicios de ecuaciones con dos incógnitas
EJERCICIO 1
Si es que el valor de y es igual a 5, encuentra el valor de x en la ecuación $latex 3x-4y=10$.
Solución
Paso 1: Reemplazar: Tenemos que $latex y=5$, entonces, reemplazamos:
$latex 3x-4y=10$
$latex 3x-4(5)=10$
$latex 3x-20=10$
Paso 2: Simplificar: No tenemos nada para simplificar:
Paso 3: Despejar la variable: Sumamos 20 a ambos lados:
$latex 3x-20=10$
$latex 3x-20+20=10+20$
$latex 3x=30$
Paso 4: Resolvemos: Dividimos ambos lados por 3:
$$\frac{3x}{3}=\frac{30}{3}$$
$latex x=10$
EJERCICIO 2
Tenemos que el valor de y es igual a -3, resuelve la ecuación $latex -3x+5y=-6$ para x.
Solución
Paso 1: Reemplazar: Tenemos que $latex y=-3$, entonces, reemplazamos:
$latex -3x+5y=-6$
$latex -3x+5(-3)=-6$
$latex -3x-15=-6$
Paso 2: Simplificar: No tenemos términos semejantes.
Paso 3: Despejar la variable: Sumamos 15 a ambos lados:
$latex -3x-15+15=-6+15$
$latex -3x=9$
Paso 4: Resolvemos: Dividimos ambos lados por -3:
$$\frac{-3x}{-3}=\frac{9}{-3}$$
$latex x=-3$
EJERCICIO 3
Si es que tenemos $latex y=2$, encuentra el valor de $latex x$ en la ecuación $latex 2x+4y=10-x+7$.
Solución
1. Reemplazamos el valor de la variable:
$latex 2x+4(2)=10-x+7$
$latex 2x+8=10-x+7$
2. Simplificamos:
- No tenemos paréntesis.
- No tenemos fracciones.
- Combinamos términos semejantes: $latex 2x+8=17-x$.
3. Despejamos la variable: movemos el 8 hacia la derecha y el –x hacia la izquierda:
$latex 2x+8-8=17-x-8$
$latex 2x=9-x$
$latex 2x+x=9-x+x$
$latex 3x=9$
4. Despejamos completamente a la $latex x$: dividimos ambos lados por 3:
$$\frac{3}{3}x=\frac{{9}}{3}$$
$$x=\frac{{9}}{3}=3$$
5. Verificamos la respuesta: reemplazamos los valores de las variables en la ecuación original:
$latex 2(3)+4(2)=10-(3)+7$
$latex 6+8=10-3+7$
$latex 14=14$
Esto es verdadero
Respuesta: $latex y=2, x=3$.
EJERCICIO 4
Si es que tenemos $latex x=4$, encuentra el valor de $latex y$ en la ecuación $latex 5x-2y+5=12-3x+15$.
Solución
1. Reemplazamos el valor de la variable:
$$5(4)-2y+5=12-3(4)+15$$
$latex 20-2y+5=12-12+15$
2. Simplificamos:
- No tenemos paréntesis.
- No tenemos fracciones.
- Combinamos términos semejantes: $latex 25-2y=15$.
3. Despejamos la variable: movemos el 25 hacia la derecha:
$latex 25-2y-25=15-25$
$latex -2y=-10$
4. Despejamos completamente a la $latex y$: dividimos ambos lados por -2:
$$\frac{-2}{-2}y=\frac{{-10}}{-2}$$
$$y=\frac{{-10}}{-2}=5$$
5. Verificamos la respuesta: reemplazamos los valores de las variables en la ecuación original:
$$5(4)-2(5)+5=12-3(4)+15$$
$latex 20-10+5=12-12+15$
$latex 15=15$
Esto es verdadero
Respuesta: $latex y=5, x=4$.
EJERCICIO 5
Si es que el valor de x es igual a -2, resuelve la ecuación $latex 4y+2(2y+3)=3x-4$ para y.
Solución
Paso 1: Reemplazar: Tenemos que $latex x=-2$, entonces, reemplazamos:
$latex 4y+2(2y+3)=3(-2)-4$
$latex 4y+2(2y+3)=-6-4$
Paso 2: Simplificar: Expandimos el paréntesis y combinamos términos semejantes:
$latex 4y+2(2y+3)=-6-4$
$latex 4y+4y+6=-10$
$latex 8y+6=-10$
Paso 3: Despejar la variable: Restamos 6 a ambos lados:
$latex 8y+6-6=-10-6$
$latex 8y=-16$
Paso 4: Resolvemos: Dividimos ambos lados por 8:
$$\frac{8y}{8}=\frac{16}{-8}$$
$latex y=-2$
EJERCICIO 6
Encuentra el valor de $latex x$ y $latex y$ en la ecuación $latex 3x-2y=20+x$.
Solución
No tenemos ningún valor de alguna variable dado, entonces, esta ecuación tiene un número infinito de soluciones. Por ejemplo, supongamos que $latex x=1$, entonces tendríamos:
$latex 3x-2y=20+x$
$latex 3(1)-2y=20+1$
$latex 3-2y=21$
$latex -2y=21-3$
$latex -2y=18$
$latex y=-9$
Ahora, supongamos que $latex x=2$, entonces tendríamos:
$latex 3x-2y=20+x$
$latex 3(2)-2y=20+2$
$latex 6-2y=22$
$latex -2y=22-6$
$latex -2y=16$
$latex y=-8$
Podríamos seguir el proceso con diferentes valores de $latex x$ y siempre obtendríamos respuestas diferentes. Esto significa que hay un número infinito de soluciones.
EJERCICIO 7
Si es que tenemos $latex x=6$, encuentra el valor de $latex y$ en la ecuación $latex x+4(y+2)=10+2y+2x$.
Solución
1. Reemplazamos el valor de la variable:
$latex 6+4(y+2)=10+2y+2(6)$
$latex 6+4(y+2)=10+2y+12$
2. Simplificamos:
- Simplificamos paréntesis: $latex 6+4y+8=10+2y+12$.
- No tenemos fracciones.
- Combinamos términos semejantes: $latex 4y+14=2y+22$.
3. Despejamos la variable: movemos el 14 hacia la derecha y el 2y hacia la izquierda:
$latex 4y+14-14=2y+22-14$
$latex 4y=2y+8$
$latex 4y-2y=2y+8-2y$
$latex 2y=8$
4. Despejamos completamente a la $latex y$: dividimos ambos lados por 2:
$$\frac{2}{2}y=\frac{{8}}{2}$$
$$y=\frac{{8}}{2}=4$$
5. Verificamos la respuesta: reemplazamos los valores de las variables en la ecuación original:
$$6+4(4+2)=10+2(4)+2(6)$$
$latex 6+4(6)=10+8+12$
$latex 30=30$
Esto es verdadero
Respuesta: $latex y=4, x=6$
EJERCICIO 8
Si es que el valor de z es igual a 5, resuelve la ecuación $latex 4y+2z=2(3y+10)+z-11$ para y.
Solución
Paso 1: Reemplazar: Reemplazamos $latex z=5$ en la ecuación:
$latex 4y+2(5)=2(3y+10)+5-11$
$latex 4y+10=2(3y+10)+5-11$
Paso 2: Simplificar: Expandimos el paréntesis y combinamos términos semejantes:
$latex 4y+10=6y+20+5-11$
$latex 4y+10=6y+14$
Paso 3: Despejar la variable: Restamos 10 y 6y a ambos lados:
$latex 4y+10-10=6y+14-10$
$latex 4y=6y+4$
$latex 4y-6y=6y+4-6y$
$latex -2y=4$
Paso 4: Resolvemos: Dividimos ambos lados por -2:
$$\frac{-2y}{-2}=\frac{4}{-2}$$
$latex y=-2$
EJERCICIO 9
Si es que tenemos $latex y=2$, encuentra el valor de $latex x$ en la ecuación $latex \frac{1}{3}x+2y+\frac{1}{2}x=y+x+1$.
Solución
1. Reemplazamos el valor de la variable:
$$\frac{1}{3}x+2(2)+\frac{1}{2}x=2+x+1$$
$$\frac{1}{3}x+4+\frac{1}{2}x=2+x+1$$
2. Simplificamos:
- No tenemos paréntesis.
- Simplificamos fracciones: multiplicamos por 6: $latex 2x+24+3x=12+6x+6$.
- Combinamos términos semejantes: $latex 5x+24=18+6x$.
3. Despejamos la variable: movemos el 24 hacia la derecha y el 6x hacia la izquierda:
$latex 5x+24-24=18+6x-24$
$latex 5x=6x-6$
$latex 5x-6x=6x-6-6x$
$latex -x=-6$
4. Despejamos completamente a la $latex x$: dividimos ambos lados por -1:
$$\frac{-1}{-1}x=\frac{{-6}}{-1}$$
$$x=\frac{{-6}}{-1}=6$$
5. Verificamos la respuesta: reemplazamos los valores de las variables en la ecuación original:
$$\frac{1}{3}(6)+2(2)+\frac{1}{2}(6)=(2)+(6)+1$$
$latex 2+4+3=2+6+1$
$latex 9=9$
Esto es verdadero
Respuesta: $latex y=2, x=6$
EJERCICIO 10
Si es que el valor de y es igual a -3, resuelve la ecuación $latex \frac{y+1}{2}+2x=2(2y+6)+x+2$ para x.
Solución
Paso 1: Reemplazar: Tenemos que $latex y=-3$, entonces, reemplazamos:
$$\frac{-3+1}{2}+2x=2(2(-3)+6)+x+2$$
$$\frac{-3+1}{2}+2x=2(-6+6)+x+2$$
Paso 2: Simplificar: Combinamos términos semejantes y simplificamos:
$$\frac{-2}{2}+2x=2(0)+x+2$$
$latex -1+2x=x+2$
Paso 3: Despejar la variable: Sumamos 1 y restamos x a ambos lados:
$latex -1+2x+1=x+2+1$
$latex 2x=x+3$
$latex 2x-x=x+3-x$
$latex x=3$
Paso 4: Resolvemos: Ya no tenemos que dividir:
$latex x=3$
EJERCICIO 11
Resuelve la ecuación $latex 2x+2y=3x+10$ para y.
Solución
Paso 1: Reemplazar: En este caso no tenemos ningún valor dado, por lo que automáticamente, la ecuación tiene un número infinito de soluciones. Por ejemplo, supongamos que tenemos $latex x=0$, entonces, tendríamos:
$latex 2x+2y=3x+10$
$latex 2(0)+2y=3(0)+10$
$latex 2y=10$
$latex y=5$
Si es que ahora tenemos $latex x=1$, tenemos:
$latex 2x+2y=3x+10$
$latex 2(1)+2y=3(1)+10$
$latex 2+2y=3+10$
$latex 2+2y=13$
$latex 2y=15$
$latex y=15/2$
Podríamos seguir con diferentes valores y cada vez obtendríamos resultados diferentes, por lo que al no tener un valor especificado de una variable, la ecuación tiene infinitas soluciones.
Ejercicios de práctica de ecuaciones lineares con dos incógnitas
Si es que x=7, ¿cuál es el valor de y en $latex 4(x+8)-2y=3y+10$?
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre ecuaciones? Mira estas páginas: