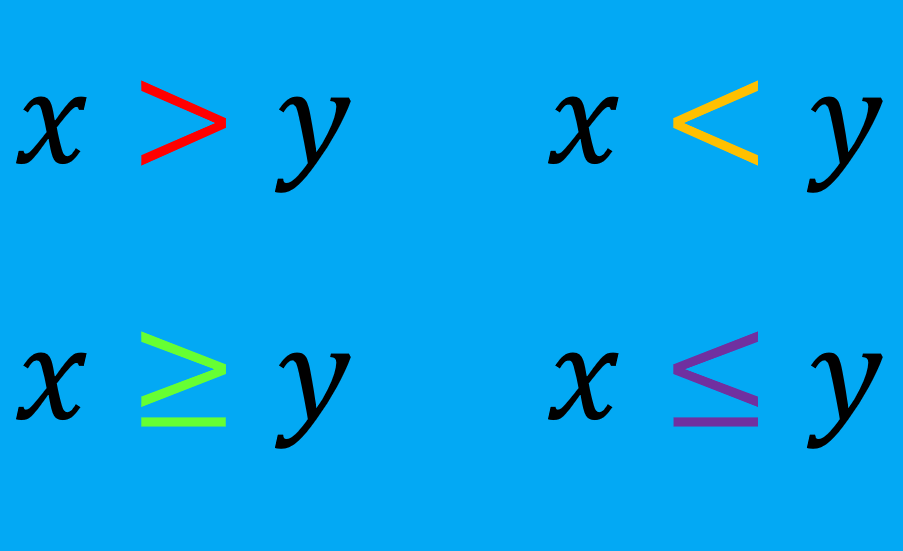Ejercicios de Desigualdades Lineales Resueltos

• Empezamos escribiendo el problema original:

$latex 3x-5>1$

• Para despejar la variable, sumamos 5 a mbos lados de la desigualdad:

$latex 3x-5+5>1+5$

• Luego de simplificar, la expresión se reduce a:

$latex 3x>6$

• Para resolver, dividimos ambos lados por 3:

$latex \frac{3}{3}x> \frac{6}{3}$

$latex x> 2$

• Graficamos la desigualdad con un punto abierto, ya que el 2 no está incluido en la solución. La solución es todos los números hacia la derecha del 2:

Paso 1: Aquí, no tenemos nada para simplificar, por lo que empezamos con:

$latex 5x-10<15$

Paso 2: Para despejar la variable, sumamos 10 de ambos lados y simplificamos:

$latex 5x-10+10<15+10$

$latex 5x<25$

Paso 3: Para resolver, dividimos ambos lados por 5:

$latex \frac{5}{5}x<\frac{25}{5}$

$latex x<5$

Paso 4: Para graficar, notamos que las soluciones a la desigualdad son todos los números reales hacia la izquierda de 5. El 5 no está incluido, por lo que usamos un punto vacío para indicar esto:

Paso 1: No tenemos nada que simplificar, por lo que empezamos con:

$latex -4x-5\leq 3$

Paso 2: Sumamos 5 a ambos lados para despejar la variable:

$latex -4x-5+5\leq 3+5$

$latex -4x\leq 8$

Paso 3: Dividimos ambos lados por -4 para obtener:

$latex \frac{-4}{-4}x\leq\frac{8}{-4}$

$latex x\geq -2$

Paso 4: En este caso, -2 sí es parte de la solución. Entonces, usamos un punto sólido para indicar que las soluciones son todos los números hacia la derecha del -2, incluido el -2:

En este caso, tenemos variables en ambos lados. Tenemos que mover las variables a un solo lado y las constantes al otro. No importa cuál lado contenga las variables, pero es estándar mover las variables a la izquierda:

• Empezamos con el problema original:

$latex 4x+2\geq 2x+10$

• Restamos 2 y 2x de ambos lados para despejar la variable:

$$4x+2-2-2x\geq 2x+10-2-2x$$

• Simplificando la desigualdad, tenemos:

$latex 2x\geq 8$

• Dividimos ambos lados por 2 y simplificamos para obtener la respuesta:

$latex \frac{2}{2}x\geq \frac{8}{2}$

$latex x\geq 4$

• Aquí, el 4 sí es parte de la solución, por lo que usamos un punto cerrado para indicar esto:

Paso 1: No tenemos nada para simplificar. Empezamos con la desigualdad:

$latex 5x+3>3x-3$

Paso 2: Restamos 3 y 3x de ambos lados para despejar la variable:

$latex 5x+3-3-3x>3x-3-3-3x$

$latex 2x>-6$

Paso 3: Dividimos ambos lados por 2 para resolver:

$latex \frac{2}{2}x>\frac{-6}{2}$

$latex x>-3$

Paso 1: Tenemos paréntesis, por lo que aplicamos la propiedad distributiva para eliminarlos:

$latex 3(x+2)>-9$

$latex 3x+6>-9$

Paso 2: Para despejar la variable, restamos 6 a ambos lados:

$latex 3x+6-6>-9-6$

$latex 3x>-15$

Paso 3: Para resolver, dividimos ambos lados por 3:

$latex \frac{3}{3}x>\frac{-15}{3}$

$latex x>-5$

En este caso, tenemos paréntesis, por lo que usamos la propiedad distributiva para eliminar paréntesis y simplificar:

• Escribimos el problema original:

$latex 2(3x-3)>4x$

• Aplicamos la propiedad distributiva:

$latex 2(3x)+2(-3)>4x$

$latex 6x-6>4x$

• Sumamos 6 de ambos lados y restamos 4x para despejar la variable:

$latex 6x-6+6-4x>4x+6-4x$

• Luego de simplificar, la expresión se reduce a:

$latex 2x>6$

• Al dividir ambos lados por 2, tenemos:

$latex \frac{2}{2}x> \frac{6}{2}$

$latex x> 3$

Paso 1: Simplificamos el paréntesis y combinamos términos semejantes:

$latex 2(2x+4)+5>1$

$latex 4x+8+5>1$

$latex 4x+13>1$

Paso 2: Despejamos la variable al restar 13 de ambos lados:

$latex 4x+13-13>1-13$

$latex 4x>-12$

Paso 3: Tenemos que dividir por 4:

$latex \frac{4}{4}x>\frac{-12}{4}$

$latex x>-3$

Paso 1: Simplificamos los paréntesis de ambos lados y combinamos términos semejantes:

$latex 4(2x+4)-3\leq 2(3x+4)+3$

$latex 8x+16-3\leq 6x+8+3$

$latex 8x+13\leq 6x+11$

Paso 2: Restamos 13 y 6x de ambos lados para despejar la variable:

$$8x+13-13-6x\leq 6x+11-13-6x$$

$latex 2x\leq -2$

Paso 3: Para resolver, dividimos ambos lados por 2:

$latex \frac{2}{2}x\leq \frac{-2}{2}$

$latex x\leq -1$

Paso 1: Simplificamos los paréntesis de ambos lados y combinamos términos semejantes:

$latex 2(x+5)-10\geq 4(2x+6)$

$latex 2x+10-10\geq 8x+24$

$latex 2x\geq 8x+24$

Paso 2: Restamos ambos lados por 8x para despejar la x:

$latex 2x-8x\geq 8x+24-8x$

$latex -6x\geq 24$

Paso 3: Ahora, dividimos por -6:

$latex \frac{-6}{-6}x\geq\frac{24}{-6}$

$latex x\leq -4$