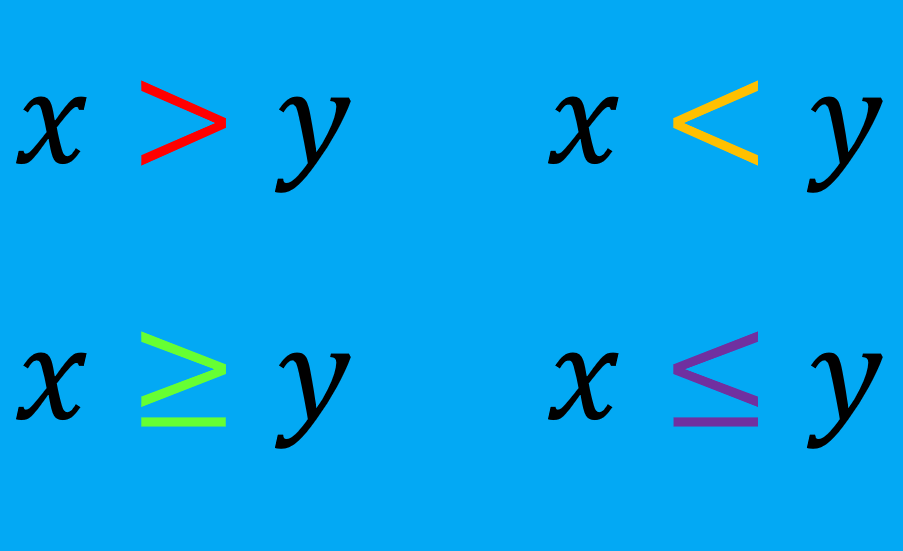¿Cómo Resolver Desigualdades Lineales?

El proceso para resolver desigualdades lineales en una variable es similar a resolver ecuaciones básicas. La mayoría de las reglas o técnicas usadas para resolver ecuaciones pueden ser fácilmente usadas para resolver desigualdades. La única diferencia importante es como el símbolo de desigualdad cambia dirección cuando un número negativo es multiplicado o dividido a ambos lados de una ecuación.

A continuación, miraremos ejercicios resueltos para dominar el proceso de resolución de desigualdades lineales.

ÁLGEBRA

Relevante para…

Aprender a resolver desigualdades lineales.

Ver ejercicios

Contenidos

ÁLGEBRA

Relevante para…

Aprender a resolver desigualdades lineales.

Ver ejercicios

Símbolos de desigualdad con ilustraciones

Los siguientes son los símbolos usados para representar desigualdades:

Mayor que

Símbolo:

Ejemplo: x es mayor que -2:

Gráfica:

Menor que

Símbolo:

Ejemplo: x es menor que 4:

Gráfica:

Mayor o igual que

Símbolo:

Ejemplo: x es mayor o igual que -3:

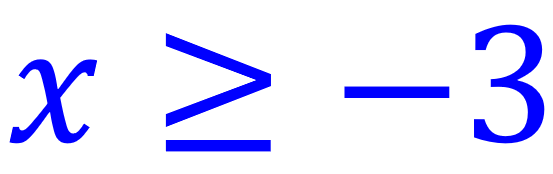
ejemplo de desigualdad con mayor o igual que

Gráfica:

grafica de desigualdad mayor o igual que

Menor o igual que

Símbolo:

Ejemplo: x es menor o igual que 3:

ejemplo de desigualdad con menor o igual que

Gráfica:

grafica de desigualdad menor o igual que

→ Cursos Gratis: Explora Nuestros Cursos de Matemáticas

Desigualdades lineales ejemplos resueltos

Los siguientes ejemplos resueltos nos permitirán dominar completamente el proceso de resolución de desigualdades lineales. Intenta resolver los ejercicios tú mismo antes de mirar la solución.

EJEMPLO 1

Resuelve y grafica la solución de la desigualdad $4x-6>2$ .

Solución

Para resolver la desigualdad, queremos encontrar todos los valores de x que la satisfacen. Esto significa que hay un número infinito de soluciones las cuales al ser sustituidas, harían que la desigualdad sea verdadera. Entonces, seguimos los siguientes pasos:

Escribimos el problema original:

$4x-6>2$

Sumamos 6 a ambos lados para mantener las variables de un lado y las constantes del otro:

$4x-6+6>2+6$

Luego de simplificar, la expresión se reduce a:

$4x>8$

Dividimos ambos lados por 4 y simplificamos para obtener la respuesta:

$\frac{4}{4}x>\frac{8}{4}$

$x>2$

Usamos un punto abierto para indicar que el 2 no es parte de la solución. La solución a la desigualdad incluye todos los valores hacia la derecha del 2, pero no incluye al 2:

EJEMPLO 2

Resuelve y grafica la desigualdad $-2x-3\geq 1$ .

Solución

Este es un ejemplo de lo que sucede con la desigualdad cuando dividimos por un número negativo:

Escribimos el problema original:

$-2x-3\geq 1$

Despejamos a la variable al sumar 3 a ambos lados:

$-2x-3+3\geq 1+3$

Luego de simplificar, la expresión se reduce a:

$-2x\geq 4$

Dividimos ambos lados por -2 y simplificamos para obtener la respuesta:

$\frac{-2}{-2}x\geq \frac{4}{-2}$

$x\leq -2$

Siempre recuerda cambiar la dirección de la desigualdad al dividir o multiplicar por un número negativo.

Usamos un punto cerrado para indicar que el -2 sí es parte de la solución. La solución a la desigualdad incluye al -2 y todos los valores hacia la izquierda:

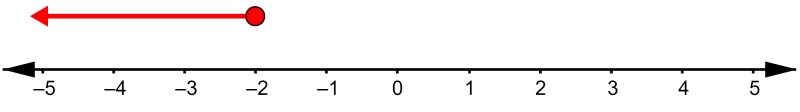
EJEMPLO 3

Resuelve la desigualdad $5-3x>13-5x$ .

Solución

Aquí tenemos variables en ambos lados. Es posible despejar las variables al lado izquierdo o al lado derecho, pero lo estándar es hacerlo al lado izquierdo.

Escribimos el problema original:

$5-3x>13-5x$

Podemos sumar 5x a ambos lados y restar 5 para despejar la variable:

$5-3x+5x-5>13-5x+5x-5$

Simplificando la expresión, tenemos:

$2x>8$

Podemos obtener la respuesta al dividir ambos lados por 2:

$\frac{2}{2}x> \frac{8}{2}$

$x> 2$

EJEMPLO 4

Resuelve la desigualdad $2(2x+3)<2x+12$ .

Solución

En este caso, tenemos paréntesis, por lo que tenemos que empezar aplicando la propiedad distributiva para eliminar los paréntesis:

Escribimos el problema original:

$2(2x+3)<2x+12$

Aplicamos la propiedad distributiva:

$2(2x)+2(3)<2x+12$

$6x+6<2x+12$

Despejamos a la variable al restar 6 y 2x a ambos lados:

$6x+6-2x-6<2x+12-2x-6$

Luego de simplificar, la expresión se reduce a:

$4x<8$

Dividimos ambos lados por 4 y simplificamos para obtener la respuesta:

$\frac{4}{4}x< \frac{8}{4}$

$x< 2$

EJEMPLO 5

Resuelve la desigualdad $2(3x-4)\geq 7x-7$ .

Solución

Nuevamente, empezamos aplicando la propiedad distributiva para eliminar el paréntesis:

Escribimos el problema original:

$2(3x-4)\geq 7x-7$

Aplicamos la propiedad distributiva:

$2(3x)+2(-4)\geq 7x-7$

$6x-8\geq 7x-7$

Ahora, sumamos 8 y restamos 7x de ambos lados para despejar la variable:

$6x-8+8-7x\geq 7x-7+8-7x$

Simplificamos para obtener:

$-x\geq 1$

Dividimos ambos lados por -1 y simplificamos para obtener la respuesta:

$\frac{-1}{-1}x\geq \frac{1}{-1}$

$x\geq -1$

EJEMPLO 6

Resuelve la desigualdad $3(x+2)+2\leq 2(x-1)+8$ .

Solución

En este caso, tenemos que aplicar la propiedad distributiva a ambos paréntesis y luego combinamos términos semejantes para simplificar:

Escribimos el problema original:

$3(x+2)+2\leq 2(x-1)+8$

Aplicamos la propiedad distributiva a ambos paréntesis:

$3(x)+3(2)+2\leq 2(x)+2(-1)+8$

$3x+6+2\leq 2x-2+8$

Combinamos términos semejantes para simplificar:

$3x+8\leq 2x+6$

Despejamos a la variable al restar 8 y 2x a ambos lados:

$3x+8-8-2x\leq 2x+6-8-2x$

Simplificando, tenemos:

$x\leq -2$

Ya no tenemos que dividir:

$x\leq -2$

Únete a nuestros cursos interactivos o practica con nuestros generadores de problemas

Desigualdades lineales ejercicios para resolver

Pon a prueba tus habilidades y tu conocimiento sobre desigualdades lineales con los siguientes ejercicios interactivos. Escoge una respuesta y verifícala para comprobar que seleccionaste la respuesta correcta.

Los ejercicios resueltos de arriba pueden servir de guía si tienes problemas con estos ejercicios.