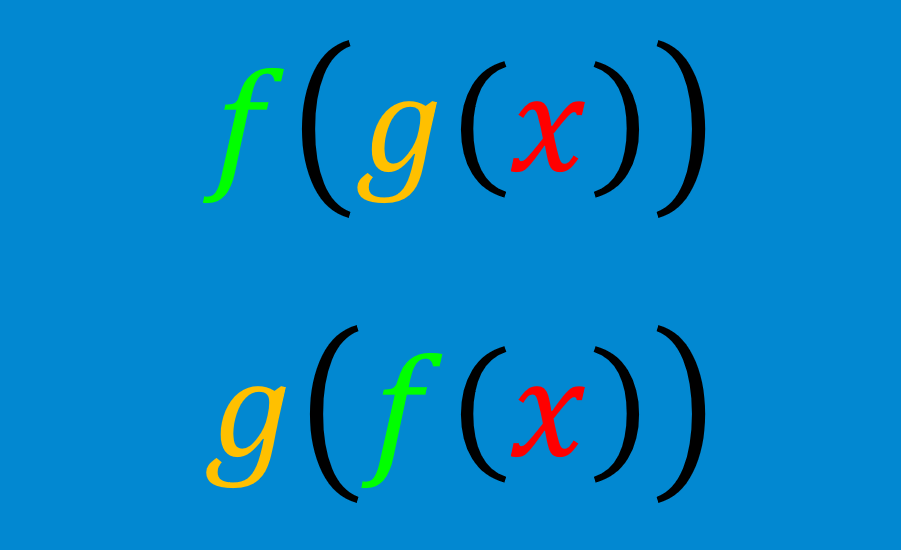Una composición de funciones es formada al tomar las salidas de una función y convertirlas en las entradas de otra función. Estas funciones pueden resultar muy útiles cuando tenemos que modelar diferentes procesos con distintas funciones.
A continuación, exploraremos un resumen breve sobre la composición de funciones y sobre cómo obtener la composición si es que tenemos dos funciones. Además, veremos varios ejercicios resueltos para dominar el proceso usado para obtener la composición de funciones.
Resumen de composición de funciones
La composición de funciones es una operación en donde dos funciones como $latex f(x)$ y $latex g(x)$ generan una nueva función como $latex h(x)$ de tal forma que tenemos $latex h(x)=g(f(x))$.
Esto significa que la función $latex g$ es aplicada a la función $latex f(x)$. Entonces, básicamente, una función es aplicada al resultado de otra función.
Símbolo: Una composición de funciones también es denotada como $latex (g\circ f)(x)$, en donde, el círculo pequeño, $latex \circ$, es el símbolo de composición de funciones. No podemos reemplazar al círculo con un punto (·) ya que esto indica el producto de dos funciones.
Dominio: La composición $latex f(g(x))$ es leída como “f de g de x”. En esta composición, el dominio de la función f se vuelve $latex g(x)$ ya que el dominio es el conjunto de todos los valores de entrada de la función.
Para aplicar la composición $latex f\circ g$, realizamos los siguientes dos pasos:
Paso 1: Aplicamos la función g a la entrada x y obtenemos el resultado $latex g(x)$ como la salida.
Paso 2: Aplicamos la función f usando $latex g(x)$ como la entrada y obtenemos el resultado $latex f(g(x))$ como la salida.
→ Cursos Gratis: Explora Nuestros Cursos de Matemáticas
Ejercicios de composición de funciones resueltos
Los siguientes ejercicios de composición de funciones pueden ser usados para entender completamente el proceso usado para obtener una composición de funciones. Es recomendable intentar resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Encuentra la composición $latex f(g(x))$ si es que tenemos las funciones $latex f(x)=2x+3$ y $latex g(x)=x+1$.
Solución
Para encontrar la combinación $latex f(g(x))$, tenemos que usar las salidas de la función $latex g(x)$ en las entradas de $latex f(x)$.
Entonces, usamos a $latex x+1$ como las entradas de la función f y tenemos:
$latex f(g(x))=2(x+1)+3$
$latex f(g(x))=2x+2+3$
$latex f(g(x))=2x+5$
EJERCICIO 2
Encuentra la composición $latex f\circ g$ si es que tenemos las funciones $latex f(x)={{x}^2}+5$ y $latex g(x)=x+1$.
Solución
La composición $latex f\circ g$ también puede ser escrita como $latex f(g(x))$. Entonces, tenemos que tomar la salida de $latex g(x)$ y usarla como la entrada de $latex f(x)$.
Empezamos sustituyendo cada valor de x en la función f por la función g:
$latex f(g(x))={{(x+1)}^2}+5$
Ahora, podemos aplicar el exponente para expandir y simplificar a la función:
$latex f(g(x))={{x}^2}+2x+1+5$
$latex f(g(x))={{x}^2}+2x+6$
EJERCICIO 3
Tenemos a las funciones $latex f(x)=2{{x}^2}+3x-10$ y $latex g(x)=-x+2$. Encuentra la composición $latex f\circ g$.
Solución
Similar al ejercicio anterior, sabemos que la composición $latex f\circ g$ puede ser escrita como $latex f(g(x))$. Entonces, reemplazamos cada x en la función $latex f(x)$ con la función $latex g(x)$.
Luego, expandimos el paréntesis con exponente y simplificamos la función compuesta:
$$f\circ g=2{{(-x+2)}^2}+3(-x+2)-10$$
$latex =2({{x}^2}-2x+4)-3x+6-10$
$latex =2{{x}^2}-4x+8-3x+6-10$
$latex f\circ g=2{{x}^2}-7x+4$
EJERCICIO 4
Realiza la composición de funciones $latex g\circ f$ si es que tenemos las funciones $latex f(x)=6{{x}^2}+8x-10$ y $latex g(x)=\frac{1}{2}x+5$.
Solución
En este caso tenemos la composición $latex g\circ f$ que es igual que $latex g(f(x))$. Por lo tanto, usamos las salidas de $latex f(x)$ como las entradas de $latex g(x)$:
$latex g\circ f=\frac{1}{2}(6{{x}^2}+8x-10)+5$
$latex =3{{x}^2}+4x-5+5$
$latex g\circ f=3{{x}^2}+4x$
EJERCICIO 5
Tenemos las funciones $latex f(x)=2{{x}^2}+5$ y $latex g(x)=\sqrt{-2x+4}$. Encuentra la composición $latex f(g(x))$.
Solución
Tenemos que tomar a la función $latex g(x)$ y usarla como la entrada de $latex f(x)$. En este caso, la función $latex g(x)$ tiene una raíz cuadrada. Veamos lo que sucede al expandir y simplificar:
$latex f(g(x))=2{{(\sqrt{-2x+4})}^2}+5$
$latex =2(-2x+4)+5$
$latex =-4x+8+5$
$latex =-4x+13$
EJERCICIO 6
Calcula la composición $latex g\circ f$ si es que tenemos las funciones $latex f(x)=16\sqrt{x+2}$ y $latex g(x)=\sqrt{x}$.
Solución
Sabemos que esta composición es equivalente a tener $latex g(f(x))$. Entonces, usamos a las salidas de $latex f(x)$ como las entradas de $latex g(x)$.
Este caso es interesante, ya que tenemos a una raíz cuadrada que va dentro de otra raíz cuadrada:
$latex g\circ f=\sqrt{16\sqrt{x+2}}$
$latex =4\sqrt{\sqrt{x+2}}$
Podemos escribir a los radicales como expresiones exponenciales con exponentes fraccionarios y luego aplicar la regla de la potencia de una potencia para simplificar:
$latex 4\sqrt{\sqrt{x+2}}=4{{[{{(x+2)}^{\frac{1}{2}}}]}^{\frac{1}{2}}}$
$latex =4{{(x+2)}^{\frac{1}{4}}}$
Ahora, reescribimos a la expresión exponencial como la raíz cuarta:
$latex g\circ f=4\sqrt[4]{x+2}$
EJERCICIO 7
Si es que tenemos $latex f(x)=3{{x}^2}+2x-6$, realiza la composición de funciones $latex f\circ f$.
Solución
En los anteriores ejercicios solo hemos visto composiciones de dos funciones diferentes.
Sin embargo, también es posible tener composiciones de la misma función. Solo tenemos que reemplazar cada valor de x por la función misma:
$$f\circ f=3{{(3{{x}^2}+2x-6)}^2}+2(3{{x}^2}+2x-6)-6$$
$$=3(9{{x}^4}+12{{x}^3}-32{{x}^2}-24x+36)+6{{x}^2}+4x-12-6$$
$$=27{{x}^4}+36{{x}^3}-96{{x}^2}-72x+108+6{{x}^2}+4x-12-6$$
$$f\circ f=27{{x}^4}+36{{x}^3}-90{{x}^2}-68x+90$$
Únete a nuestros cursos interactivos o practica con nuestros generadores de problemas
Ejercicios de composición de funciones para resolver
Pon en práctica lo aprendido sobre composición de funciones resolviendo los siguientes ejercicios. Escoge una respuesta y verifícala para saber si obtuviste la respuesta correcta.
Mira los ejercicios resueltos de arriba en caso de necesitar ayuda.
→ Explora más ejercicios de práctica
Véase también
¿Interesado en aprender más sobre funciones algebraicas? Mira estas páginas:
