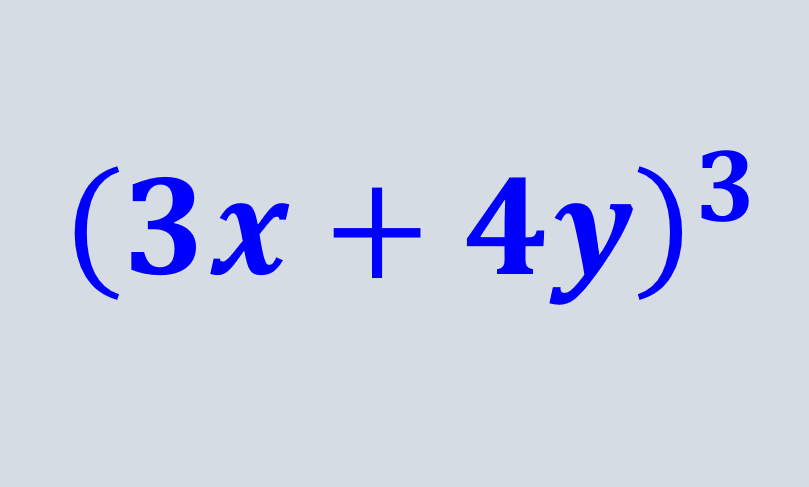Los ejercicios de binomios al cubo pueden ser resueltos usando dos métodos. El primer método consiste en multiplicar al binomio tres veces y expandir totalmente la expresión. El segundo método consiste en usar una fórmula estándar que puede simplificar el proceso de resolución.
A continuación, veremos un resumen de estos dos métodos para resolver binomios al cubo. Además, exploraremos varios ejercicios resueltos para dominar completamente este tema.
Resumen de binomios al cubo
Recordemos que un binomio al cubo es una expresión de la forma $latex {{(x+y)}^3}$. Esta expresión podría contener coeficientes u otras variables.
Para resolver binomios al cubo, podemos usar dos métodos principales:
Método 1: Podemos reescribir al binomio tres veces como una multiplicación de binomios y eliminamos al exponente. Por ejemplo, podemos reescribir a $latex {{(x+y)}^3}$, de la siguiente forma:
$latex (x+y)(x+y)(x+y)$
Luego, usamos la propiedad distributiva para multiplicar todos los términos y obtener una expresión simplificada.
Método 2: El método 1 podría resultar muy tedioso, ya que tenemos que multiplicar a cada término por cada término. Para facilitar la resolución de binomios al cubo, podemos usar fórmulas estándar para la suma de cubos y la resta de cubos.
Suma de cubos: La suma de un binomio al cubo es igual al primer término al cubo, más tres veces el cuadrado del primer término por el segundo término, más tres veces el primer término por el cuadrado del segundo término, más el cubo del segundo término:
| $latex {{(a+b)}^3}={{a}^3}+3{{a}^2}b+3a{{b}^2}+{{b}^3}$ |
Diferencia de cubos: La diferencia de un binomio al cubo es igual al primer término al cubo, menos tres veces el cuadrado del primer término por el segundo término, más tres veces el primer término por el cuadrado del segundo término, menos el cubo del segundo término:
| $latex {{(a+b)}^3}={{a}^3}-3{{a}^2}b+3a{{b}^2}-{{b}^3}$ |
Ejercicios de binomios al cubo resueltos
Los siguientes ejercicios de binomios al cubo pueden ser usados para aprender cómo aplicar los métodos de resolución mencionados arriba. Es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Resuelve el binomio $latex {{(x+1)}^3}$.
Solución
Método 1: Tenemos que reescribir al binomio como una multiplicación:
$latex {{(x+1)}^3}$
⇒ $latex (x+1)(x+1)(x+1)$
Empezamos multiplicando los primeros dos paréntesis y luego multiplicamos los paréntesis restantes:
$latex (x+1)(x+1)(x+1)$
$latex =({{x}^2}+2x+1)(x+1)$
$latex ={{x}^3}+3{{x}^2}+3x+1$
Método 2: Usando la fórmula para la suma de un binomio al cubo $latex {{(a+b)}^3}={{a}^3}+3{{a}^2}b+3a{{b}^2}+{{b}^3}$, tenemos:
⇒ $latex {{x}^3}+3{{x}^2}(1)+3x{{1}^2}+{{1}^3}$
$latex ={{x}^3}+3{{x}^2}+3x+1$
Vemos que obtuvimos la misma respuesta usando ambos métodos.
Sin embargo, el primer método suele ser más tedioso cuando tenemos binomios más complicados, por lo que solo usaremos el segundo método para resolver los próximos ejercicios.
EJERCICIO 2
Encuentra el resultado del binomio al cubo $latex {{(x+5)}^3}$.
Solución
Usando la fórmula para la suma de un binomio al cubo $latex {{(a+b)}^3}={{a}^3}+3{{a}^2}b+3a{{b}^2}+{{b}^3}$, tenemos:
⇒ $latex {{x}^3}+3{{x}^2}(5)+3x{{(5)}^2}+{{5}^3}$
$latex ={{x}^3}+15{{x}^2}+75x+125$
Vemos que con la fórmula estándar podemos encontrar más fácilmente la respuesta.
EJERCICIO 3
Resuelve el binomio al cubo $latex {{(2x-6)}^3}$.
Solución
En este caso, tenemos que usar la fórmula para la resta de un binomio al cubo $latex {{(a-b)}^3}={{a}^3}-3{{a}^2}b+3a{{b}^2}-{{b}^3}$. Entonces, tenemos:
⇒ $latex {{(2x)}^3}-3{{(2x)}^2}(6)+3(2x){{(6)}^2}-{{6}^3}$
$$=8{{x}^3}-3(4{{x}^2})(6)+3(2x)(36)-216$$
$latex =8{{x}^3}-72{{x}^2}+216x-216$
Fácilmente pudimos encontrar la respuesta al usar la fórmula.
EJERCICIO 4
Resuelve el binomio al cubo $latex {{(3x-2y)}^3}$.
Solución
Tenemos que usar la fórmula de la resta de un binomio al cubo $latex {{(a-b)}^3}={{a}^3}-3{{a}^2}b+3a{{b}^2}-{{b}^3}$. Entonces, tenemos:
⇒ $${{(3x)}^3}-3{{(3x)}^2}(2y)+3(3x){{(2y)}^2}-{{(2y)}^3}$$
$$=27{{x}^3}-3(9{{x}^2})(2y)+3(3x)(4{{y}^2})-8{{y}^3}$$
$latex =27{{x}^3}-54{{x}^2}y+36x{{y}^2}-8{{y}^3}$
EJERCICIO 5
Resuelve el binomio al cubo $latex {{(2{{x}^2}+4y)}^3}$.
Solución
Aquí, tenemos que usar la fórmula para la suma de un binomio al cubo $latex {{(a+b)}^3}={{a}^3}+3{{a}^2}b+3a{{b}^2}+{{b}^3}$. Entonces, tenemos:
⇒ $${{(2{{x}^2})}^3}+3{{(2{{x}^2})}^2}(4y)+3(2{{x}^2}){{(4y)}^2}+{{(4y)}^3}$$
$$ =8{{x}^6}+3(4{{x}^4})(4y)+3(2{{x}^2})(16{{y}^2})+64{{x}^3}$$
$$=8{{x}^6}+48{{x}^4}y+96{{x}^2}{{y}^2}+64{{x}^3}$$
Este binomio contenía una variable elevada al cuadrado, pero aplicamos la fórmula de la suma del binomio de la misma forma que en los anteriores ejercicios.
Simplemente usamos la regla de la potencia de una potencia, la cual nos indica que cuando elevamos a una expresión con una potencia a otra potencia, tenemos que multiplicar los exponentes.
EJERCICIO 6
Simplifica la siguiente expresión $latex {{(x+2y)}^3}+{{(x-2y)}^3}$.
Solución
Podemos usar las fórmulas de la suma de un binomio al cubo y la resta de un binomio al cubo separadamente para calcular cada binomio. Entonces, tenemos:
⇒ $${{(x)}^3}+3{{(x)}^2}(2y)+3(x){{(2y)}^2}+{{(2y)}^3}$$
$latex ={{x}^3}+3({{x}^2})(2y)+3(x)(4{{y}^2})+8{{y}^3}$
$latex ={{x}^3}+6{{x}^2}y+12x{{y}^2}+8{{y}^3}$
⇒ $${{(x)}^3}-3{{(x)}^2}(2y)+3(x){{(2y)}^2}-{{(2y)}^3}$$
$latex ={{x}^3}-3({{x}^2})(2y)+3(x)(4{{y}^2})-8{{y}^3}$
$latex ={{x}^3}-6{{x}^2}y+12x{{y}^2}-8{{y}^3}$
Ahora, podemos sumar ambas expresiones obtenidas y simplificar términos semejantes:
$latex ={{x}^3}+6{{x}^2}y+12x{{y}^2}+8{{y}^3}$ $latex +{{x}^3}-6{{x}^2}y+12x{{y}^2}-8{{y}^3}$
$latex =2{{x}^3}+24x{{y}^2}$
Ejercicios de binomios al cubo para resolver
Usa las fórmulas de la suma de un binomio al cubo y la resta de un binomio al cubo revisadas arriba para resolver los siguientes ejercicios. Si tienes problemas con estos ejercicios, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre factorización de expresiones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
