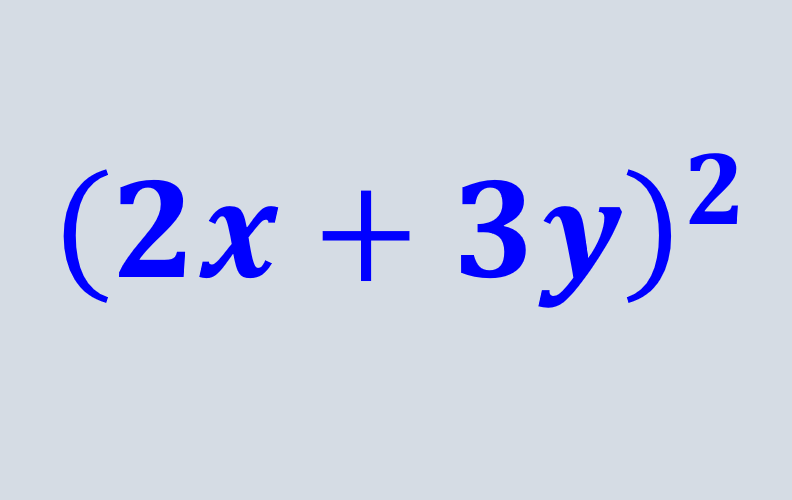Los binomios al cuadrado pueden ser expandidos usando dos métodos principales. Podemos escribir al binomio dos veces y realizar la multiplicación o podemos usar una fórmula estándar y reemplazar los valores.
A continuación, veremos un resumen de estos dos métodos para resolver binomios al cuadrado. Además, veremos varios ejercicios resueltos para entender cómo aplicar estos métodos y dominar completamente la expansión de binomios al cuadrado.
Resumen de binomios al cuadrado
Un binomio al cuadrado es una expresión que tiene la forma general $latex {{(ax+b)}^2}$. Esta expresión podría contener a otras variables aparte de la x. Por ejemplo, la expresión $latex {{(5x+4y)}^2}$ es un binomio al cuadrado.
Existen dos métodos principales que pueden ser usados para resolver binomios al cuadrado:
Primer método
El primer método consiste en escribir al binomio dos veces y eliminar el exponente. Luego, multiplicar los binomios usando la propiedad distributiva o cualquier otro método. Finalmente, combinamos términos semejantes para simplificar la expresión resultante.
Segundo método
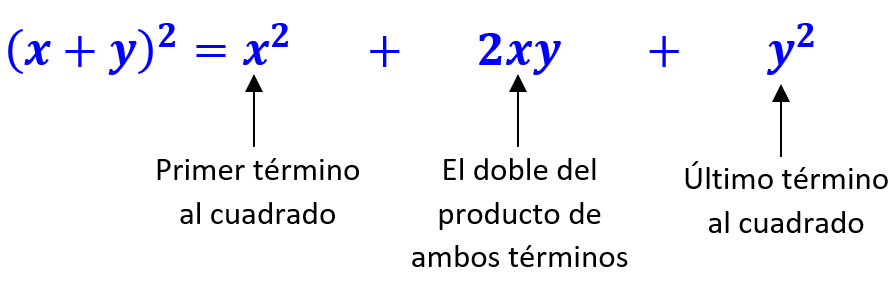
El segundo método consiste en usar una fórmula estándar que nos indica que el cuadrado de un binomio es igual a la suma del cuadrado del primer término, el doble del producto de ambos términos y el cuadrado del último término.
Ejercicios de binomios al cuadrado resueltos
Los siguientes ejercicios usan ambos métodos mencionados arriba para expandir los binomios al cuadrado. Es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Resuelve este binomio $latex {{(2x+4)}^2}$.
Solución
Método 1: Reescribimos al binomio de la siguiente manera:
$latex{{(2x+4)}^2}$
⇒ $latex (2x+4)(2x+4)$
Ahora, podemos multiplicar usando la propiedad distributiva:
⇒ $latex 2x(2x+4)+4(2x+4)$
$latex =4{{x}^2}+8x+8x+16$
Combinamos términos semejantes para simplificar:
$latex =4{{x}^2}+16x+16$
Método 2: Usando la fórmula estándar, tenemos que encontrar el cuadrado del primer término, el doble del producto de ambos términos y el cuadrado del último término:
⇒ $latex {{(2x)}^2}+2(2x)(4)+{{4}^2}$
Simplificando, tenemos:
⇒ $latex 4{{x}^2}+16x+16$
Obtuvimos la misma respuesta con ambos métodos, por lo que ambos métodos son válidos.
EJERCICIO 2
Resuelve este binomio $latex {{(3x-5)}^2}$.
Solución
Método 1: Eliminamos al exponente y escribimos al binomio dos veces:
$latex{{(3x-5)}^2}$
⇒ $latex (3x-5)(3x-5)$
Con la propiedad distributiva, podemos multiplicar y expandir:
⇒ $latex 3x(3x-5)-5(3x-5)$
$latex =9{{x}^2}-15x-15x+25$
Simplificamos al combinar términos semejantes:
$latex =9{{x}^2}-30x+25$
Método 2: Encontramos el cuadrado del primer término, el doble del producto de ambos términos y el cuadrado del último término:
⇒ $latex {{(3x)}^2}+2(3x)(-5)+{{(-5)}^2}$
Simplificando, tenemos:
⇒ $latex 9{{x}^2}-30x+25$
EJERCICIO 3
Expande al binomio al cuadrado: $latex {{(-4x+10)}^2}$.
Solución
Método 1: Escribimos al binomio dos veces y eliminamos el exponente:
$latex{{(-4x+10)}^2}$
⇒ $latex (-4x+10)(-4x+10)$
Multiplicamos usando la propiedad distributiva:
⇒ $latex -4x(-4x+10)+10(-4x+10)$
$latex =16{{x}^2}-40x-40x+100$
Combinamos términos semejantes para simplificar:
$latex =16{{x}^2}-80x+100$
Método 2: Para usar este método encontramos el cuadrado del primer término, el doble del producto de ambos términos y el cuadrado del último término:
⇒ $latex {{(-4x)}^2}+2(-4x)(10)+{{10}^2}$
Simplificando, tenemos:
⇒ $latex 16{{x}^2}-80x+100$
EJERCICIO 4
Resuelve este binomio al cuadrado: $latex {{(5x+2y)}^2}$.
Solución
Método 1: Eliminamos el exponente y reescribimos al binomio de la siguiente manera:
$latex{{(5x+2y)}^2}$
⇒ $latex (5x+2y)(5x+2y)$
Expandimos y multiplicamos para eliminar los paréntesis:
⇒ $latex 5x(5x+2y)+2y(5x+2y)$
$latex =25{{x}^2}+10xy+10xy+4{{y}^2}$
Simplificando, tenemos:
$latex =25{{x}^2}+20xy+4{{y}^2}$
Método 2: Para usar la fórmula estándar, encontramos el cuadrado del primer término, el doble del producto de ambos términos y el cuadrado del último término:
⇒ $latex {{(5x)}^2}+2(5x)(2y)+{{(2y)}^2}$
Simplificando, tenemos:
⇒ $latex 25{{x}^2}+20xy+4{{y}^2}$
EJERCICIO 5
Resuelve este binomio al cuadrado: $latex {{(3{{x}^2}+4y)}^2}$.
Solución
Método 1: Reescribimos al binomio de la siguiente manera:
$latex{{(3{{x}^2}+4y)}^2}$
⇒ $latex (3{{x}^2}+4y)(3{{x}^2}+4y)$
Ahora, multiplicamos usando la propiedad distributiva:
⇒ $latex 3{{x}^2}(3{{x}^2}+4y)+4y(3{{x}^2}+4y)$
$latex =9{{x}^4}+12{{x}^2}y+12{{x}^2}y+16{{y}^2}$
Simplificando, tenemos:
$latex =9{{x}^4}+24{{x}^2}y+16{{y}^2}$
Método 2: Encontramos el cuadrado del primer término, el doble del producto de ambos términos y el cuadrado del último término para usar la fórmula estándar:
⇒ $latex {{(3{{x}^2})}^2}+2(3{{x}^2})(4y)+{{(4y)}^2}$
Simplificando, tenemos:
⇒ $latex 9{{x}^4}+24{{x}^2}y+16{{y}^2}$
EJERCICIO 6
Resuelve el binomio $latex {{(5{{x}^2}-2{{y}^2})}^2}$.
Solución
Método 1: Eliminamos el exponente y escribimos al binomio dos veces:
$latex{{(5{{x}^2}-2{{y}^2})}^2}$
⇒ $latex (5{{x}^2}-2{{y}^2})(5{{x}^2}-2{{y}^2})$
Usamos la propiedad distributiva para multiplicar:
⇒ $latex 5{{x}^2}(5{{x}^2}-2{{y}^2})-2{{y}^2}(5{{x}^2}-2{{y}^2})$
$latex =25{{x}^4}-10{{x}^2}{{y}^2}-10{{x}^2}{{y}^2}+4{{y}^4}$
Simplificando, tenemos:
$latex =25{{x}^4}-20{{x}^2}{{y}^2}-4{{y}^4}$
Método 2: Encontramos el cuadrado del primer término, el doble del producto de ambos términos y el cuadrado del último término para usar la fórmula estándar:
⇒ $latex {{(5{{x}^2})}^2}+2(5{{x}^2})(-2{{y}^2})+{{(-2{{y}^2})}^2}$
Simplificando, tenemos:
⇒ $latex 25{{x}^4}-20{{x}^2}{{y}^2}+4{{y}^4}$
Ejercicios de binomios al cuadrado para resolver
Practica lo aprendido con los siguientes ejercicios. Expande los binomios al cuadrado y escoge una respuesta. Si es que necesitas ayuda, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre factorización de expresiones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
