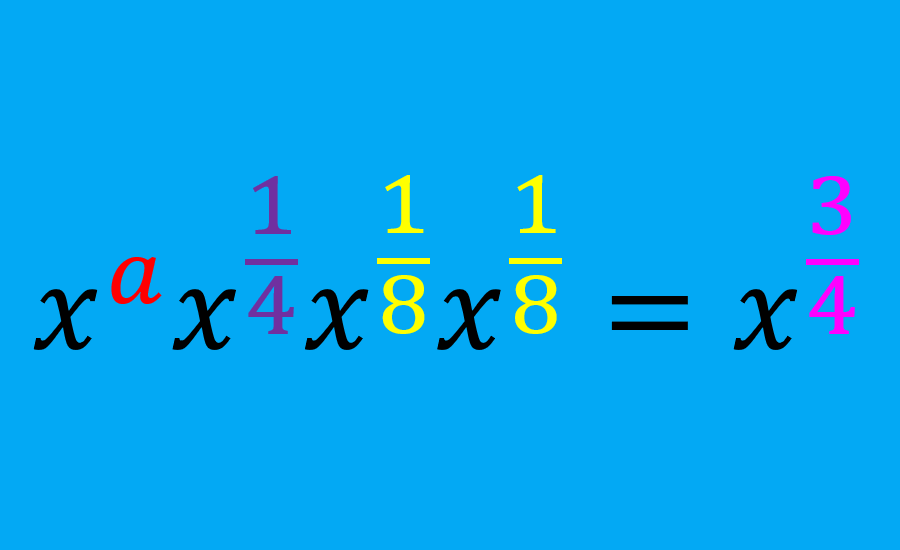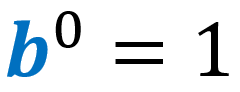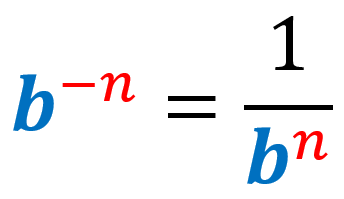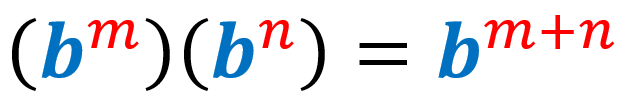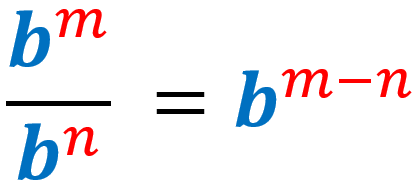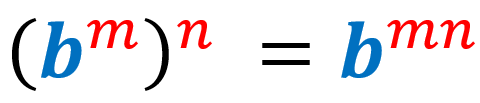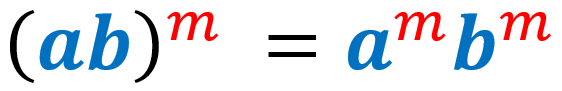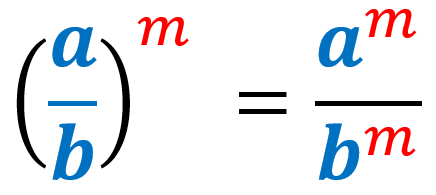Los exponentes son maneras más simples de escribir multiplicación repetida. Sin embargo, incluso con exponentes, las expresiones algebraicas pueden volverse extensas y tediosas. Las leyes de los exponentes nos permiten simplificar expresiones algebraicas que contienen operaciones con exponentes. Conocimiento sobre estas leyes de los exponentes hará que nuestro estudio del álgebra sea más productivo.
A continuación, miraremos un resumen de las siete leyes de los exponentes junto con ejercicios resueltos para entender el razonamiento usado a la hora de simplificar expresiones algebraicas.
Resumen de leyes de exponentes
Las leyes de los exponentes nos indican cómo resolver ecuaciones o simplificar expresiones que contienen exponentes. Los exponentes, también conocidos como potencias, son valores que nos indican cuántas veces debemos multiplicar a un número por sí mismo.
Por ejemplo, si tenemos $latex {{5}^3}$, esto significa que multiplicamos al 5 por sí mismo 3 tres veces:
$latex {{5}^3}=5\times 5\times 5=125$
El número que está siendo elevado a un exponente se llama la base. En este caso, la base es 5. El número pequeño es el exponente. En este caso, el exponente es 3.
Existen diferentes tipos de expresiones exponenciales, las cuales parecieran ser tediosas a primera vista. Sin embargo, existen ciertas estrategias que pueden ser usadas para hacer que las leyes de los exponentes sean fáciles de seguir.
Hay siete leyes de los exponentes que nos ayudan a simplificar expresiones exponenciales. Cada ley muestra cómo resolver diferentes tipos de operaciones matemáticas como sumar, restar, multiplicar y dividir exponentes.
En las siguientes leyes, las letras a y b representan a números reales diferentes de cero y m y n representan a números enteros:
1) Ley del cero de exponentes:
2) Ley de exponentes negativos:
3) Ley del producto de exponentes:
4) Ley del cociente de exponentes:
5) Ley de Potencia de una potencia de exponentes:
6) Ley de potencia de un producto de exponentes:
7) Ley de potencia de un cociente de exponentes:
Ejercicios con leyes de exponentes resueltos
Los siguientes ejercicios ponen en práctica las leyes de los exponentes para simplificar las expresiones algebraicas. Intenta resolver los ejercicios tú mismo. Sin embargo, cada ejercicio tiene su solución detallada para que puedas seguir el razonamiento usado en cada problema.
EJERCICIO 1
Encuentra el resultado de $latex 8^{-2}$.
Solución
Para resolver el exponente negativo, aplicamos la ley de exponentes negativos, la cual nos indica que podemos cambiar un exponente de negativo a positivo al tomar el recíproco de su base:
$latex 8^{-2}=\frac{1}{8^2}$
Ahora, elevamos al 8 al cuadrado para simplificar:
$latex \frac{1}{{{8}^2}}=\frac{1}{64}$
EJERCICIO 2
Simplifica la expresión $latex {{({{2}^3})}^{-2}}$.
Solución
Aquí, aplicamos la ley de la potencia de una potencia, la cual nos indica que tenemos que multiplicar los exponentes:
$latex {{({{2}^3})}^{-2}}={{2}^{-6}}$
Nuevamente, aplicamos la ley de exponentes negativos para cambiar el exponente 6 negativo a 6 positivo:
$latex {{2}^{-6}}=\frac{1}{{{2}^6}}$
Simplificando, tenemos:
$latex \frac{1}{{{2}^6}}=\frac{1}{64}$
EJERCICIO 3
Encuentra el resultado de $latex \frac{{{5}^6}}{{{5}^4}}$.
Solución
Aplicamos la ley del cociente para simplificar la división de potencias. Entonces, tenemos la base 4 y restamos el exponente del denominador al exponente del numerador:
$latex \frac{{{5}^6}}{{{5}^4}}={{5}^{6-4}}$
$latex ={{5}^2}$
Aplicando el exponente tenemos:
$latex {{5}^2}=25$
EJERCICIO 4
Encuentra el resultado de $latex \frac{{{5}^4}\times {{3}^4}}{{{15}^2}}$.
Solución
Tenemos bases diferentes en el numerador, por lo que no podemos simplificar. Sin embargo, observamos que la base puede ser reescrita ya que 15 es igual a 5×3:
$latex \frac{{{5}^4}\times {{3}^4}}{{{15}^2}}=\frac{{{5}^4}\times {{3}^4}}{{{(5\times 3)}^2}}$
$latex =\frac{{{5}^4}\times {{3}^4}}{{{5}^2}\times {{3}^2}}$
Ahora, aplicamos la ley del cociente tanto a la potencia con base 5 como a la potencia con base 3:
$latex \frac{{{5}^4}\times {{3}^4}}{{{5}^2}\times {{3}^2}}={{5}^{4-2}}\times {{3}^{4-2}}$
$latex ={{5}^2}\times {{3}^2}$
$latex =25\times 9$
$latex =225$
EJERCICIO 5
Simplifica la expresión $latex {{\left(\frac{2}{{{3}^2}} \right)}^{-3}} \times \left(\frac{{{2}^3}}{{{3}^2}} \right)$.
Solución
Empezamos cambiando el exponente negativo a positivo al darle la vuelta a la fracción:
$latex {{\left(\frac{2}{{{3}^2}} \right)}^{-3}} \times \left(\frac{{{2}^3}}{{{3}^2}} \right)={{\left(\frac{{{3}^2}}{2} \right)}^3} \times \left(\frac{{{2}^3}}{{{3}^2}} \right)$
Ahora, aplicamos la ley de la potencia de una potencia:
$latex {{\left(\frac{{{3}^2}}{2} \right)}^3} \times \left(\frac{{{2}^3}}{{{3}^2}} \right)=\frac{{{3}^6}}{{{2}^3}} \times \frac{{{2}^3}}{{{3}^2}} $
Podemos reescribir la expresión para aplicar la ley del cociente:
$latex \frac{{{3}^6}}{{{2}^3}} \times \frac{{{2}^3}}{{{3}^2}}=\frac{{{3}^6}}{{{3}^2}} \times \frac{{{2}^3}}{{{2}^3}}$
$latex ={{3}^{6-2}}\times{{2}^{3-3}}$
Simplificando y aplicando la ley del cero de exponentes, tenemos:
$latex {{3}^{6-2}}\times{{2}^{3-3}}={{3}^4}\times {{2}^0}$
$latex =81\times 1$
$latex =81$
EJERCICIO 6
Simplifica la expresión algebraica $$\frac{{{a}^{-3}}{{b}^{2}}}{{{b}^2}{{a}^2}}$$
Solución
En este ejercicio, tenemos a las variables a y b, pero aplicamos las leyes de los exponentes de la misma forma. Entonces, empezamos con la ley de exponentes negativos:
$latex \frac{{{a}^{-3}}{{b}^2}}{{{b}^2}{{a}^2}}=\frac{{{b}^2}}{{{b}^2}{{a}^2}{{a}^3}}$
Ahora, aplicamos la ley del cociente a la variable a y la ley del producto a la variable b:
$latex \frac{{{b}^2}}{{{b}^2}{{a}^2}{{a}^3}}=\frac{{{b}^{2-2}}}{{{a}^{2+3}}}$
$latex =\frac{1}{{{a}^5}}$
EJERCICIO 7
Simplifica la expresión $latex {{(10{{x}^4})}^{-2}}{{y}^{-1}}$.
Solución
Empezamos aplicando la ley de exponentes negativos. Entonces, tomamos el recíproco de las bases y cambiamos los exponentes a positivos:
$latex {{(10{{x}^4})}^{-2}}{{y}^{-1}}=\frac{1}{{{(10{{x}^4})}^2}{{y}^1}}$
Ahora, aplicamos la ley de la potencia de una potencia:
$latex \frac{1}{{{(10{{x}^4})}^2}{{y}^1}}=\frac{1}{{{10}^2}{{x}^8}{{y}^1}}$
$latex =\frac{1}{100{{x}^8}y}$
EJERCICIO 8
Simplifica la expresión $latex {{({{x}^{-3}}z)}^2}\times {{({{x}^{2}}{{z}^3})}^{-3}}$.
Solución
Empezamos aplicando la ley de exponentes negativos a la parte derecha:
$latex {{({{x}^{-3}}z)}^2}\times {{({{x}^{2}}{{z}^3})}^{-3}}=\frac{{{({{x}^{-3}}z)}^2}}{{{({{x}^{2}}{{z}^3})}^3}}$
Eliminamos los paréntesis al aplicar la ley de la potencia de una potencia:
$latex \frac{{{({{x}^{-3}}z)}^2}}{{{({{x}^{2}}{{z}^3})}^3}}=\frac{{{x}^{-6}}{{z}^2}}{{{x}^6}{{z}^9}}$
Aplicamos la ley de exponentes negativos otra vez:
$latex \frac{{{x}^{-6}}{{z}^2}}{{{x}^6}{{z}^9}}=\frac{{{z}^2}}{{{x}^6}{{x}^6}{{z}^9}}$
Ahora, aplicamos la ley del cociente a z y la ley del producto a x:
$latex \frac{{{z}^2}}{{{x}^6}{{x}^6}{{z}^9}}=\frac{1}{{{x}^{6+6}}{{z}^{9-2}}}$
$latex =\frac{1}{{{x}^{12}}{{z}^7}}$
Ejercicios con leyes de exponentes para resolver
Pon a prueba tu conocimiento sobre las leyes de los exponentes con los siguientes ejercicios. Simplifica o resuelve las expresiones y selecciona la respuesta correcta. Mira los ejercicios resueltos de arriba si necesitas ayuda.
Véase también
¿Interesado en aprender más sobre potencias? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
