Los ejercicios de exponentes fraccionarios pueden ser resueltos usando la regla de exponentes fraccionarios. Esta regla indica la relación entre potencias y radicales. El denominador de un exponente fraccionario es escrito como un radical de la expresión y el numerador es escrito como el exponente.
A continuación, veremos un breve resumen de exponentes fraccionarios en expresiones algebraicas. También miraremos varios ejercicios de exponentes fraccionarios resueltos para aprender cómo resolver este tipo de problemas.
Resumen de exponentes fraccionarios
Un exponente fraccionario es una técnica para expresar potencias y raíces juntas. La forma general de un exponente fraccionario es:
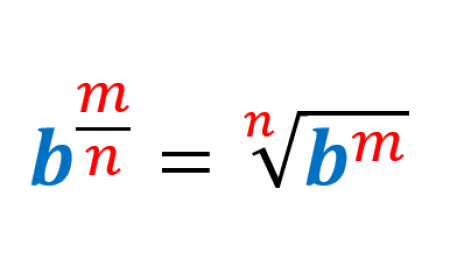
Podemos definir los siguientes términos:
- Radicando: El radicando es la expresión debajo del signo √. En la expresión de arriba, el radicando es $latex {{b}^m}$.
- Índice: El índice o también conocido como orden del radical, es el número que indica cuál raíz está siendo aplicada. En la expresión de arriba, el índice es n.
- Base: La base es el número al cual se aplica la raíz o la potencia. En este caso, la base es b.
- Potencia: La potencia indica multiplicación repetida de la base por sí misma. En la expresión de arriba, la potencia es m.
Cambio de la forma radical a exponente fraccionario
Para cambiar de la forma radical a exponente fraccionario, tenemos que usar la regla de exponentes fraccionarios inversamente.
Podemos formar un exponente fraccionario en donde el numerador es el exponente al que la base está elevada y el denominador es el índice del radical. Es decir, usamos la siguiente relación:
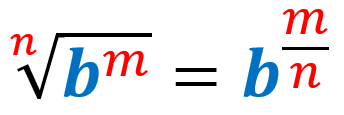
Ejercicios de exponentes fraccionarios resueltos
EJERCICIO 1
Simplifica la expresión $latex {{3}^{\frac{3}{2}}}$.
Solución
La regla de exponentes fraccionarios nos dice que $latex {{b}^{\frac{m}{n}}}=\sqrt[n]{{{b}^m}}$. Entonces, escribimos al 3 elevado a la potencia 3 y luego, sacamos la raíz cuadrada de esto:
$latex 3^{\frac{3}{2}}=\sqrt[2]{3^3}$
Ahora, simplificamos la expresión al aplicar el exponente del 3:
$latex \sqrt[2]{3^3}=\sqrt[2]{27}$
Podemos simplificar esto de la siguiente forma:
$latex \sqrt[2]{27}=\sqrt[2]{9 \times 3}$
$latex =3\sqrt{3}$
EJERCICIO 2
Simplifica la expresión $latex {{4}^{\frac{2}{3}}}$.
Solución
Ahora, tenemos que escribir al 4 elevado a la potencia de 2 y tenemos que sacar la raíz cúbica de esa expresión:
$latex 4^{\frac{2}{3}}=\sqrt[3]{4^2}$
Simplificamos al aplicar el exponente:
$latex \sqrt[3]{4^2}=\sqrt[3]{16}$
Podemos simplificar al reescribir al 16 como 8×2:
$latex \sqrt[3]{16}=\sqrt[3]{8\times 2}$
La raíz cúbica de 8 es 2, por lo que tenemos:
$latex \sqrt[3]{8\times 2}=2\sqrt[3]{2}$
EJERCICIO 3
Simplifica la expresión $latex {{-2}^{\frac{4}{3}}}{{x}^{\frac{2}{3}}}$.
Solución
Aquí tenemos un número y una variable. Elevamos al -2 a la cuarta potencia y sacamos su raíz cúbica y elevamos la x al cuadrado y sacamos su raíz cúbica:
$latex -2^{\frac{4}{3}}x^{\frac{2}{3}}=\sqrt[3]{(-2)^4}\sqrt[3]{x^2}$
Podemos aplicar el exponente al -2 para simplificar:
$latex \sqrt[3]{(-2)^4}\sqrt[3]{x^2}=\sqrt[3]{16}\sqrt[3]{x^2}$
Similar al problema anterior, Podemos simplificar al reescribir al 16 como 8×2:
$latex \sqrt[3]{16}=\sqrt[3]{8\times 2}$
$latex =2\sqrt[3]{2}$
Entonces, tenemos:
$latex \sqrt[3]{16}\sqrt[3]{x^2}=2\sqrt[3]{2}\sqrt[3]{x^2}$
Ahora, podemos combinar las raíces cúbicas para simplificar:
$latex 2\sqrt[3]{2}\sqrt[3]{x^2}=2\sqrt[3]{2x^2}$
EJERCICIO 4
Simplifica la expresión $latex {{6}^{\frac{3}{2}}}{{x}^{\frac{5}{2}}}$.
Solución
Escribimos al 6 elevado al cubo y sacamos su raíz cuadrada. Escribimos a la x elevada a la quinta y sacamos su raíz cuadrada:
$latex 6^{\frac{3}{2}}x^{\frac{5}{2}}=\sqrt{6^3}\sqrt{x^5}$
Simplificamos el 6 elevado al cubo:
$latex \sqrt{6^3}\sqrt{x^5}=\sqrt{216}\sqrt{x^5}$
Es posible simplificar al escribir al 216 como 36×6:
$latex \sqrt{216}=\sqrt{36\times 6}$
$latex =6\sqrt{6}$
Entonces, tenemos:
$latex \sqrt{216}\sqrt{x^5}=6\sqrt{6}\sqrt{x^5}$
Combinando las raíces cuadradas, tenemos:
$latex 6\sqrt{6}\sqrt{x^5}=6\sqrt{6x^5}$
EJERCICIO 5
Simplifica la expresión $latex {{4}^{-\frac{3}{2}}}{{x}^{\frac{1}{2}}}$.
Solución
En este caso, tenemos un exponente negativo. Recordemos que un exponente negativo puede ser transformado a positivo al tomar el recíproco de la base. Entonces, tenemos:
$latex {{4}^{-\frac{3}{2}}}{{x}^{\frac{1}{2}}}=\frac{{{x}^{\frac{1}{2}}}}{{{4}^{\frac{3}{2}}}}$
Ahora, elevamos al 4 al cubo y sacamos su raíz cuadrada y sacamos la raíz cuadrada de la x:
$latex \frac{{{x}^{\frac{1}{2}}}}{{{4}^{\frac{3}{2}}}}=\frac{\sqrt{x}}{\sqrt{{{4}^3}}}$
Podemos aplicar el exponente al 4 para simplificar:
$latex \frac{\sqrt{x}}{\sqrt{{{4}^3}}}=\frac{\sqrt{x}}{\sqrt{64}}$
Ahora, podemos sacar la raíz cuadrada de 64:
$latex \frac{\sqrt{x}}{\sqrt{64}}=\frac{\sqrt{x}}{8}$
EJERCICIO 6
Simplifica la expresión $latex {{12}^{-\frac{2}{3}}}{{x}^{\frac{3}{5}}}$.
Solución
Empezamos transformado el exponente a positivo al tomar el recíproco de la base. Entonces, tenemos:
$latex {{12}^{-\frac{2}{3}}}{{x}^{\frac{3}{5}}}=\frac{{{x}^{\frac{3}{5}}}}{{{12}^{\frac{2}{3}}}}$
Ahora, elevamos al 12 al cuadrado y sacamos su raíz cúbica. Elevamos a la x al cubo y sacamos su raíz quinta:
$latex \frac{{{x}^{\frac{3}{5}}}}{{{12}^{\frac{2}{3}}}}=\frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{{{12}^2}}}$
Aplicamos el exponente al 12:
$latex \frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{{{12}^2}}}=\frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{144}}$
Podemos escribir al 144 como 8×18 y samos la raíz cúbica del 8:
$latex \frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{144}}=\frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{8\times 18}}$
$latex =\frac{\sqrt[5]{{{x}^3}}}{2\sqrt[3]{18}}$
EJERCICIO 7
Simplifica la expresión $latex {{x}^{{\frac{1}{2}}}}{{y}^{{\frac{2}{3}}}}$.
Solución
Simplemente, aplicamos la regla de exponentes fraccionarios para formar radicales:
$latex {{x}^{{\frac{1}{2}}}}{{y}^{{\frac{2}{3}}}}=\sqrt{x}~\sqrt[3]{{{{y}^{2}}}}$
EJERCICIO 8
Simplifica la expresión $latex {{81}^{{\frac{1}{4}}}}{{x}^{{\frac{1}{2}}}}$
Solución
Nuevamente, sólo tenemos que aplicar la regla de exponentes fraccionarios para formar radicales y luego simplificamos:
$latex {{81}^{{\frac{1}{4}}}}{{x}^{{\frac{3}{2}}}}=\sqrt[4]{{81}}~\sqrt{{{{x}^{3}}}}$
$latex =3~\sqrt{{{{x}^{3}}}}$
EJERCICIO 9
Simplifica la expresión $latex {{4}^{{-\frac{1}{2}}}}{{x}^{{-\frac{1}{2}}}}$.
Solución
Aquí tenemos exponentes negativos, por lo que empezamos transformando los exponentes negativos a positivos al usar la regla de exponentes negativos:
$latex {{4}^{{-\frac{1}{2}}}}{{x}^{{-\frac{1}{2}}}}=\frac{1}{{{{4}^{{\frac{1}{2}}}}{{x}^{{\frac{1}{2}}}}}}$
Ahora, usamos la regla de exponentes fraccionarios y simplificamos:
$latex =\frac{1}{{\sqrt{4}~\sqrt{x}}}$
$latex =\frac{1}{{2~\sqrt{x}}}$
EJERCICIO 10
Simplifica la expresión $$\frac{{{{{16}}^{{-\frac{1}{2}}}}~{{y}^{{-\frac{1}{3}}}}}}{{{{x}^{{-\frac{1}{2}}}}~}}$$
Solución
Tenemos exponentes negativos, por lo que empezamos con la regla de exponentes negativos:
$$\frac{{{{{16}}^{{-\frac{1}{2}}}}~{{y}^{{-\frac{1}{3}}}}}}{{{{x}^{{-\frac{1}{2}}}}~}}=\frac{{{{x}^{{\frac{1}{2}}}}~}}{{{{{16}}^{{\frac{1}{2}}}}~{{y}^{{\frac{1}{3}}}}~}}$$
Ahora, usamos la regla de exponentes fraccionarios y simplificamos:
$latex =\frac{{\sqrt{x}}}{{\sqrt{{16}}~\sqrt[3]{y}}}$
$latex =\frac{{\sqrt{x}}}{{4~\sqrt[3]{y}}}$
Ejercicios de exponentes fraccionarios para resolver
Véase también
¿Interesado en aprender más sobre exponentes en expresiones algebraicas? Mira estas páginas:


