La ecuación de la recta tangente a una curva es encontrada usando la forma y=mx+b, en donde m es la pendiente de la recta y b es el intercepto en y. A su vez, encontramos la pendiente de la recta tangente usando la derivada de la función y evaluándola en el punto dado.
A continuación, veremos 10 ejercicios en los que encontraremos la ecuación de la recta tangente a una curva. Además, exploraremos 5 problemas de práctica.
CÁLCULO
Relevante para…
Resolver algunos ejercicios de la recta tangente a una curva.
CÁLCULO

Relevante para…
Resolver algunos ejercicios de la recta tangente a una curva.
Cómo encontrar la ecuación de la recta tangente a una curva
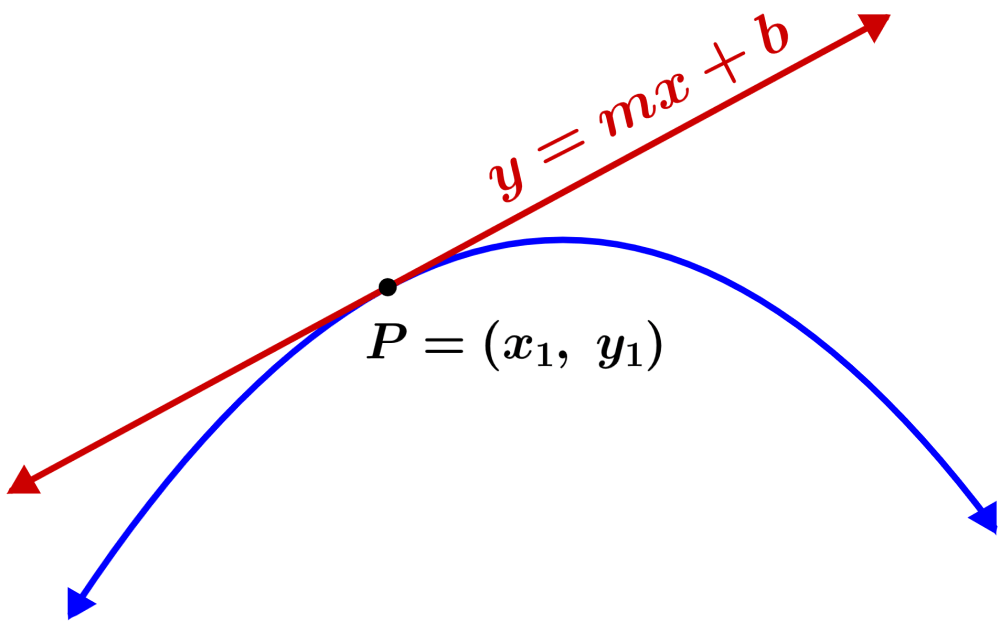
La ecuación de la recta tangente a una curva puede ser encontrada usando la forma $latex y=mx+b$, en donde m es la pendiente de la recta y b es el intercepto en y.

Entonces, si es que queremos encontrar la ecuación de la recta tangente a una curva en el punto $latex (x_{1},~y_{1})$, podemos seguir los siguientes pasos:
1. Encontrar la derivada de la función que representa a la curva.
2. Usar la derivada de la función para encontrar la pendiente de la recta tangente en el punto $latex (x_{1},~y_{1})$.
Para esto, usamos la coordenada en x del punto en la derivada de la función. Es decir, tenemos $latex m=f'(x_{1})$.
3. Usar la ecuación $latex y=mx+b$ para encontrar el valor de b.
Usar el valor de la pendiente encontrada en el paso 2 y sustituir las coordenadas en x y en y del punto dado para encontrar el valor de b. Es decir, tenemos $latex y_{1}=mx_{1}=b$.
4. Sustituir los valores de m y b en la ecuación $latex y=mx+b$.
Mira los siguientes ejemplos para conocer cómo aplicar estos pasos para encontrar la ecuación de la recta tangente a una función.
10 Ejercicios resueltos de la recta tangente a una curva
EJERCICIO 1
¿Cuál es la ecuación de la recta tangente a la curva $latex f(x)=x^2$ en el punto P=(1, 3)?
Solución
Para encontrar la ecuación de la tangente, podemos usar la forma $latex y=mx+b$, en donde m es la pendiente y b es el intercepto en y.
La pendiente de la recta tangente es encontrada al evaluar a la derivada de la función en el punto dado. Es decir, la pendiente es igual a $latex f'(1)$. Entonces, tenemos:
$latex f(x)=x^2$
$latex f'(x)=2x$
$latex m=f'(1)=2(1)$
$latex m=2$
Hasta ahora, tenemos la ecuación $latex y=2x+b$. Encontramos el valor de b usando el punto (1, 3) en la ecuación:
$latex y=2x+b$
$latex 3=2(1)+b$
$latex b=1$
La ecuación de la recta tangente en el punto (1, 3) es $latex y=2x+1$.
EJERCICIO 2
Encuentra la ecuación de la recta tangente a la función $latex f(x)=x^3-10x$ en el punto (2, 1).
Solución
Necesitamos la derivada de la función para encontrar la pendiente de la recta tangente. Entonces, tenemos:
$latex f(x)=x^3-10x$
$latex f'(x)=3x^2-10$
Para encontrar la pendiente de la recta tangente en el punto (2, 1), evaluamos $latex f'(2)$:
$latex m=f'(2)=3(2)^2-10$
$latex m=2$
Formamos la ecuación $latex y=2x+b$. Ahora, encontramos el valor de b, usando el punto (2, 1) en la ecuación:
$latex y=2x+b$
$latex 1=2(1)+b$
$latex b=-1$
La ecuación de la recta tangente en el punto (2, 1) es $latex y=2x-1$.
EJERCICIO 3
Si es que tenemos la función $latex f(x)=2x^3-7x^2$, encuentra la ecuación de su tangente en el punto (2, 3).
Solución
La derivada de la función nos permite encontrar la pendiente de la recta tangente. Entonces, la derivada es:
$latex f(x)=2x^3-7x^2$
$latex f'(x)=6x^2-14x$
La pendiente de la recta tangente en el punto (2, 3) es igual a $latex f'(2)$. Entonces, tenemos:
$latex m=f'(2)=6(2)^2-14(2)$
$latex m=24-28$
$latex m=-4$
Usando la pendiente encontrada, tenemos la ecuación $latex y=-4x+b$. Ahora, encontramos el valor de b, usando el punto (2, 3) en la ecuación:
$latex y=-4x+b$
$latex 3=-4(2)+b$
$latex b=11$
La ecuación de la recta tangente en el punto (2, 3) es $latex y=-4x+11$.
EJERCICIO 4
Tenemos la función $latex f(x)=x^3+\frac{8}{x}$. ¿Cuál es la recta tangente en el punto (2, 4)?
Solución
Empezamos encontrando la derivada de la función:
$latex f(x)=x^3+8x^{-1}$
$latex f'(x)=3x^2-8x^{-2}$
$latex f'(x)=3x^2-\frac{8}{x^2}$
La pendiente de la tangente en el punto (2, 4) es encontrada al evaluar $latex f'(2)$. Entonces, tenemos:
$latex m=f'(2)=3(2)^2-\frac{8}{2^2}$
$latex =12-2$
$latex m=10$
Tenemos la ecuación $latex y=10x+b$. Usamos el punto (2, 4) para encontrar el valor de b:
$latex y=10x+b$
$latex 4=10(2)+b$
$latex b=-15$
La ecuación de la recta tangente en el punto (2, 4) es $latex y=10x-15$.
EJERCICIO 5
¿Cuál es la recta tangente a $latex f(x) = -x^{-2}+\sqrt{x}$ en el punto (1, 3)?
Solución
Empezamos encontrando la derivada de la función para determinar la pendiente de la recta tangente:
$latex f(x)=-x^{-2}+x^{\frac{1}{2}}$
$$f'(x)=2x^{-3}+\frac{1}{2}x^{-\frac{1}{2}}$$
$$f'(x)=\frac{2}{x^3}+\frac{1}{2\sqrt{x}}$$
La pendiente de la tangente en el punto (1, 3) es igual a $latex f'(1)$, por lo que, tenemos:
$$m=f'(1)=\frac{2}{(1)^3}+\frac{1}{2\sqrt{1}}$$
$latex =2+\frac{1}{2}$
$latex m=\frac{5}{2}$
Ahora que hemos formado la ecuación $latex y=\frac{5}{2}x+b$, usamos el punto (1, 3) para encontrar el valor de b:
$$y=\frac{5}{2}x+b$$
$$3=\frac{5}{2}(1)+b$$
$latex b=\frac{1}{2}$
La ecuación de la recta tangente en el punto (1, 3) es $latex y=\frac{5}{2}x+\frac{1}{2}$.
EJERCICIO 6
Si es que tenemos la función $latex f(x)=\sin(x)-\cos(x)$, ¿cuál es la ecuación de la recta tangente en el punto (0, 1)?
Solución
Empezamos encontrando la derivada de la función:
$latex f(x)=\sin(x)-\cos(x)$
$latex f'(x)=\cos(x)+\sin(x)$
Ahora, sabemos que la pendiente de la recta tangente en el punto (0, 1) es encontrada al evaluar $latex f'(0)$. Entonces, tenemos:
$latex m=f'(0)=\cos(0)+\sin(0)$
$latex m=1+0$
$latex m=1$
Hasta ahora, tenemos la ecuación $latex y=x+b$ y podemos usar esta ecuación con el punto (0, 1) para encontrar el valor de b, usando el punto (0, 1) en la ecuación:
$latex y=x+b$
$latex 1=0+b$
$latex b=1$
La ecuación de la recta tangente en el punto (0, 1) es $latex y=x+1$.
EJERCICIO 7
Encuentra la recta tangente a $latex f(x)=-2\sin(2x)+\cos(3x)$ en el punto (0, 1).
Solución
Necesitamos la derivada de la función para encontrar la pendiente de la tangente. Entonces, tenemos:
$latex f(x)=-2\sin(2x)+\cos(3x)$
$latex f'(x)=-4\cos(2x)-3\sin(3x)$
Ahora, podemos evaluar $latex f'(0)$ para determinar la pendiente de la recta tangente en el punto (0, 1):
$latex m=f'(0)=-4\cos(2(0))-3\sin(3(0))$
$latex m=-4+0$
$latex m=-4$
Usando la pendiente encontrada, tenemos la ecuación $latex y=-4x+b$. Al usar esta ecuación con el punto (0, 1) encontramos el valor de b:
$latex y=-4x+b$
$latex 1=0+b$
$latex b=1$
La ecuación de la recta tangente en el punto (0, 1) es $latex y=-4x+1$.
EJERCICIO 8
¿Cuál es la recta tangente a $latex f(x)=x^2-3x+1$ en el punto en donde la curva corta al eje y?
Solución
La derivada de la función es:
$latex f(x)=x^2-3x+1$
$latex f'(x)=2x-3$
El enunciado nos dice que tenemos que encontrar la recta tangente en el punto donde la curva corta al eje y. Esto sucede cuando las coordenadas en x son igual a 0. Entonces, tenemos:
$latex y=x^2-3x+1$
$latex y=0^2-3(0)+1$
$latex y=1$
Por lo tanto, el punto de la tangente es (0, 1). Ahora, evaluamos $latex f'(0)$ para encontrar la pendiente de la tangente y tenemos:
$latex m=f'(0)=2(0)-3$
$latex m=-3$
La pendiente encontrada nos da la ecuación $latex y=-3x+b$. Para encontrar el valor de b, usamos el punto (0, 1) en la ecuación:
$latex y=-3x+b$
$latex 1=-3(0)+b$
$latex b=1$
La ecuación de la recta tangente en el punto (0, 1) es $latex y=-3x+1$.
EJERCICIO 9
Encuentra las ecuaciones de las dos rectas tangentes a $latex f(x)=x^2-5x+4$ en los puntos en donde la función corta al eje x.
Solución
Los puntos en donde la función corta al eje x son los ceros de la función. Entonces, empezamos encontrando los ceros:
$latex x^2-5x+4=0$
$latex (x-4)(x-1)=0$
La función corta al eje x cuando $latex x=4$ y $latex x=1$. Además, los valores de y en esos puntos son 0, por lo que tenemos (4, 0) y (1, 0).
Ahora, encontramos la derivada y evaluamos $latex f'(4)$ y $latex f'(1)$ para determinar las pendientes de las rectas tangentes.
$latex f(x)=x^2-5x+4$
$latex f'(x)=2x-5$
$latex f'(4)=2(4)-5=3$
$latex f'(1)=2(1)-5=-3$
Ahora, encontramos los valores de b usando la forma $latex y=mx+b$ con las pendientes encontradas y las coordenadas de cada punto.
$latex 0=3(4)+b_{1}$
$latex b_{1}=-12$
$latex 0=-3(1)+b_{2}$
$latex b_{2}=3$
Entonces, las ecuaciones de las rectas tangentes son $latex y=3x-12$ y $latex y=-3x+3$.
EJERCICIO 10
Encuentra las dos rectas tangentes a la función $latex f(x)=x^2$ en los puntos en donde $latex y=9$.
Solución
El enunciado nos dice que las rectas son tangentes en los puntos en donde $latex y=9$. Entonces, tenemos que encontrar los valores de x cuando $latex y=9$:
$latex x^2=9$
$latex x=\pm \sqrt{9}$
$latex x=3~~$ o $latex ~~x=-3$
Ahora, usamos la derivada de la función para encontrar las pendientes de las rectas al evaluar $latex f'(3)$ y $latex f'(-3)$.
$latex f(x)=x^2$
$latex f'(x)=2x$
$latex f'(3)=2(3)=6$
$latex f'(-3)=2(-3)=-6$
Usando la forma $latex y=mx+b$ con las pendientes encontradas y las coordenadas de cada punto (los valores de y son 9 en ambos casos), podemos encontrar los valores de b:
$latex 9=6(3)+b_{1}$
$latex b_{1}=-9$
$latex 9=-6(-3)+b_{2}$
$latex b_{2}=-9$
Entonces, las ecuaciones de las rectas tangentes son $latex y=6x-9$ y $latex y=-6x-9$.
Ejercicios de recta tangente a una curva para resolver


Tenemos la función $latex f(x)=\frac{9}{x}$. Encuentra la recta tangente cuando $latex x=-3$.
Escribe la ecuación en la casilla.
Véase también
¿Interesado en aprender más sobre ecuaciones de rectas tangentes y normales a funciones? Puedes mirar estas páginas:


