Para encontrar la ecuación de la recta normal a una curva en un punto dado, tenemos que usar la forma y=mx+b en donde m es la pendiente y b es el intercepto en y. Además, la pendiente de la recta normal es encontrada usando la derivada de la función y recordando que la pendiente de la normal será igual a -1/m.
A continuación, exploraremos 10 ejercicios resueltos de la ecuación de la recta normal a una curva. Además, miraremos 5 problemas de práctica.
Cómo encontrar la ecuación de la recta normal a una curva
La recta norma a una curva en un punto P es la línea recta que pasa a través del punto P y que es perpendicular a la recta tangente a la curva en el punto P.
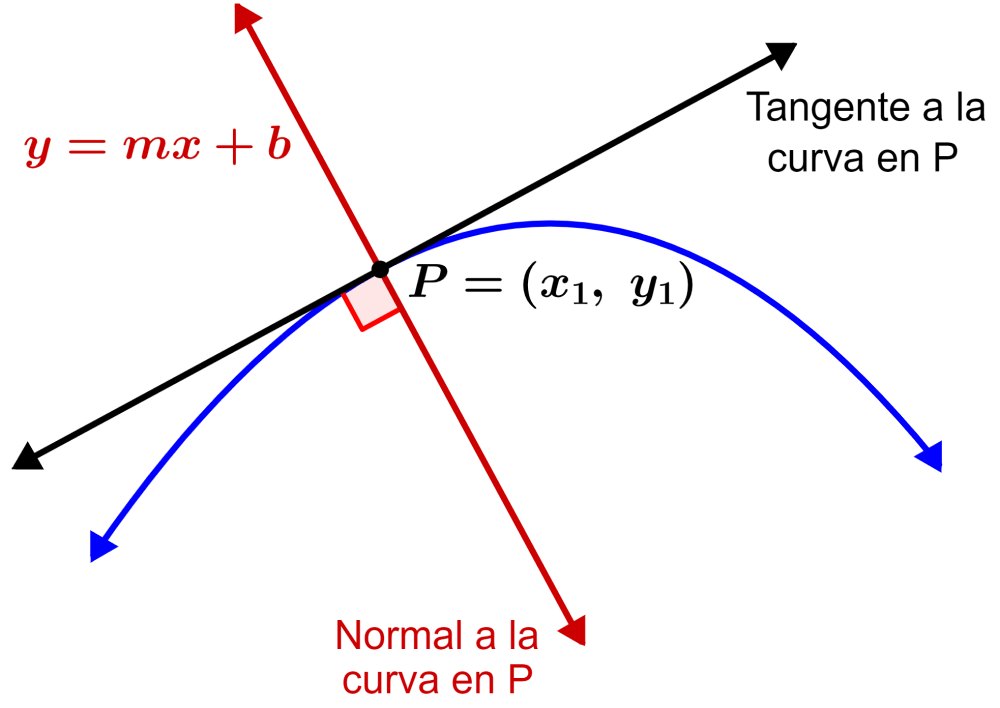
Dado que la tangente y la normal son perpendicular la una con la otra, si es que la pendiente de la tangente es $latex m$, entonces la pendiente de la normal es igual a $latex -\frac{1}{m}$.
Entonces, si es que queremos encontrar la ecuación de la recta normal a una curva en el punto $latex (x_{1},~y_{1})$, podemos seguir los siguientes pasos:
Paso 1: Obtener la derivada de la función que representa a la curva.
Paso 2: Encontrar la pendiente de la recta tangente a la curva en el punto $latex (x_{1},~y_{1})$. Para esto, usamos la coordenada en x del punto en la derivada de la función. Es decir, tenemos $latex m_{1}=f'(x_{1})$.
Paso 3: Usar la pendiente del paso 2 para encontrar la pendiente de la recta normal a la curva. La pendiente de la recta normal es igual a $latex m=-\frac{1}{m_{1}}$.
Paso 4: Sustituye la pendiente del paso 3 en la forma $latex y=mx+b$ y usa las coordenadas en x y en y del punto dado para encontrar el valor de b. Es decir, tenemos $latex y_{1}=mx_{1}=b$.
Paso 5: Usar los valores de m y b en la forma $latex y=mx+b$ para obtener la ecuación de la recta.
10 Ejercicios resueltos de la recta normal a una curva
EJERCICIO 1
Encuentra la ecuación de la recta normal a la función $latex f(x)=x^2$ en el punto P=(1, 2).
Solución
Podemos encontrar la ecuación de la recta normal usando la forma general $latex y=mx+b$, en donde m es la pendiente y b es el intercepto en y.
Ahora, la pendiente de la normal es igual a $latex -\frac{1}{m_{1}}$, en donde $latex m_{1}$ es la pendiente de la recta tangente. A su vez, la pendiente de la recta tangente es igual a $latex f'(1)$ (evaluamos la derivada en el punto dado). Entonces, tenemos:
$latex f(x)=x^2$
$latex f'(x)=2x$
$latex m_{1}=f'(1)=2(1)$
$latex m_{1}=2$
∴ $latex m=-\frac{1}{2}$
Esto significa que tenemos la ecuación $latex y=-\frac{1}{2}x+b$. Por lo tanto, usamos el punto (1, 2) en la ecuación para determinar el valor de b:
$latex y=-\frac{1}{2}x+b$
$latex 2=-\frac{1}{2}(1)+b$
$latex b=\frac{5}{2}$
La ecuación de la recta normal en el punto (1, 2) es $latex y=-\frac{1}{2}x+\frac{5}{2}$.
EJERCICIO 2
¿Cuál es la ecuación de la recta normal a la función $latex f(x)=x^3-6x$ en el punto (-1, 1)?
Solución
Para encontrar la ecuación de la recta normal, tenemos que empezar encontrando la derivada de la función. Entonces, tenemos:
$latex f(x)=x^3-6x$
$latex f'(x)=3x^2-6$
Ahora, podemos usar la derivada para encontrar la pendiente de la recta tangente en el punto (-1, 1) al evaluar $latex f'(-1)$:
$latex m_{1}=f'(-1)=3(-1)^2-6$
$latex m_{1}=-3$
La pendiente de la recta normal es igual a $latex m=\frac{1}{3}$. Entonces, tenemos la ecuación $latex y=\frac{1}{3}x+b$. Entonces, encontramos el valor de b, usando el punto (-1, 1) en la ecuación:
$latex y=\frac{1}{3}x+b$
$latex 1=\frac{1}{3}(-1)+b$
$latex b=\frac{4}{3}$
La ecuación de la recta normal en el punto (-1, 1) es $latex y=\frac{1}{3}x-\frac{4}{3}$.
EJERCICIO 3
Si es que tenemos la función $latex f(x)=2x^3-7x^2$, encuentra la recta normal en el punto (2, -3).
Solución
Empezamos encontrando la pendiente de la recta tangente. Para esto, obtenemos la derivada de la función:
$latex f(x)=2x^3-7x^2$
$latex f'(x)=6x^2-14x$
La pendiente de la recta tangente en el punto (2, 3) es dada por $latex f'(2)$:
$latex m_{1}=f'(2)=6(2)^2-14(2)$
$latex m_{1}=24-28$
$latex m_{1}=-4$
La pendiente de la recta normal es $latex m=\frac{1}{4}$. Entonces, tenemos la ecuación $latex y=\frac{1}{4}x+b$. Ahora, usamos esta ecuación con el punto (2, -3) para encontrar el valor de b:
$latex y=\frac{1}{4}x+b$
$latex -3=\frac{1}{4}(2)+b$
$latex b=-\frac{7}{2}$
La ecuación de la recta normal en el punto (2, -3) es $latex y=\frac{1}{4}x-\frac{7}{2}$.
EJERCICIO 4
Encuentra la ecuación de la recta normal a la función $latex f(x)=x^3+\frac{6}{x}$ en el punto (1, -2).
Solución
La derivada de la función es:
$latex f(x)=x^3+6x^{-1}$
$latex f'(x)=3x^2-6x^{-2}$
$latex f'(x)=3x^2-\frac{6}{x^2}$
Ahora, usamos la derivada para encontrar la pendiente de la tangente en el punto (1, -2). Esto es igual a $latex f'(1)$:
$latex m_{1}=f'(1)=3(1)^2-\frac{6}{1^2}$
$latex =3-6$
$latex m_{1}=-3$
La pendiente de la recta normal es $latex m=\frac{1}{3}$. Entonces, tenemos la ecuación $latex y=\frac{1}{3}x+b$. Luego, usamos el punto (1, -2) para encontrar el valor de b:
$latex y=\frac{1}{3}x+b$
$latex -2=\frac{1}{3}(1)+b$
$latex b=-\frac{7}{3}$
La ecuación de la recta normal en el punto (1, -2) es $latex y=\frac{1}{3}x-\frac{7}{3}$.
EJERCICIO 5
Encuentra la recta normal a $latex f(x) = -x^{-2}+\sqrt{x}$ en el punto (1, -2).
Solución
Tenemos que empezar encontrando la derivada de la función dada:
$latex f(x)=-x^{-2}+x^{\frac{1}{2}}$
$$f'(x)=2x^{-3}+\frac{1}{2}x^{-\frac{1}{2}}$$
$$f'(x)=\frac{2}{x^3}+\frac{1}{2\sqrt{x}}$$
Ahora, usamos la derivada para encontrar la pendiente de la tangente en el punto (1, -2). Esto es igual a $latex f'(1)$:
$$m_{1}=f'(1)=\frac{2}{(1)^3}+\frac{1}{2\sqrt{1}}$$
$latex =2+\frac{1}{2}$
$latex m_{1}=\frac{5}{2}$
La pendiente de la recta normal es $latex m=-\frac{2}{5}$. Entonces, tenemos la ecuación $latex y=-\frac{2}{5}x+b$, por lo que usamos el punto (1, -2) para encontrar el valor de b:
$$y=-\frac{2}{5}x+b$$
$$-2=-\frac{2}{5}(1)+b$$
$latex b=-\frac{8}{5}$
La ecuación de la recta normal en el punto (1, -2) es $latex y=-\frac{2}{5}x-\frac{8}{5}$.
EJERCICIO 6
Encuentra la recta normal a la función $latex f(x)=\sin(x)-\cos(x)$ en el punto (0, 1).
Solución
La derivada de la función es:
$latex f(x)=\sin(x)-\cos(x)$
$latex f'(x)=\cos(x)+\sin(x)$
La pendiente de la recta tangente en el punto (0, 1) es igual a $latex f'(0)$. Entonces, tenemos:
$latex m_{1}=f'(0)=\cos(0)+\sin(0)$
$latex m_{1}=1+0$
$latex m_{1}=1$
La pendiente de la recta normal es igual a $latex m=-1$. Entonces, tenemos la ecuación $latex y=-x+b$ y ahora usamos esta ecuación con el punto (0, 1) para encontrar el valor de b:
$latex y=-x+b$
$latex 1=-0+b$
$latex b=1$
La ecuación de la recta normal en el punto (0, 1) es $latex y=-x+1$.
EJERCICIO 7
¿Cuál es la ecuación de la recta normal a la función $latex f(x)=-2\sin(2x)+\cos(3x)$ en el punto (0, 1)?
Solución
La derivada de la función es:
$latex f(x)=-2\sin(2x)+\cos(3x)$
$latex f'(x)=-4\cos(2x)-3\sin(3x)$
Usando la derivada, podemos encontrar la pendiente de la recta tangente en (0, 1) al evaluar $latex f'(0)$:
$latex m_{1}=f'(0)=-4\cos(2(0))-3\sin(3(0))$
$latex m_{1}=-4+0$
$latex m_{1}=-4$
La pendiente de la recta normal es $latex m=\frac{1}{4}$. Entonces, tenemos la ecuación $latex y=\frac{1}{4}x+b$. Ahora, usamos esta ecuación con el punto (0, 1) para determinar el valor de b:
$latex y=\frac{1}{4}x+b$
$latex 1=0+b$
$latex b=1$
La ecuación de la recta normal en el punto (0, 1) es $latex y=\frac{1}{4}x+1$.
EJERCICIO 8
Encuentra la recta normal a $latex f(x)=x^2-3x+1$ en el punto en donde la curva corta al eje y.
Solución
Empezamos encontrando la derivada de la función:
$latex f(x)=x^2-3x+1$
$latex f'(x)=2x-3$
No conocemos las coordenadas del punto directamente, pero sabemos que la recta es normal en el punto donde la curva corta al eje y. Esto sucede cuando las coordenadas en x son igual a 0. Entonces, tenemos:
$latex y=x^2-3x+1$
$latex y=0^2-3(0)+1$
$latex y=1$
Por lo tanto, el punto es (0, 1). Ahora, usamos la derivada de la función para evaluar $latex f'(0)$ y encontrar la pendiente de la tangente:
$latex m_{1}=f'(0)=2(0)-3$
$latex m_{1}=-3$
La pendiente de la recta normal es $latex m=\frac{1}{3}$. Entonces, tenemos la ecuación $latex y=\frac{1}{3}x+b$. Usando el punto (0, 1) encontramos el valor de b:
$latex y=\frac{1}{3}x+b$
$latex 1=\frac{1}{3}(0)+b$
$latex b=1$
La ecuación de la recta normal en el punto (0, 1) es $latex y=\frac{1}{3}x+1$.
EJERCICIO 9
Encuentra las ecuaciones de las dos rectas normales a la función $latex f(x)=x^2-5x+4$ en los puntos en donde la función corta al eje x.
Solución
Tenemos que empezar encontrando los puntos en donde la función corta al eje x. Esto sucede cuando el valor de y es 0. Entonces, tenemos:
$latex x^2-5x+4=0$
$latex (x-4)(x-1)=0$
La función corta al eje x cuando $latex x=4$ y $latex x=1$. Esto significa que tenemos los puntos (4, 0) y (1, 0).
Ahora, usamos la derivada de la función para encontrar las pendientes de las rectas tangentes al evaluar $latex f'(4)$ y $latex f'(1)$:
$latex f(x)=x^2-5x+4$
$latex f'(x)=2x-5$
$latex f'(4)=2(4)-5=3$
$latex f'(1)=2(1)-5=-3$
Las pendientes de las rectas normales son $latex m_{1}=-\frac{1}{3}$ y $latex m_{2}=\frac{1}{3}$. Entonces, usamos la forma $latex y=mx+b$ con las pendientes encontradas y las coordenadas de cada punto para determinar los valores de b:
$latex 0=\frac{1}{3}(4)+b_{1}$
$latex b_{1}=-\frac{4}{3}$
$latex 0=-\frac{1}{3}(1)+b_{2}$
$latex b_{2}=\frac{1}{3}$
Entonces, las ecuaciones de las rectas normales son $latex y=-\frac{1}{3}x-\frac{4}{3}$ y $latex y=\frac{1}{3}x+\frac{1}{3}$.
EJERCICIO 10
Encuentra las dos rectas normales a la función $latex f(x)=x^2$ en los puntos en donde $latex y=9$.
Solución
Tenemos que las rectas son normales en los puntos en donde $latex y=9$. Esto significa que tenemos que encontrar los valores de x cuando $latex y=9$:
$latex x^2=9$
$latex x=\pm \sqrt{9}$
$latex x=3~~$ o $latex ~~x=-3$
Ahora que conocemos las coordenadas de los puntos, usamos la derivada de la función para encontrar las pendientes de las rectas tangentes al evaluar $latex f'(3)$ y $latex f'(-3)$.
$latex f(x)=x^2$
$latex f'(x)=2x$
$latex f'(3)=2(3)=6$
$latex f'(-3)=2(-3)=-6$
Las pendientes de las rectas normales son $latex m_{1}=-\frac{1}{6}$ y $latex m_{2}=\frac{1}{6}$.
Ahora, usamos la forma $latex y=mx+b$ con las pendientes encontradas y las coordenadas de cada punto (los valores de y son 9 en ambos casos) para encontrar los valores de b:
$latex 9=-\frac{1}{6}(3)+b_{1}$
$latex b_{1}=\frac{19}{2}$
$latex 9=\frac{1}{6}(-3)+b_{2}$
$latex b_{2}=\frac{19}{2}$
Entonces, las ecuaciones de las rectas normales son $latex y=-\frac{1}{6}x+\frac{19}{2}$ y $latex y=\frac{1}{6}x+\frac{19}{2}$.
Ejercicios de recta normal a una curva para resolver
¿Cuál es la ecuación de la recta normal a la función $latex f(x)=2\sqrt{x}$ en donde $latex x=9$?
Escribe la ecuación en la casilla.
Véase también
¿Interesado en aprender más sobre ecuaciones de rectas tangentes y normales a funciones? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
