Las parábolas son definidas como secciones cónicas que son formadas al cortar a un cono con un plano que es paralelo a un lado del cono. Las parábolas son formadas por el conjunto de todos los puntos que son equidistantes con respecto a una línea, llamada la directriz, y a un punto, llamado el foco.
A continuación, aprenderemos cómo definir una ecuación de la parábola. Veremos dos casos diferentes: cuando el vértice de la parábola se ubica en el origen y cuando el vértice se ubica fuera del origen. Aplicaremos lo aprendido al resolver algunos ejercicios.
PRECÁLCULO
Relevante para…
Aprender sobre las ecuaciones de las parábolas con ejemplos.
PRECÁLCULO
Relevante para…
Aprender sobre las ecuaciones de las parábolas con ejemplos.
Parábolas que tienen el vértice en (0, 0)
Una forma de definir a las parábolas es usando la ecuación general $latex y={{x}^2}$. Esta ecuación representa a una parábola con un vértice en el origen, (0, 0), y un eje de simetría en $latex x=0$.
Adicionalmente, también podemos usar al foco y a la directriz de la parábola para obtener una ecuación, ya que cada punto en la parábola es equidistante al foco y a la directriz.
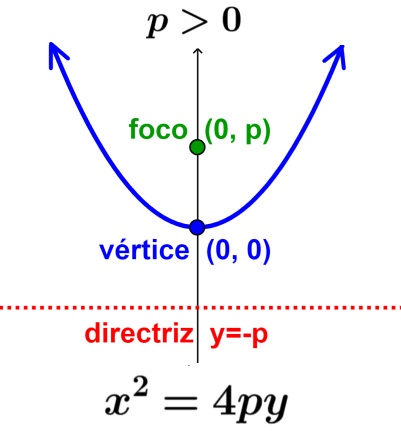
El vértice de la parábola está ubicado en la mitad entre el foco y la directriz. El foco es un punto que se ubica en el eje de simetría, mientras que la directriz es una línea que es perpendicular con respecto al eje de simetría. La siguiente imagen muestra al foco, al vértice y a la directriz:
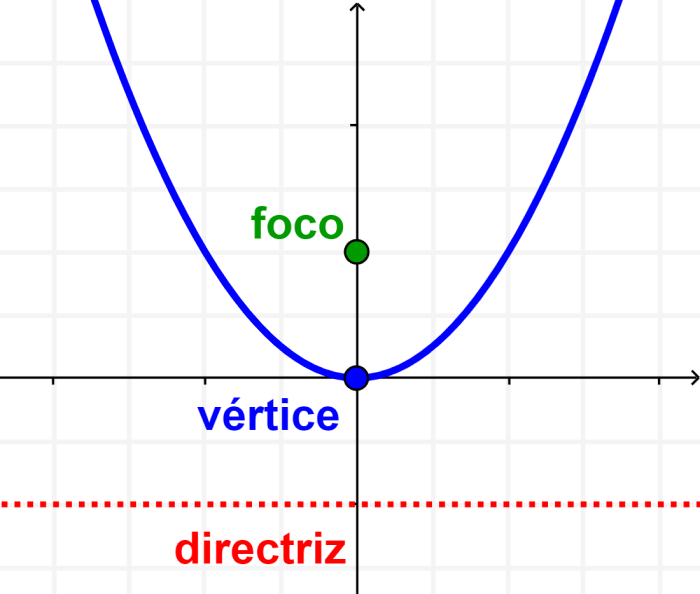
Sabemos que podemos describir a una parábola usando la forma general $latex y=a{{x}^2}$. Es posible reescribir a esta ecuación usando la forma $latex {{x}^2}=4py$, en donde p es una constante usada para encontrar el foco y la directriz.
Esto corresponde a una parábola con orientación vertical. Por otra parte, cuando tenemos una parábola con orientación horizontal, tenemos la ecuación $latex {{y}^2}=4px$.
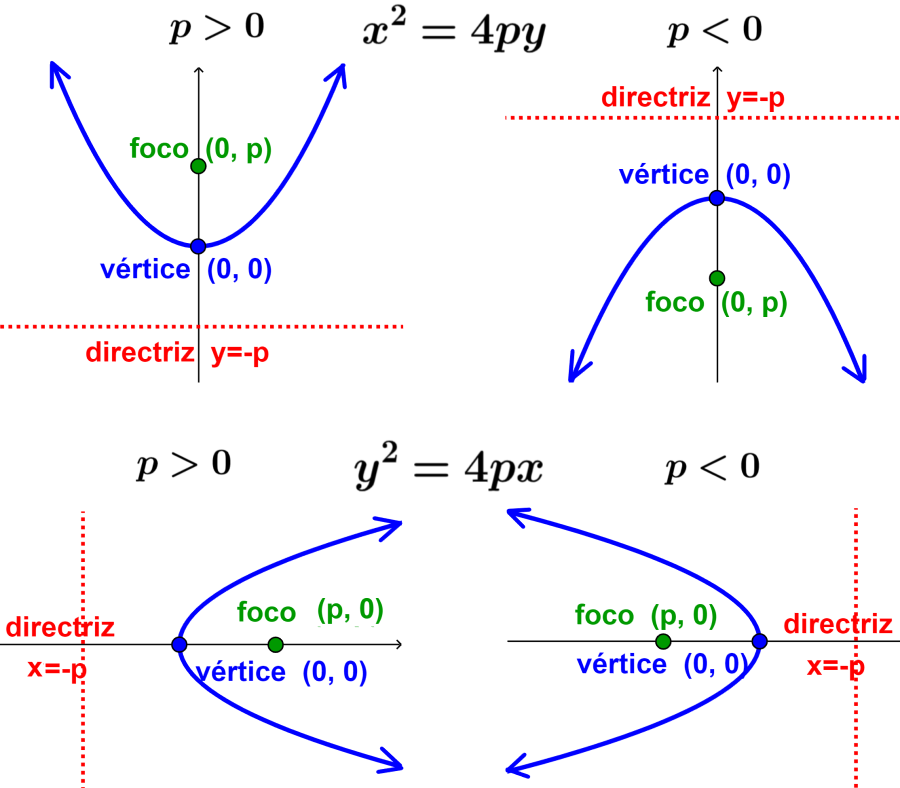
El diagrama nos muestra los cuatro casos diferentes que podemos tener cuando la parábola tiene un vértice en (0, 0). Cuando la variable x es elevada al cuadrado, la parábola está orientada verticalmente y cuando la variable y es elevada al cuadrado, la parábola está orientada horizontalmente.
Además, cuando el valor de p es positivo, la parábola se abre hacia la parte positiva de los ejes, es decir, hacia arriba o hacia la derecha. Por otra parte, cuando el valor de p es negativo, la parábola se abre hacia la parte negativa de los ejes, es decir, hacia abajo o hacia la izquierda.
EJERCICIO 1
¿Cuál es la ecuación de una parábola que tiene un foco en (0, 3)?
Solución
Sabemos que el vértice de la parábola está ubicado en (0, 0). El hecho que el foco está en (0, 3) indica que el valor de p es el valor de y y es positivo. Esto significa que la parábola se abrirá hacia arriba.
Entonces, la ecuación general es $latex {{x}^2}=4py$.
Al sustituir a p por 3, tenemos:
$latex {{x}^2}=4(3)y$
$latex {{x}^2}=12y$
EJERCICIO 2
Si es que tenemos la parábola $latex y=\frac{1}{2}{{x}^2}$, ¿cuál es su foco y su directriz?
Solución
Encontramos el foco y la directriz al despejar a $latex {{x}^2}$ y determinar el valor de p. Entonces, tenemos:
$latex y=\frac{1}{2}{{x}^2}$
$latex 2y={{x}^2}$
Podemos formar la ecuación $latex 2=4p$ y resolver para p:
$latex 2=4p$
$latex p=\frac{1}{2}$
Entonces, el foco es $latex (0, \frac{1}{2})$ y la directriz es $latex y=-\frac{1}{2}$.
Parábolas que tienen el vértice en (h, k)
No todas las parábolas tienen su vértice en el punto (0, 0) ya que en muchas ocasiones, las parábolas tienen a su vértice en el punto $latex (h, k)$ que se ubica fuera del origen.
Arriba vimos que, cuando el vértice de la parábola está ubicado en el origen, su ecuación es $latex {{x}^2}=4py$ o $latex {{y}^2}=4px$ dependiendo en su orientación.
Si es que combinamos estas ecuaciones con la forma vértice de las parábolas, $latex y=a{{(x-h)}^2}-k$, podemos formar una ecuación que aplica para casos cuando el vértice no está en el origen.
Entonces, empezamos despejando a $latex {{(x-h)}^2}$:
$latex y=a{{(x-h)}^2}-k$
$latex {{(x-h)}^2}=\frac{1}{a}(y-k)$
Si es que comparamos a esta ecuación con $latex {{x}^2}=4py$, tenemos $latex 4p=\frac{1}{a}$. Entonces:
$latex {{(x-h)}^2}=4p(y-k)$
Esta es la ecuación de una parábola orientada verticalmente. Por otra parte, si es que la parábola está orientada horizontalmente, su ecuación será $latex {{(y-k)}^2}=4p(x-h)$.
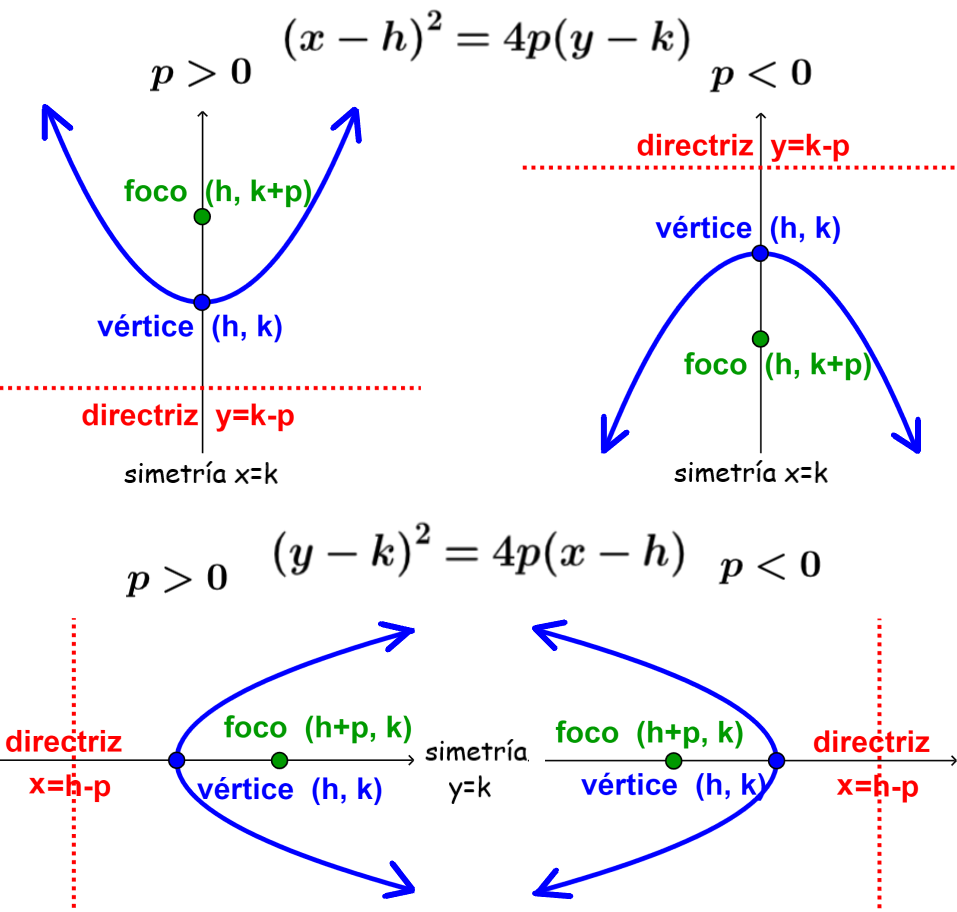
El diagrama nos muestra que, cuando la variable x está elevada al cuadrado, la parábola está orientada verticalmente y cuando la variable y está elevada al cuadrado, la parábola está orientada horizontalmente.
Además, el valor de p indica hacia dónde se abre la parábola. Si es que p es positivo, la parábola se abre hacia la parte positiva de los ejes. Si es que p es negativo, la parábola se abre hacia la parte negativa de los ejes.
EJERCICIO 1
Si es que el vértice de una parábola está ubicado en (-2, 4) y su directriz es $latex y=7$, ¿cuál es su ecuación?
Solución
Vemos que la directriz es una línea horizontal, por lo que la parábola está orientada verticalmente y se abrirá hacia arriba o hacia abajo.
Además, también vemos que la directriz está ubicada encima del vértice, por lo que la parábola se abre hacia abajo y el valor de p es negativo.
Podemos encontrar el valor de p usando el vértice $latex (h, k)$. La ecuación para una directriz horizontal es $latex y=k-p$. Entonces, tenemos:
$latex 7=4-p$
$latex 3=-p$
$latex p=-3$
Usando estos valores, tenemos:
$latex {{(x-h)}^2}=4p(y-k)$
$latex {{(x-(-2))}^2}=4(-3)(y-4)$
$latex {{(x+2)}^2}=-12(y-4)$
EJERCICIO 2
¿Cuál es el vértice, el foco, el eje de simetría y la directriz de la parábola $latex {{(x+3)}^2}=4(y+4)$?
Solución
Podemos comparar a esta ecuación con la ecuación general dada arriba. Entonces, el vértice es el punto $latex (-3, -4)$. Además, dado que la variable x está elevada al cuadrado, la parábola se abre hacia arriba.
Ahora, formamos la ecuación $latex 4p=4$. Resolviendo para p, tenemos $latex p=1$. Esto significa que, el foco es $latex (-3, -4+1)=(-3, -3)$, el eje de simetría es $latex x=-3$ y la directriz es $latex y=-3-1=-4$.
Véase también
¿Interesado en aprender más sobre parábolas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
