Una parábola es una sección cónica formada cuando un cono circular es cortado por un plano. Para que la parábola sea formada, el plano que corta al cono debe ser paralelo a un lado del cono. Una parábola está definida por el conjunto de todos los puntos (x, y) que están ubicados a la misma distancia desde una línea, llamada la directriz, y un punto fijo (el foco) que no está en la directriz.
A continuación, conoceremos un poco sobre estas secciones cónicas y aprenderemos sobre la ecuación de la parábola cuando el vértice se ubica en el origen. Resolveremos algunos ejercicios para aplicar estos conceptos.
PRECÁLCULO
Relevante para…
Aprender sobre la ecuación de la parábola que tiene vértice en el origen.
PRECÁLCULO
Relevante para…
Aprender sobre la ecuación de la parábola que tiene vértice en el origen.
Parábolas con vértice en el origen
De álgebra, sabemos que una parábola tiene la ecuación general $latex y={{x}^2}$. La gráfica de esta parábola tiene al vértice en (0, 0) y un eje de simetría en $latex x=0$.
Sin embargo, también es posible definir a una parábola en una manera diferente, ya que las parábolas tienen la propiedad principal de que cada punto en la parábola es equidistante desde otro punto, llamado el foco, y una línea llamada la directriz.
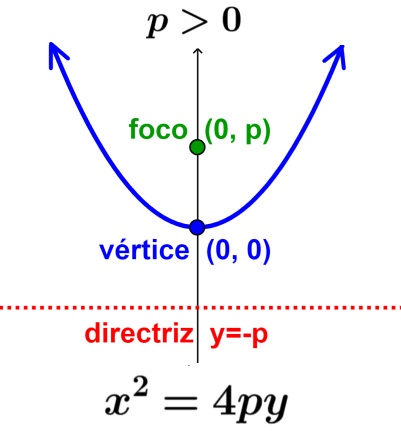
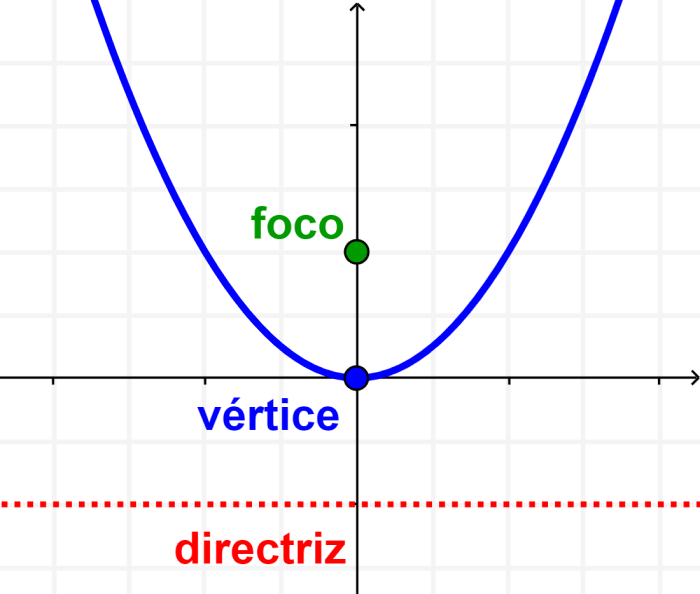
El foco de la parábola se ubica en su eje de simetría y el vértice está en la mitad entre el foco y la directriz. Además, la directriz es perpendicular con respecto al eje de simetría. Podemos observar esto en el siguiente diagrama:
La ecuación más común para describir a una parábola es en la forma $latex y=a{{x}^2}$. Vamos a reescribir a esta ecuación para obtener una ecuación de la forma $latex {{x}^2}=4py$, en donde p es usada para encontrar el foco y la directriz.
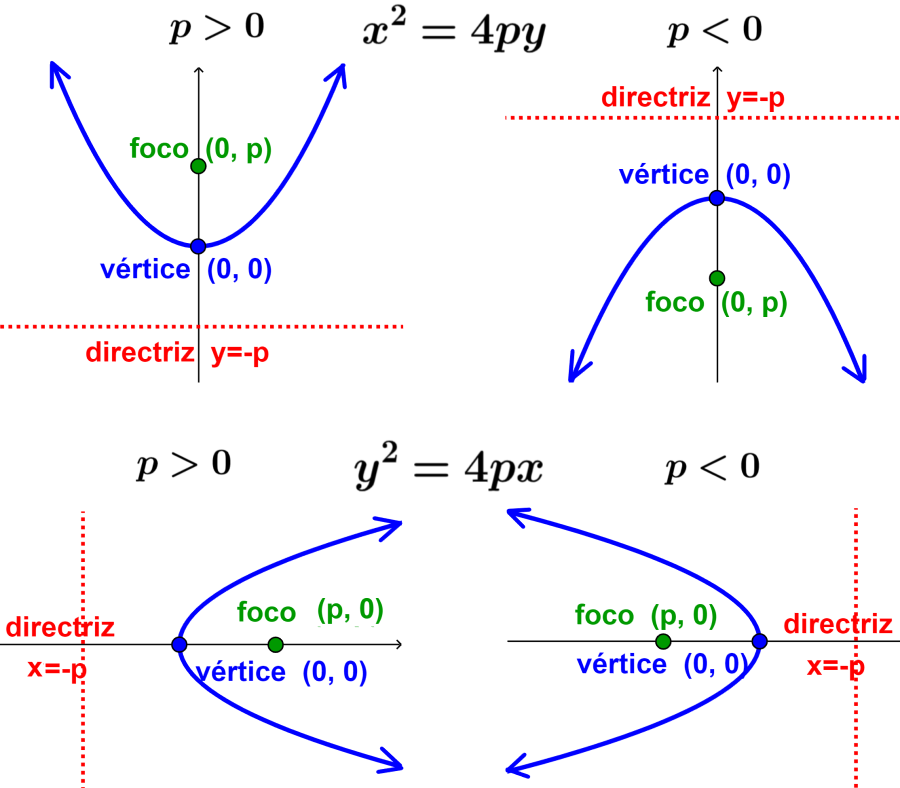
Además, también trazaremos a una parábola con orientación horizontal de modo que la ecuación será $latex {{y}^2}=4px$.
En los diagramas podemos ver que, en todos los casos el vértice es (0, 0). Cuando la parábola se abre hacia arriba o hacia abajo, vemos que la x es elevada al cuadrado. Por otra parte, cuando la parábola se abre hacia la izquierda o hacia la derecha, la y es elevada al cuadrado.
Además, cuando el valor de p es positivo, el foco se ubica en la parte positiva de los ejes y la parábola se abre hacia arriba o hacia la derecha. Por otra parte, cuando el valor de p es negativo, el foco se ubica en la parte negativa de los ejes y la parábola se abre hacia abajo o hacia la izquierda.
Gráficas de parábolas con vértice en el origen en su forma estándar
Vamos a encontrar el foco y la directriz de la parábola $latex {{y}^2}=-8x$. Además, vamos a determinar si es que la parábola se abre hacia arriba, abajo, izquierda o derecha. Luego, graficaremos a la parábola.
Para encontrar el foco y la directriz, tenemos que empezar encontrando p. Podemos formar la ecuación $latex -8=4p$ y resolver para p:
$latex -8=4p$
$latex p=-2$
Tenemos a y elevada al cuadrado, por lo que sabemos que la parábola se abre hacia la izquierda o hacia la derecha. Además, debido a que p es negativo, sabemos que la parábola debe abrirse hacia el lado negativo del eje x. Entonces, el foco es (-2, 0) y la directriz es $latex x=2$.
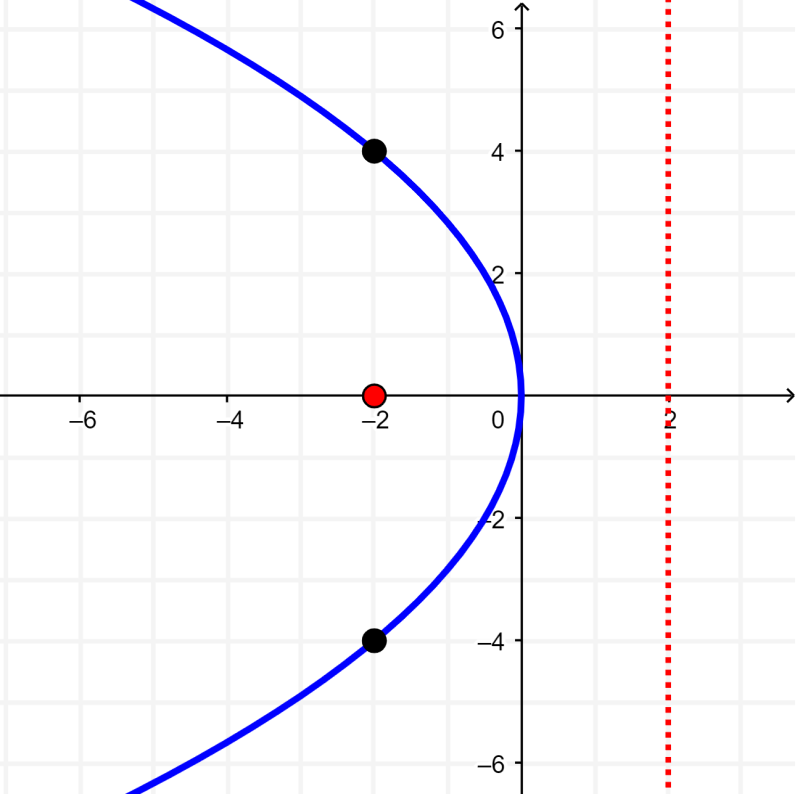
Para graficar a la parábola, tenemos que trazar al foco y a la directriz. Luego, encontramos por lo menos dos puntos en la parábola para lograr que la curva sea correcta.
En este caso, debido a que el punto (-2, 4) es parte de la parábola, el punto (-2, -4) también es parte de la parábola, ya que es simétrica. Entonces, tenemos:
Ejercicios de ecuaciones de parábolas resueltos
Los siguientes ejercicios son resueltos aplicando lo aprendido sobre ecuaciones de parábolas en su forma estándar. Estos ejercicios pueden ser usados para reforzar lo aprendido.
EJERCICIO 1
Si es que el foco de la parábola es (0, 2), ¿cuál es su ecuación?
Solución
El vértice de la parábola es (0, 0). Esto significa que el valor de p es el valor de y y es positivo, por lo que la parábola se abrirá hacia arriba. Entonces, la ecuación general es $latex {{x}^2}=4py$.
Si es que sustituimos a p por 2, tenemos:
$latex {{x}^2}=4(2)y$
$latex {{x}^2}=8y$
EJERCICIO 2
¿Cuál es el foco y la directriz de la parábola $latex y=\frac{1}{2}{{x}^2}$?
Solución
Para encontrar el foco y la directriz, tenemos que resolver para $latex {{x}^2}$ y luego encontrar p. Entonces, tenemos:
$latex y=\frac{1}{2}{{x}^2}$
$latex 2y={{x}^2}$
Ahora, formamos la ecuación $latex 2=4p$ y resolvemos para p:
$latex 2=4p$
$latex p=\frac{1}{2}$
Entonces, el foco es $latex (0, \frac{1}{2})$ y la directriz es $latex y=-\frac{1}{2}$.
EJERCICIO 3
Encuentra la ecuación de la parábola con directriz $latex x=-2$.
Solución
Si es que la directriz es negativa y vertical, sabemos que la ecuación tiene que ser $latex {{y}^2}=4px$ y que la parábola debe abrirse hacia la derecha, por lo que p es positivo: $latex p=2$. Entonces, la ecuación de la parábola es:
$latex {{y}^2}=4(2)x$
$latex {{y}^2}=8x$
Véase también
¿Interesado en aprender más sobre parábolas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
