Una elipse es definida como el conjunto de todos los puntos (x, y) en un plano de modo que, la suma de sus distancias desde dos puntos fijos es constante. Cada punto fijo es llamado un foco de la elipse. Todas las elipses tienen dos ejes de simetría. El eje más largo es llamado el eje mayor y el eje más corto es llamado el eje menor. Cada punto extremo del eje mayor es el vértice de la elipse y cada punto extremo del eje menor es el covértice de la elipse. El centro de una elipse es el punto medio tanto del eje mayor como del eje menor. Los ejes de la elipse son perpendiculares en el centro. Los focos siempre se ubican en el eje mayor.
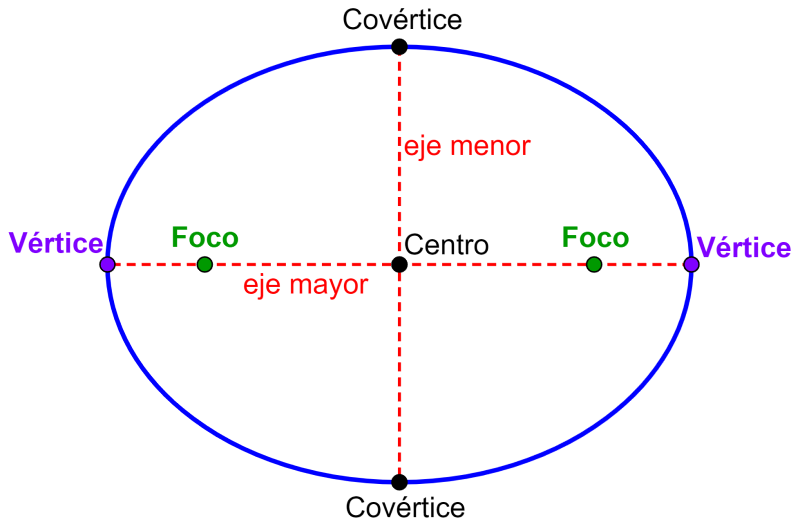
En este artículo, conoceremos la ecuación de la elipse centrada en el origen. Solo nos enfocaremos en las elipses que están posicionadas vertical u horizontalmente en el plano cartesiano.
Forma estándar de elipses centradas en el origen
Las formas estándar de ecuaciones nos dan información sobre las características principales de las gráficas. Las características principales de la elipse son su centro, vértices, covértices, focos y longitudes y posiciones del eje mayor y el eje menor.
Existen cuatro variaciones de la forma estándar de elipses. Estas variaciones dependen primeramente en la ubicación del centro (en el origen o fuera del origen) y luego en la posición de la elipse (vertical u horizontal).
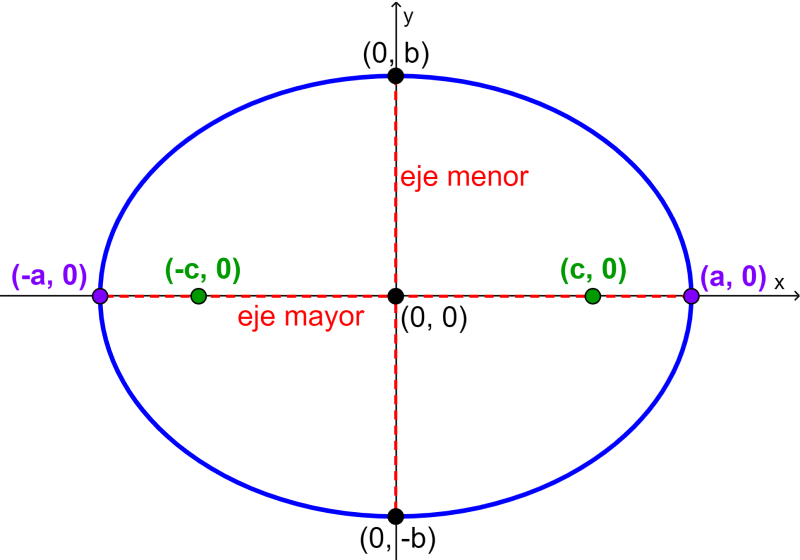
Ecuación de la elipse horizontal
La forma estándar de una elipse con centro en el origen, (0, 0), y con el eje mayor paralelo al eje x es:
| $latex \frac{{{x}^2}}{{{a}^2}}+\frac{{{y}^2}}{{{b}^2}}=1$ |
en donde,
- $latex a>b$
- La longitud del eje mayor es $latex 2a$
- La longitud del eje menor es $latex 2b$
- Las coordenadas de los vértices son $latex (\pm a, 0)$
- Las coordenadas de los covértices son $latex (0, \pm b)$
- Las coordenadas de los focos son $latex (\pm c, 0)$, en donde, $latex {{c}^2}={{a}^2}-{{b}^2}$
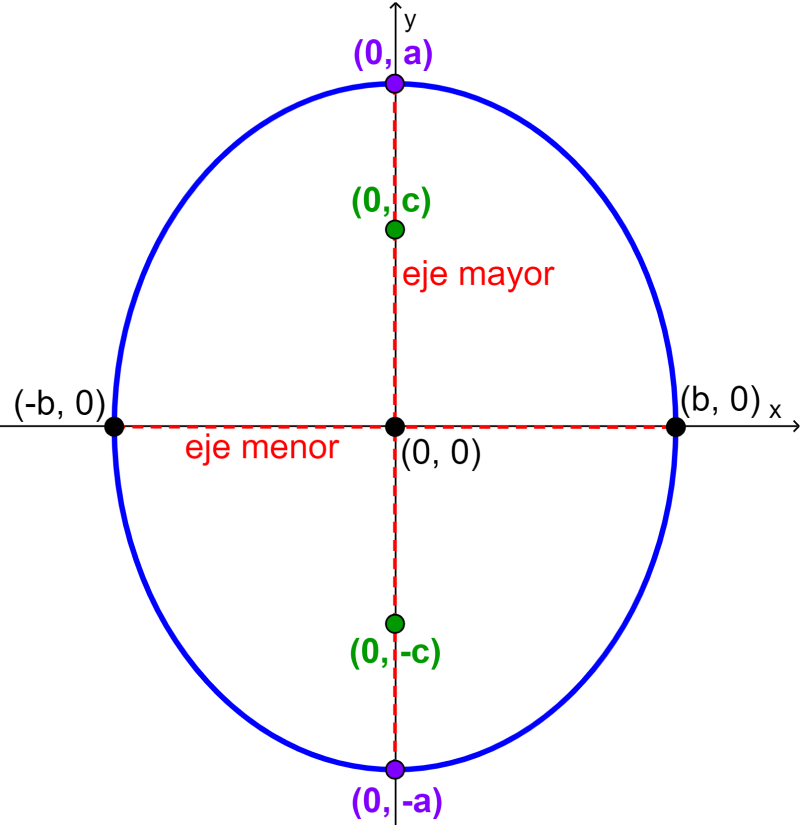
Ecuación de la elipse vertical
La ecuación de una elipse en su forma estándar que tiene al centro en el origen, (0, 0), y en la que su eje mayor es paralelo al eje y es:
| $latex \frac{{{x}^2}}{{{b}^2}}+\frac{{{y}^2}}{{{a}^2}}=1$ |
en donde,
- $latex a>b$
- El eje mayor mide $latex 2a$
- El eje menor mide $latex 2b$
- Las coordenadas de los vértices son $latex (0, \pm a)$
- Las coordenadas de los covértices son $latex (\pm b, 0)$
- Las coordenadas de los focos son $latex (0, \pm c)$, en donde, $latex {{c}^2}={{a}^2}-{{b}^2}$
Escribir la ecuación de elipses centradas en el origen usando los vértices y los focos
Para encontrar la ecuación de una elipse centrada en el origen dadas las coordenadas de los vértices y los focos, podemos seguir los siguientes pasos:
Paso 1: Determina si es que el eje mayor se ubica en el eje x o en el eje y.
1.1. Si es que las coordenadas de los vértices tienen la forma $latex (\pm a, 0)$ y las coordenadas de los focos tienen la forma $latex (\pm c, 0)$, entonces, el eje mayor es paralelo al eje x y usamos la ecuación $latex \frac{{{x}^2}}{{{a}^2}}+\frac{{{y}^2}}{{{b}^2}}=1$.
1.2. Si es que las coordenadas de los vértices tienen la forma $latex (0, \pm a)$ y las coordenadas de los focos tienen la forma $latex (0, \pm c)$, entonces, el eje mayor es paralelo al eje y y usamos la ecuación $latex \frac{{{x}^2}}{{{b}^2}}+\frac{{{y}^2}}{{{a}^2}}=1$.
Paso 2: Usamos la ecuación $latex {{c}^2}={{a}^2}-{{b}^2}$ junto con las coordenadas de los vértices y los focos y resolvemos para $latex {{b}^2}$.
Paso 3: Reemplazamos los valores de $latex {{a}^2}$ y $latex {{b}^2}$ en la ecuación obtenida en el paso 1.
Ejercicios resueltos de ecuación de la elipse con centro en el origen
Los siguientes ejercicios ponen en práctica lo aprendido sobre la ecuación de elipses que tienen a su centro en el origen. Analiza cada ejercicio para entender el proceso usado para obtener la respuesta.
EJERCICIO 1
Encuentra la ecuación de la elipse que tiene vértices en $latex (\pm 7, 0)$ y focos en $latex (\pm 4, 0)$.
Solución
Los focos se encuentran en el eje x, por lo que el eje mayor se encuentra en el eje x. Esto significa que la ecuación tendrá la siguiente forma:
$latex \frac{{{x}^2}}{{{a}^2}}+\frac{{{y}^2}}{{{b}^2}}=1$
Los vértices son $latex (\pm 7, 0)$, por lo que $latex a=7$ y tenemos $latex {{a}^2}=64$.
Los focos son $latex (\pm 4, 0)$, por lo que $latex c=4$ y tenemos $latex {{c}^2}=16$.
Ahora, usamos la ecuación $latex {{c}^2}={{a}^2}-{{b}^2}$ para obtener el valor de $latex {{b}^2}$. Entonces, tenemos:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex 16=64-{{b}^2}$
$latex {{b}^2}=48$
Tenemos que sustituir a los valores obtenidos en la ecuación estándar. Entonces, la ecuación de la elipse es:
$latex \frac{{{x}^2}}{64}+\frac{{{y}^2}}{48}=1$
EJERCICIO 2
¿Cuál es la ecuación de la elipse que tiene vértices en $latex (0, \pm 9)$ y focos en $latex (0, \pm 6)$?
Solución
En este caso, los focos se encuentran en el eje y. Esto significa que el eje mayor se encuentra en el eje y. Entonces, la ecuación tendrá la siguiente forma:
$latex \frac{{{x}^2}}{{{b}^2}}+\frac{{{y}^2}}{{{a}^2}}=1$
Los vértices son $latex (0, \pm 9)$, por lo que $latex a=9$ y tenemos $latex {{a}^2}=81$.
Los focos son $latex (0, \pm 6)$, por lo que $latex c=6$ y tenemos $latex {{c}^2}=64$.
Usando la ecuación $latex {{c}^2}={{a}^2}-{{b}^2}$, podemos obtener el valor de $latex {{b}^2}$. Entonces, tenemos:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex 64=81-{{b}^2}$
$latex {{b}^2}=17$
Usando estos valores, tenemos la siguiente ecuación de la elipse:
$latex \frac{{{x}^2}}{17}+\frac{{{y}^2}}{81}=1$
Ejercicios de ecuación de la elipse con centro en el origen para resolver
Pon en práctica lo aprendido para resolver los siguientes ejercicios. Encuentra las ecuaciones de las elipses con la información dada. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre elipses? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
