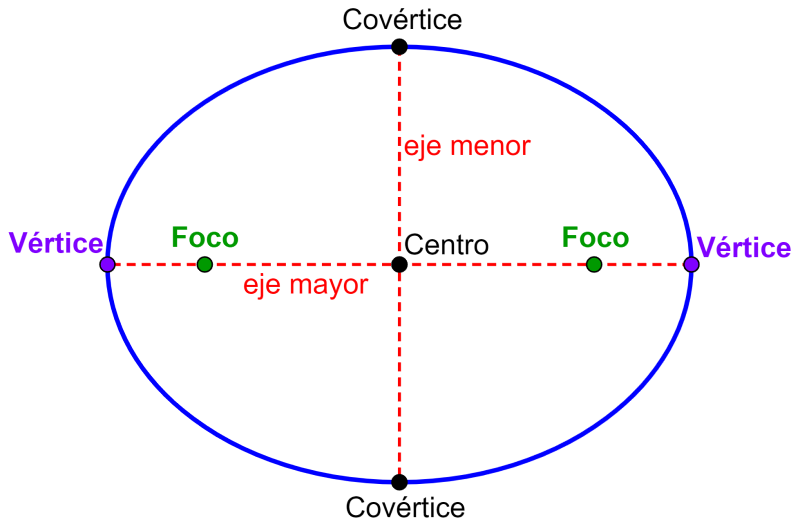
Las elipses son formadas por el conjunto de todos los puntos, los cuales tienen distancias desde dos puntos fijos que al ser sumadas es igual a un valor constante. Los puntos fijos son denominados los focos de la elipse. Las elipses tienen dos ejes de simetrías. El eje con la mayor longitud es denominado el eje mayor y el eje con la menor longitud es denominado el eje menor. Los vértices de la elipse son los puntos finales del eje mayor y los covértices son los puntos finales del eje menor. El centro de una elipse es el punto de intersección del eje mayor y el eje menor. Los focos siempre están ubicados en el eje mayor.
A continuación, conoceremos la ecuación de la elipse que tiene un centro fuera del origen. Miraremos ecuaciones tanto para elipses orientadas verticalemente, como para elipses orientadas horizontalmente.
PRACÁLCULO
Relevante para…
Aprender sobre la ecuación de la elipse con centro fuera del origen.
- Forma estándar de elipses centradas fuera del origen
- Escribir la ecuación de elipses centradas fuera del origen usando los vértices y los focos
- Ejercicios resueltos de ecuación de la elipse con centro fuera del origen
- Ejercicios de ecuación de la elipse con centro fuera del origen para resolver
- Véase también
PRACÁLCULO
Relevante para…
Aprender sobre la ecuación de la elipse con centro fuera del origen.
Forma estándar de elipses centradas fuera del origen
Muchas veces, las elipses no están centradas en el origen, por lo que no podemos usar las ecuaciones más básicas que usamos cuando sí tenemos un centro en el origen. Sin embargo, similar a otras gráficas, las gráficas de las elipses pueden ser trasladadas horizontalmente y verticalmente.
Si es que una elipse es trasladada h unidades horizontalmente y k unidades verticalmente, su centro estará en (h, k). Podemos usar esta traslación en la ecuación estándar de una elipse reemplazando a x con $latex (x-h)$ y a y con $latex (y-k)$.
Además de tener elipses centradas en el origen y fuera del origen, también tenemos elipses que tienen una orientación vertical u horizontal.
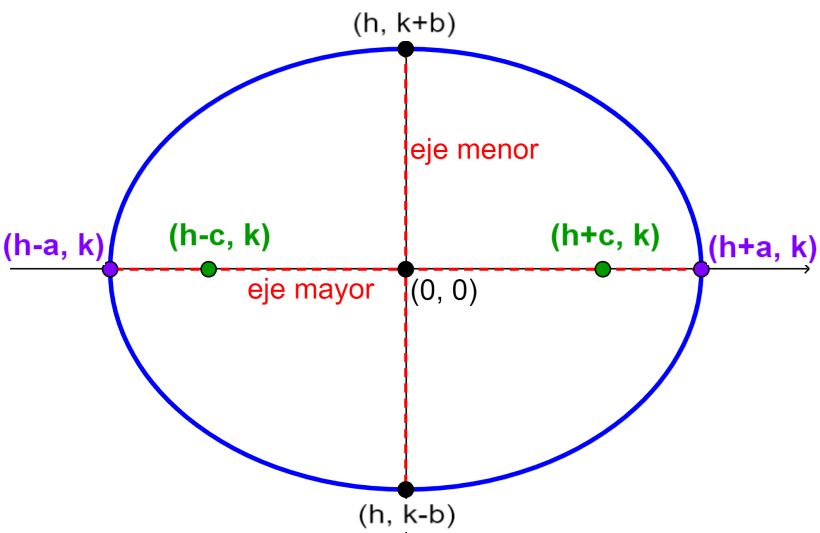
Ecuación de la elipse horizontal centrada fuera del origen
La forma estándar de una elipse con centro en (h, k), y con el eje mayor paralelo al eje x es:
| $latex \frac{{{(x-h)}^2}}{{{a}^2}}+\frac{{{(y-h)}^2}}{{{b}^2}}=1$ |
en donde,
- $latex a>b$
- El eje mayor mide $latex 2a$
- El eje menor mide $latex 2b$
- Los vértices están ubicados en $latex (h\pm a, k)$
- Los covértices están ubicados en $latex (h, k\pm b)$
- Los focos están ubicados en $latex (h \pm c, k)$, en donde, $latex {{c}^2}={{a}^2}-{{b}^2}$
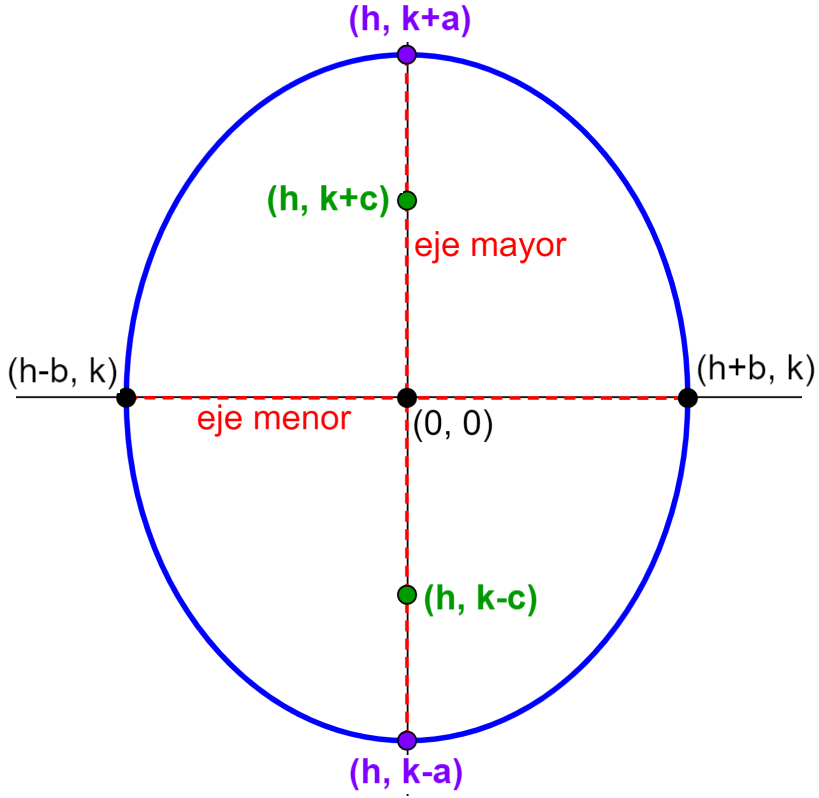
Ecuación de la elipse vertical centrada fuera del origen
La ecuación de una elipse en su forma estándar que tiene al centro en (h, k), y en la que su eje mayor es paralelo al eje y es:
| $latex \frac{{{(x-h)}^2}}{{{b}^2}}+\frac{{{(y-k)}^2}}{{{a}^2}}=1$ |
en donde,
- $latex a>b$
- La longitud del eje mayor es $latex 2a$
- La longitud del eje menor es $latex 2b$
- Los vértices están ubicados en $latex (h, k\pm a)$
- Los covértices están ubicados en $latex (h\pm b, k)$
- Los focos están ubicados en $latex (h, k\pm c)$, en donde, $latex {{c}^2}={{a}^2}-{{b}^2}$
Escribir la ecuación de elipses centradas fuera del origen usando los vértices y los focos
Usamos los siguientes pasos para determinar la ecuación de una elipse centrada fuera del origen si es que conocemos los vértices y los focos:
Paso 1: Determinamos si es que el eje mayor es paralelo al eje x o al eje y.
1.1. Si es que las coordenadas en y de los vértices son iguales a las coordenadas en y de los focos, el eje mayor es paralelo al eje x y usamos la ecuación $latex \frac{{{(x-h)}^2}}{{{a}^2}}+\frac{{{(y-k)}^2}}{{{b}^2}}=1$.
1.2. Si es que las coordenadas en x de los vértices son iguales a las coordenadas en y de los focos, el eje mayor es paralelo al eje y y usamos la ecuación $latex \frac{{{(x-h)}^2}}{{{b}^2}}+\frac{{{(y-k)}^2}}{{{a}^2}}=1$.
Paso 2: Podemos determinar las coordenadas del centro de la elipse (h, k) usando las coordenadas de los vértices y reconociendo que el centro se encuentra en el punto medio.
Paso 3: Encontramos el valor de $latex {{a}^2}$ al encontrar la longitud del eje mayor, 2a. Esta longitud es la distancia entre los dos vértices.
Paso 4: Encontramos el valor de $latex {{c}^2}$ usando los valores de h y k junto con las coordenadas de los focos.
Paso 5: Resolvemos para $latex {{b}^2}$ usando la ecuación $latex {{c}^2}={{a}^2}-{{b}^2}$.
Paso 6: Reemplazamos los valores de $latex {{a}^2}$, $latex {{b}^2}$, h y k en la ecuación obtenida en el paso 1.
Ejercicios resueltos de ecuación de la elipse con centro fuera del origen
Lo aprendido sobre las ecuaciones de elipses que tienen al centro en el punto (h, k) es aplicado para resolver los siguientes ejercicios. Analiza el proceso usado cuidadosamente.
EJERCICIO 1
Encuentra la ecuación de la elipse que tiene vértices en $latex (-1, -9)$ y $latex (-1, 3)$ y focos en $latex (-1, -8)$ y $latex (-1, 2)$.
Solución
Vemos que las coordenadas en x de los vértices y los focos son las mismas, por lo que el eje mayor es paralelo al eje y. Entonces, la ecuación de la elipse tendrá la siguiente forma:
$latex \frac{{{(x-h)}^2}}{{{b}^2}}+\frac{{{(y-k)}^2}}{{{a}^2}}=1$
Para encontrar el centro, usamos la fórmula del punto medio ya que el centro se encuentra entre los vértices $latex (-1, -9)$ y $latex (-1, 3)$. Entonces, tenemos:
$latex (h, k)=(\frac{-1+(-1)}{2}, \frac{-9+3}{2})$
$latex =(-1, -3)$
Ahora, vamos a encontrar $latex {{a}^2}$. La longitud del eje mayor, $latex 2a$, está limitada por los dos vértices. Entonces, la distancia entre los vértices es:
$latex 2a=3-(-9)$
$latex 2a=12$
$latex a=6$
Entonces, tenemos $latex {{a}^2}=36$.
Ahora, encontramos $latex {{c}^2}$. Para elipses verticales, los focos están dados por $latex (h, k\pm c)$. Entonces, tenemos $latex (h, k-c)=(-1,-8)$ y $latex (h, k+c)=(-1,2)$. Usamos el valor $latex k=-3$ en cualquiera de estos puntos y resolvemos:
$latex k+c=2$
$latex -3+c=2$
$latex c=5$
Entonces, tenemos $latex {{c}^2}=25$.
Ahora, usamos la ecuación $latex {{c}^2}={{a}^2}-{{b}^2}$ para obtener el valor de $latex {{b}^2}$. Entonces, tenemos:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex 25=36-{{b}^2}$
$latex {{b}^2}=11$
Finalmente, usamos los valores obtenidos en la ecuación de la elipse:
$latex \frac{{{(x+1)}^2}}{11}+\frac{{{(y+3)}^2}}{36}=1$
EJERCICIO 2
¿Cuál es la ecuación de la elipse que tiene vértices en $latex (-4, 2)$, $latex (8, 2)$ y focos en $latex (-2, 2)$, $latex (6, 2)$?
Solución
En este caso, las coordenadas en y de los vértices y los focos son las mismas. Esto significa que el eje mayor es paralelo al eje x. Por lo tanto, la ecuación de la elipse tendrá la siguiente forma:
$latex \frac{{{(x-h)}^2}}{{{a}^2}}+\frac{{{(y-k)}^2}}{{{b}^2}}=1$
Encontramos al centro usando la fórmula del punto medio, ya que el centro se encuentra entre los vértices $latex (-4, 2)$ y $latex (8, 2)$. Entonces, tenemos:
$latex (h, k)=(\frac{-4+8}{2}, \frac{2+2}{2})$
$latex =(2, 2)$
Encontramos $latex {{a}^2}$ usando la longitud del eje mayor, $latex 2a$. Esta longitud es igual a la distancia entre los vértices. Entonces, tenemos:
$latex 2a=8-(4)$
$latex 2a=12$
$latex a=6$
Entonces, tenemos $latex {{a}^2}=36$.
Vamos a encontrar $latex {{c}^2}$. En una elipse horizontal, los focos están dados por $latex (h\pm c, k)$. Entonces, tenemos $latex (h-c, k)=(-2, 2)$ y $latex (h+c, k)=(6,2)$. Usamos cualquiera de estos puntos con el valor $latex h=2$ y resolvemos:
$latex h+c=6$
$latex 2+c=6$
$latex c=4$
Entonces, tenemos $latex {{c}^2}=16$.
Encontramos el valor de $latex {{b}^2}$ usando la ecuación $latex {{c}^2}={{a}^2}-{{b}^2}$. Entonces, tenemos:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex 16=36-{{b}^2}$
$latex {{b}^2}=20$
Finalmente, usamos los valores obtenidos en la ecuación de la elipse:
$latex \frac{{{(x-2)}^2}}{36}+\frac{{{(y-2)}^2}}{20}=1$
Ejercicios de ecuación de la elipse con centro fuera del origen para resolver
Usa lo aprendido sobre las ecuaciones de elipses con centro fuera del origen para resolver los siguientes ejercicios. Mira los ejercicios resueltos de arriba en caso de necesitar ayuda con esto.
Véase también
¿Interesado en aprender más sobre elipses? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
