Las gráficas de funciones pueden ser usadas para determinar el dominio y el rango. Las gráficas nos dan una idea de cuáles valores de x y cuáles valores de y están siendo tomados. Muchas veces esto puede ser suficiente para determinar totalmente el dominio y el rango. Sin embargo, habrá ocasiones en las que tendremos que usar álgebra para comprobar o ser más específicos.
A continuación, aprenderemos cómo determinar el dominio y rango de una gráfica de una función. Veremos varios ejemplos para ilustrar estas ideas.
¿Cómo encontrar el dominio y el rango?
Dominio
Recordamos que el dominio de una función es el conjunto de todos los valores posibles de la variable independiente. Es decir, el dominio es el conjunto de todos los valores de x que resultarán en valores reales de y.
Para encontrar el dominio, debemos recordar que:
- El denominador de una fracción no puede ser igual a cero.
- El número debajo de una raíz cuadrada no puede ser un número negativo.
Determinamos el dominio al encontrar todos los valores de la variable independiente que sí podemos usar y excluir los valores que no resultan en salidas reales de la función.
Rango
Recordamos que el rango de una función es el conjunto de todos los valores posibles de la variable dependiente. Es decir, el rango es el conjunto de todos los valores de y que resultan al usar el dominio como entrada.
El rango puede ser determinado al encontrar los valores máximos o mínimos de y. También, podemos sustituir diferentes valores de x y analizar qué tipo de valores de y obtenemos. Las gráficas son particularmente útiles para determinar el rango.
Ejemplos de dominio y rango de una gráfica
EJEMPLO 1
Encuentra el dominio y el rango de la función f que tiene la siguiente gráfica:
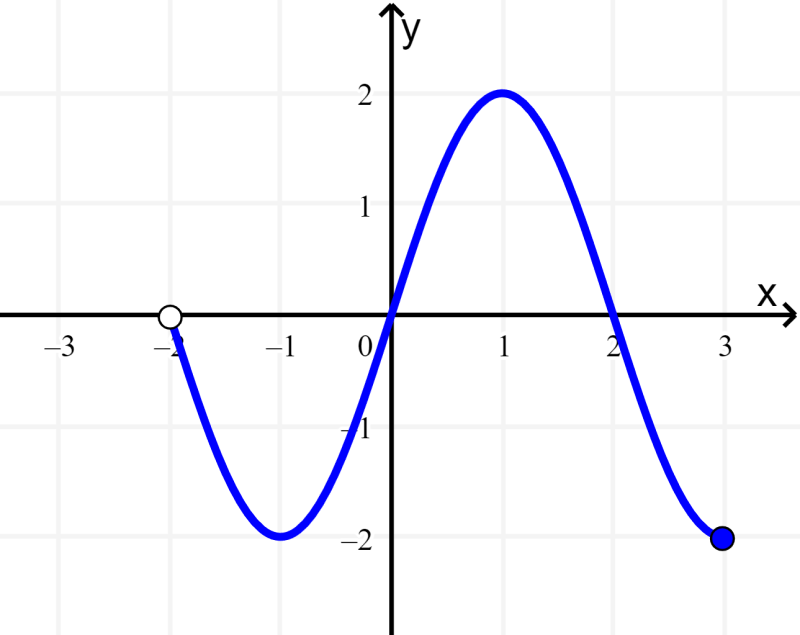
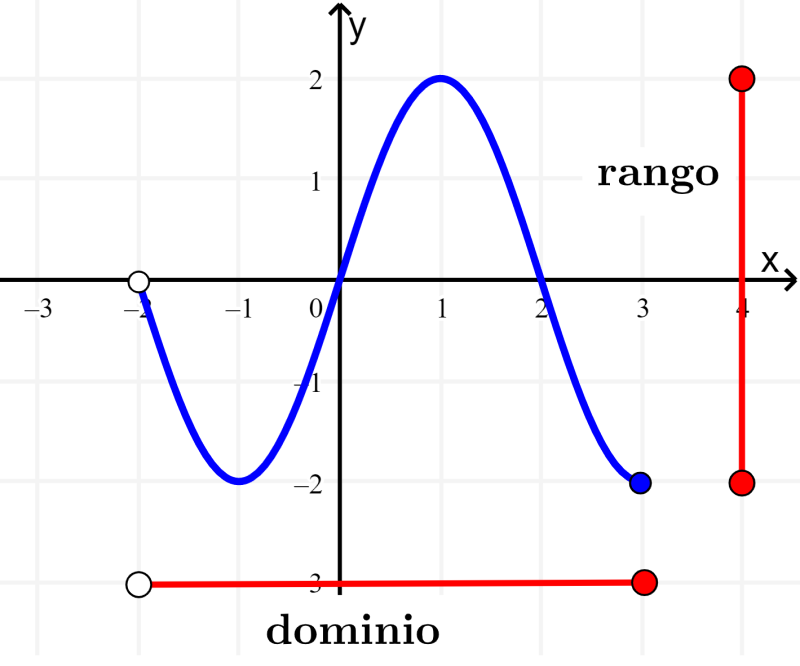
Solución: Podemos ver que la gráfica se extiende horizontalmente desde -2 hasta 3, pero el -2 no está incluido. Entonces, el dominio es (-2, 3].
También, vemos que la gráfica se extiende verticalmente desde 2 hasta -2, por lo que el rango es [-2, 2].
EJEMPLO 2
La siguiente gráfica representa a la función $latex f(x)=\frac{1}{x+5}$. Determina su rango y dominio.
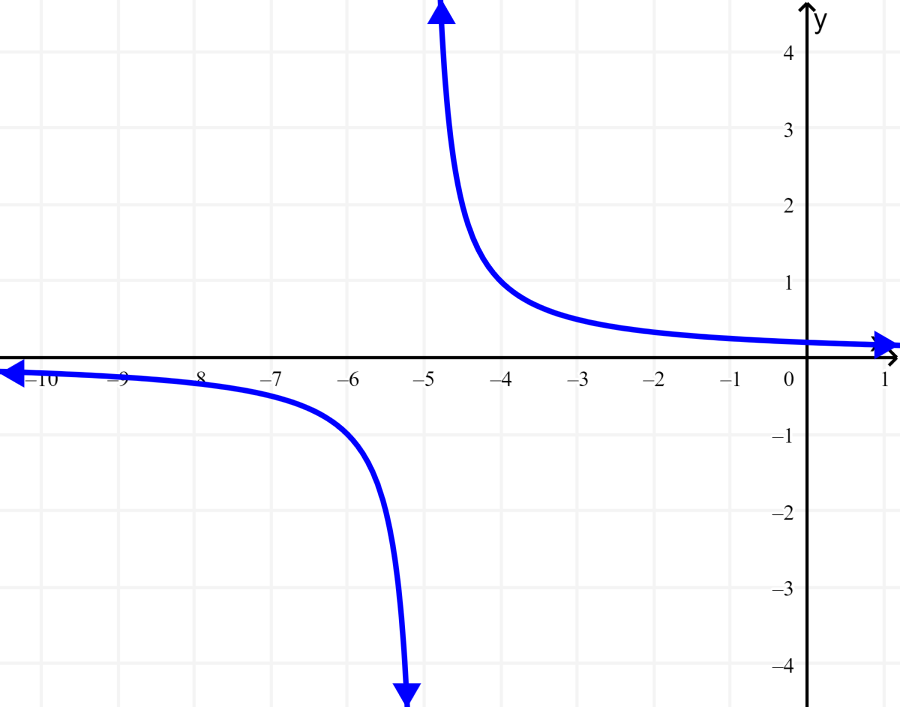
Solución: Podemos ver que la gráfica se extiende horizontalmente más allá de lo que podemos ver en la gráfica, por lo que podemos asumir que se extiende desde infinito negativo hasta infinito positivo.
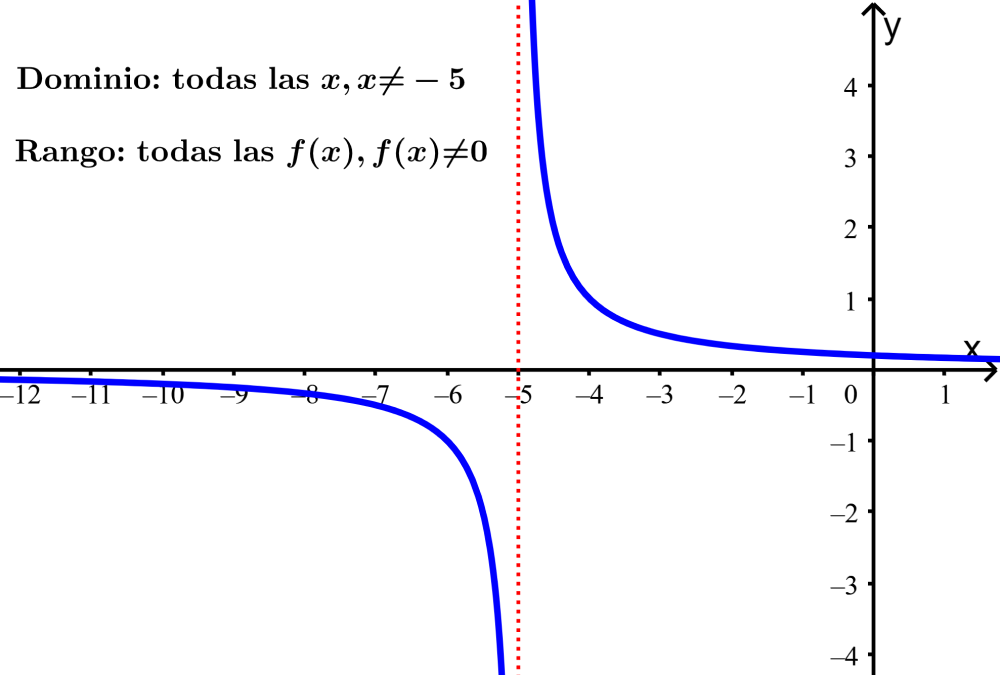
Sin embargo, podemos ver que la gráfica nunca tiene un valor de -5 en x, por lo que tenemos que excluir este valor del dominio. Entonces, el dominio es todos los números reales de x y $latex x\neq -5$.
De igual forma, vemos que la gráfica se extiende verticalmente más allá de lo que podemos ver en la gráfica, por lo que decimos que se extiende desde infinito negativo hasta infinito positivo.
Aquí, vemos que los valores de y nunca alcanzan el valor de cero, por lo que lo excluimos del rango. Entonces, el rango es todos los valores reales de $latex f(x)$ y $latex f(x\neq 0)$.
EJEMPLO 3
La siguiente gráfica representa a la función $latex f(x)={{x}^2}+5$. Determina su rango y dominio.
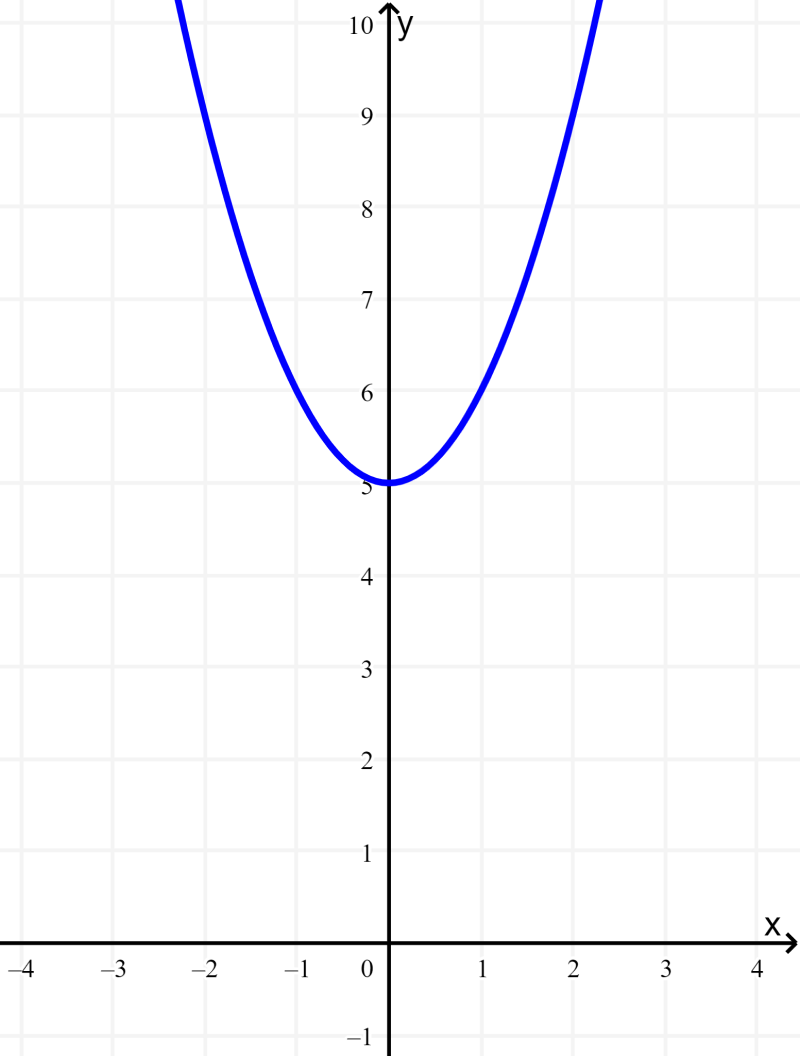
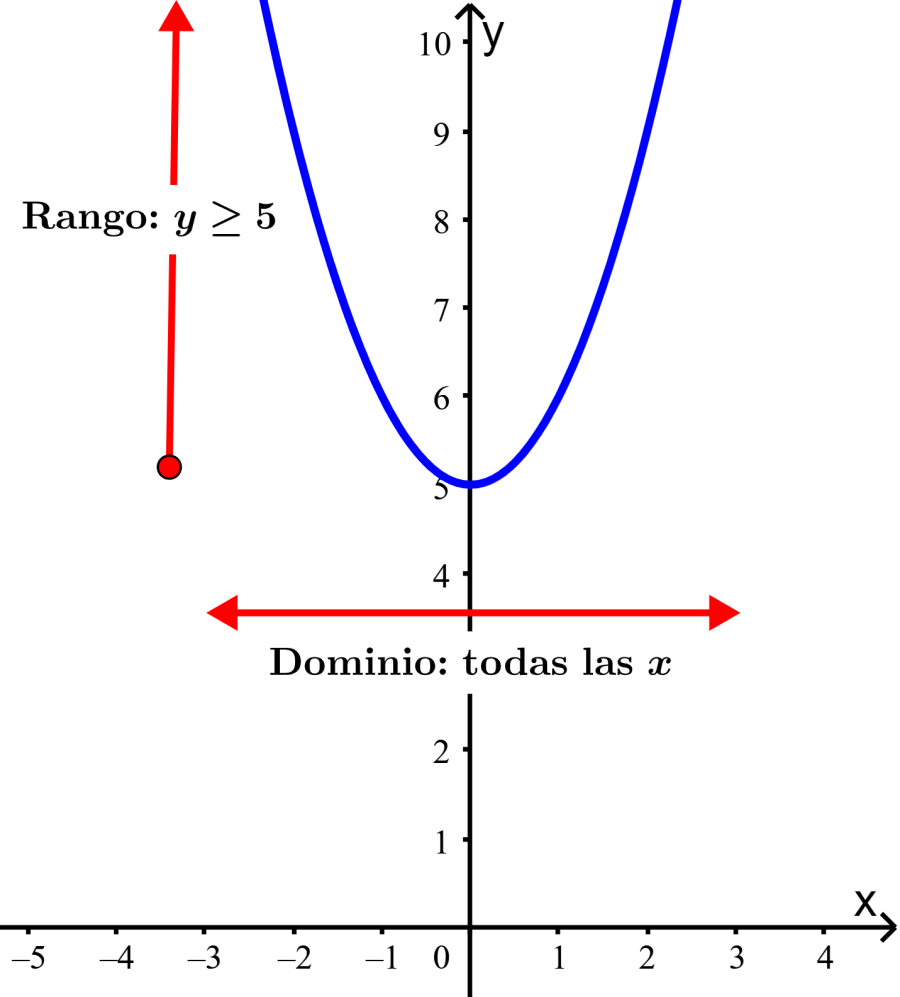
Solución: Esta es una gráfica cuadrática, por lo se extiende horizontalmente desde infinito negativo hasta infinito positivo. Eso significa que el dominio es todos los números reales de x.
También vemos que la gráfica se extiende verticalmente desde 5 hasta infinito positivo. Entonces, el rango es todos los números reales de y y $latex y\geq 5$.
EJEMPLO 4
La siguiente es la gráfica de la función $latex \sqrt{-t+2}$. ¿Cuál es su dominio y su rango?
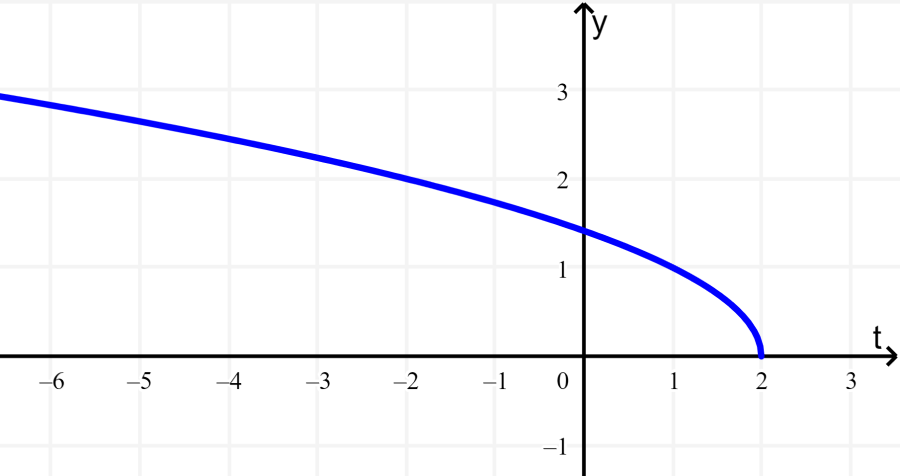
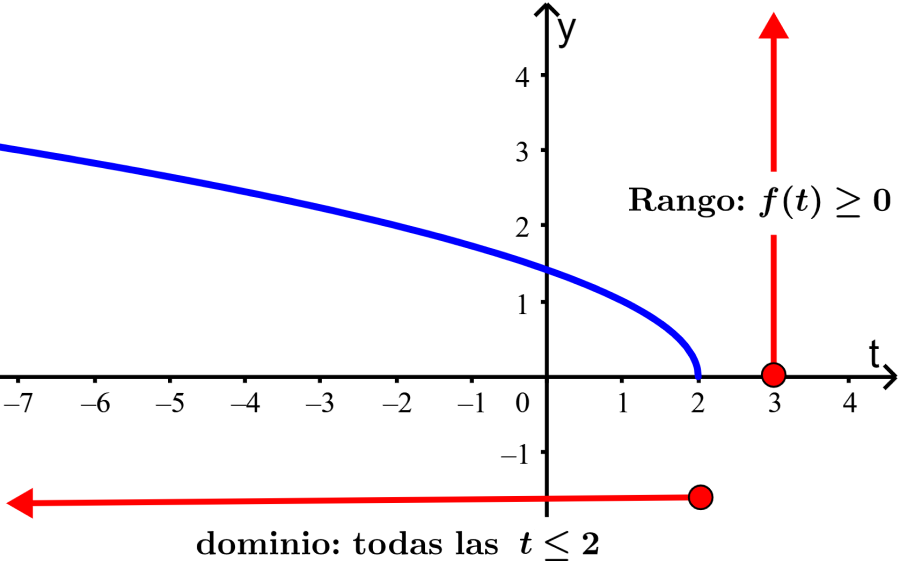
Solución: Vemos que la función se extiende indefinidamente hacia la izquierda y toma valores hasta 2. Entonces, su dominio es todos los números reales de t, en donde $latex t\leq 2$.
En el caso del rango, vemos que la función solo toma valores positivos y se extiende indefinidamente hacia arriba. Entonces, el rango es todos los números reales de $latex f(t)$ y $latex f(t)\geq 0$.
EJEMPLO 5
Encuentra el dominio y el rango de la siguiente función:
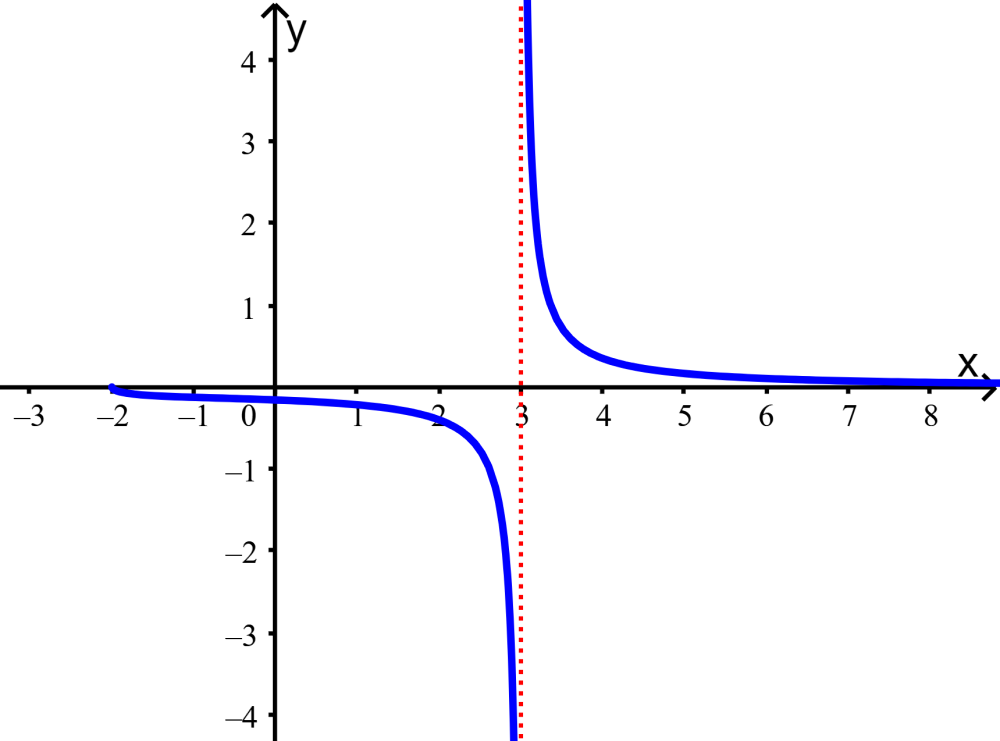
Solución: Podemos ver que esta función tiene valores horizontales que empiezan en $latex x=-2$ y se extienden indefinidamente hacia la derecha. Sin embargo, vemos que la función tiene una asíntota en $latex x=3$, es decir, la función nunca toma ese valor.
Por lo tanto, el dominio de la función es todos los números reales de x, en donde $latex x\geq -2$ y $latex x\neq 3$.
En el caso del rango, vemos que la gráfica se extiende desde infinito negativo hasta infinito positivo. También vemos que, a pesar de que pareciera que la gráfica nunca resulta en $latex y=0$, podemos ver que la función toma este valor en el punto $latex x=-2$.
Entonces, el rango de la función es todos los números reales de y.
Véase también
¿Interesado en aprender más sobre gráficas de funciones y dominio y rango? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
