Todas las funciones trigonométricas son básicamente las proporciones trigonométricas de cualquier ángulo dado. Por ejemplo, si es que tomamos a las funciones $latex f(x)=\sin(x)$, $latex f(x)=\tan(x)$, etc., estamos considerando a estas proporciones trigonométricas como funciones. El dominio y el rango de estas funciones trigonométricas dependerá en la naturaleza de sus proporciones trigonométricas correspondientes.
A continuación, conoceremos el dominio y el rango de las funciones trigonométricas fundamentales como seno, coseno y tangente. También, veremos el dominio y el radio de las funciones cosecante, secante y tangente.
ÁLGEBRA
Relevante para…
Aprender sobre el dominio y el rango de funciones trigonométricas.
ÁLGEBRA
Relevante para…
Aprender sobre el dominio y el rango de funciones trigonométricas.
Dominio y rango de funciones trigonométricas (sin, cos, tan)
Seno
Podemos empezar considerando a la identidad trigonométrica más simple:
$latex {{\sin}^2}(x)+{{\cos}^2}(x)=1$
De esta identidad, podemos derivar las siguientes interpretaciones:
$latex {{\cos}^2}(x)=1-{{\sin}^2}(x)$
$latex \cos(x)=\sqrt{1-\sin^2(x)}$
Sabemos que la función coseno está definida para valores reales, por lo que el valor dentro de la raíz cuadrada no puede ser negativo. Entonces, podemos formar la desigualdad:
$latex 1-\sin^2(x)\geq 0$
$latex \sin^2(x)\leq 1$
$latex \sin(x)\in [-1, 1]$
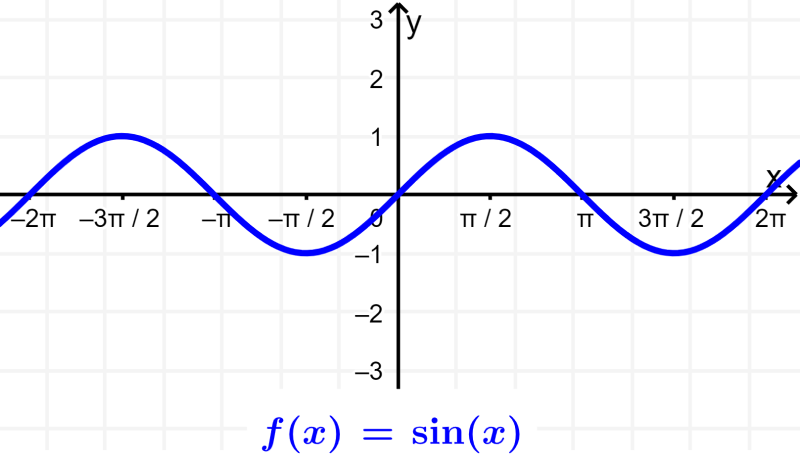
Entonces, ya hemos obtenido el dominio y el rango para la función seno. El dominio es todos los números reales de x ya que no tenemos ninguna restricción en los valores de x. El rango es desde -1 hasta 1, incluyendo a estos valores. Podemos comprobar esto mirando su gráfica:
Coseno
De igual forma, usando la misma metodología, tenemos:
$latex 1-\cos^2(x)\geq 0$
$latex \cos^2(x)\leq 1$
$latex \cos(x)\in [-1, 1]$
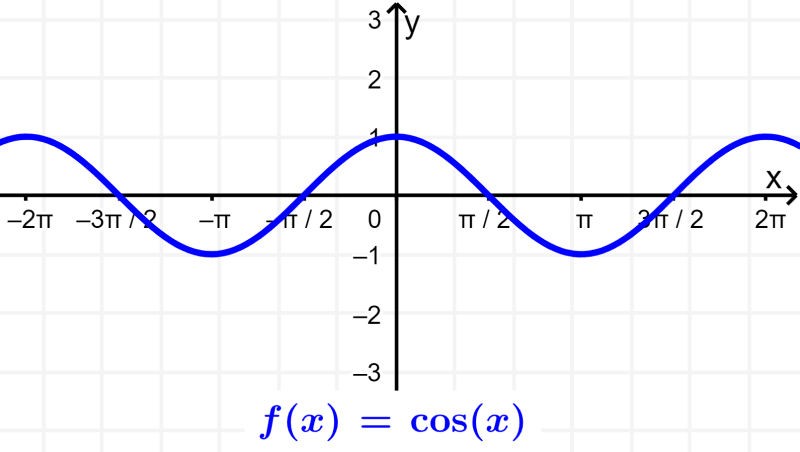
Entonces, el dominio de la función coseno también es todos los números reales de x. El rango de la función coseno es desde -1 hasta 1, incluyendo a estos valores. Podemos verificar esto mirando su gráfica:
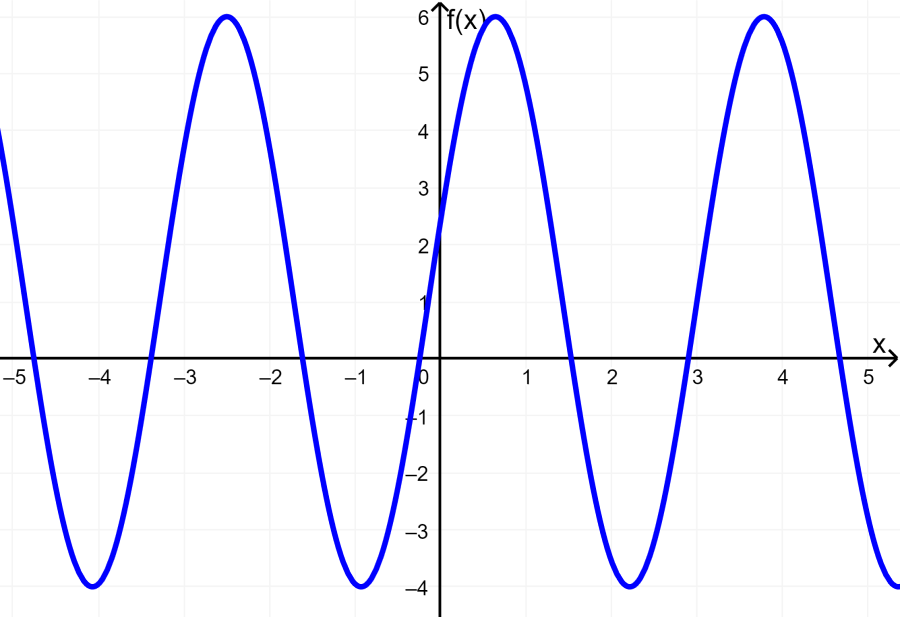
Algo importante que debemos tener en cuenta es que el rango de seno y coseno depende de la amplitud de las funciones. Por ejemplo, si tenemos $latex f(x)=5\cos(x)$, el rango es desde -5 a 5.
Tangente
Ahora, miremos la función $latex f(x)=\tan(x)$. Sabemos que $latex \tan(x)=\frac{\sin(x)}{\cos(x)}$. Esto significa que la función tangente está definida para todos los valores a excepción de aquellos que hacen que $latex \cos(x)$ sea igual a cero, ya que una fracción con denominador igual a cero es indefinida.
Ahora, sabemos que $latex \cos(x)$ es cero para los ángulos $latex \frac{\pi}{2},~\frac{3\pi}{2}, ~\frac{5\pi}{2}$, etc.
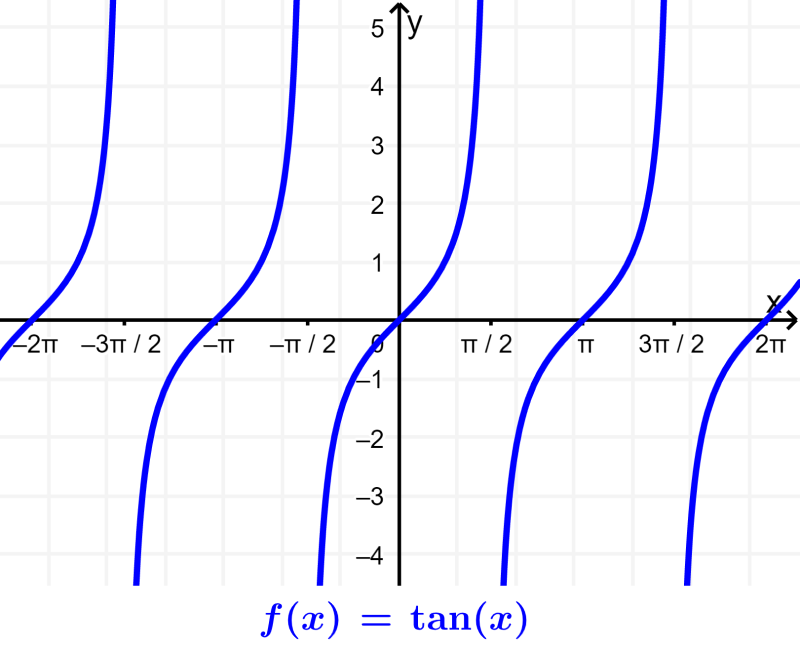
Por lo tanto, el dominio de la función tangente es $latex R-\frac{(2n+1)\pi}{2}$ y el rango es todos los números reales. Podemos ver esto en la gráfica:
Dominio y rango de las funciones cosec, sec y cot
Secante
Sabemos que la secante es la función recíproca del coseno. Entonces, tenemos:
$latex \sec(x)=\frac{1}{\cos(x)}$
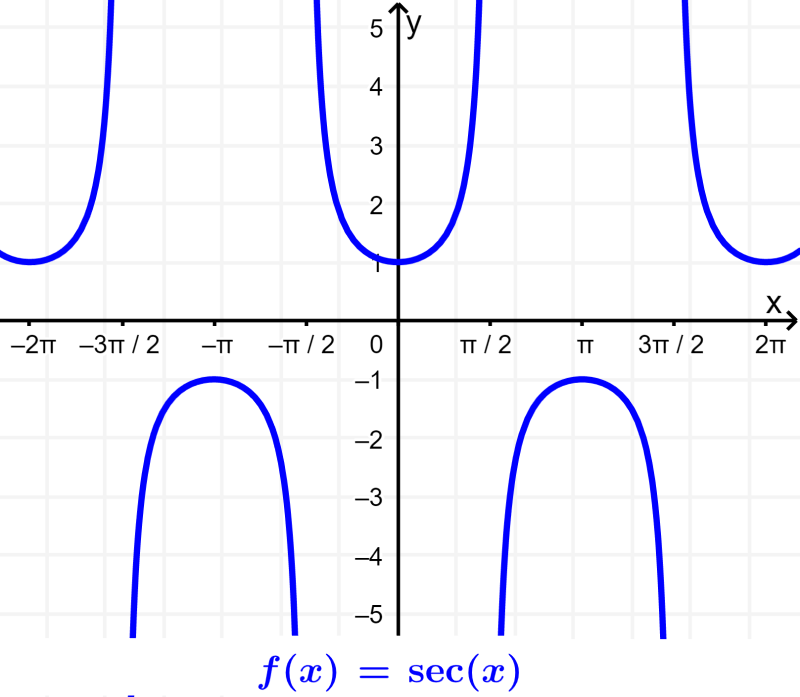
Eso significa que la secante no estará definida para los puntos en donde $latex \cos(x)=0$. Entonces, el dominio de $latex f(x)=\sec(x)$ será $latex R-\frac{(2n+1)\pi}{2}$.
El rango de la secante será $latex R-(-1, 1)$. Dado que $latex \cos(x)$ se ubica entre -1 hasta 1, la secante nunca puede estar en esta región. Podemos mirar su gráfica:
Cosecante
La cosecante es la función recíproca del seno. Entonces, tenemos:
$latex \csc(x)=\frac{1}{\sin(x)}$
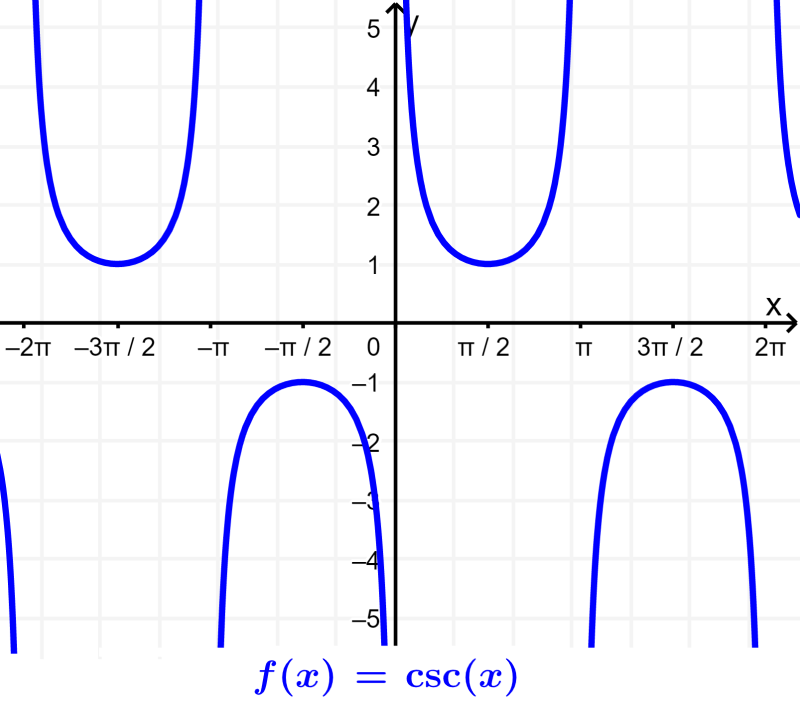
Sabemos que la cosecante no estará definida para los puntos en donde $latex \sin(x)=0$. Por lo tanto, el dominio de $latex f(x)=\csc(x)$ será $latex R-n\pi$.
El rango de la cosecante será $latex R-(-1, 1)$. Esto se debe a que $latex \sin(x)$ se ubica entre -1 hasta 1, por lo que la cosecante nunca puede estar en esta región. Podemos comprobarlo con su gráfica:
Cotangente
La cotangente es la función recíproca de la tangente. Entonces, tenemos:
$latex \cot(x)=\frac{1}{\tan(x)}$
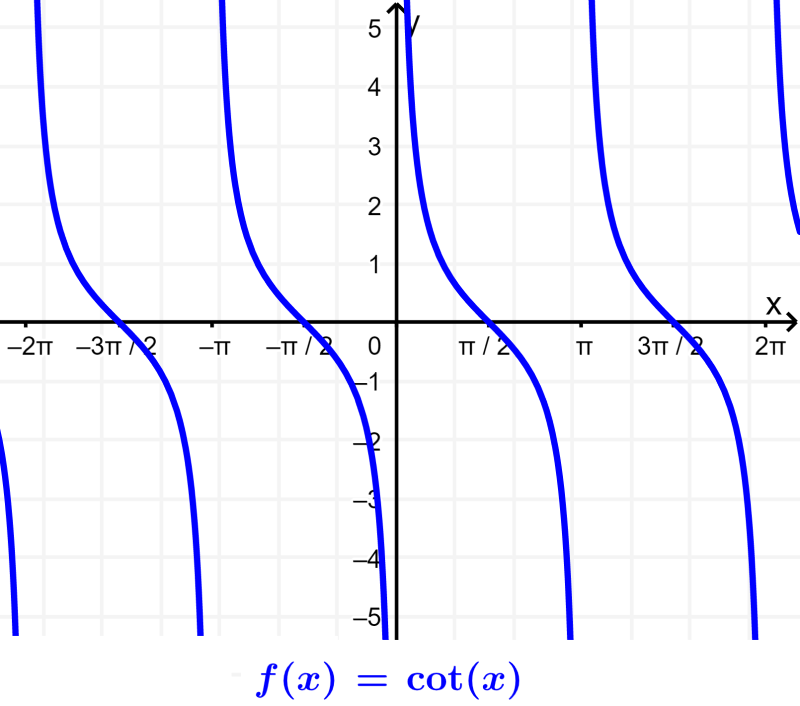
La función cotangente no estará definida para los puntos en donde $latex \tan(x)=0$. Entonces, el dominio de $latex f(x)=\cot(x)$ será $latex R-n\pi$.
El rango de la cotangente será $latex R-(-1, 1)$ el conjunto de todos los números reales porque no tenemos ninguna restricción. Podemos mirar su gráfica:
Véase también
¿Interesado en aprender más sobre funciones trigonométricas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
