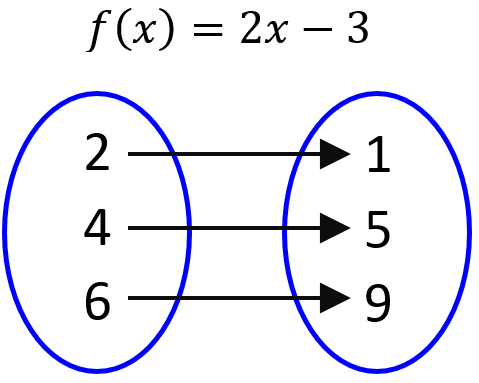En este artículo, aprenderemos a encontrar el dominio y el rango de una función racional o bien usando su gráfica o usando reglas algebraicas definidas. Empezaremos haciendo una breve revisión de lo que significan el dominio y el rango.
Luego, veremos los métodos usados para encontrar al dominio y al rango de funciones racionales. Finalmente, veremos algunos ejemplos resueltos que ilustran el uso de estos métodos.
¿Qué es el dominio y el rango de funciones?
Si es que pensamos en una función como un mapeo que relaciona a una entrada con una salida, el dominio sería el conjunto de entradas y el rango el conjunto de salidas. Consideremos el siguiente diagrama de mapeo:
Podemos ver a las entradas en la izquierda y las salidas en la derecha. Aquí, el dominio es el conjunto {2, 4, 6} y el rango es el conjunto {1, 5, 9}. Si es que consideramos a la función $latex f(x)=2x-3$ con el dominio {1, 2, 3, 4}, podemos encontrar el rango al sustituir cada uno de los valores del dominio en la función:
$latex f(1)=2(1)-3=-1$
$latex f(2)=2(2)-3=1$
$latex f(3)=2(3)-3=3$
$latex f(4)=2(4)-3=9$
Entonces, el rango es el conjunto {-1, 1, 3, 9}.
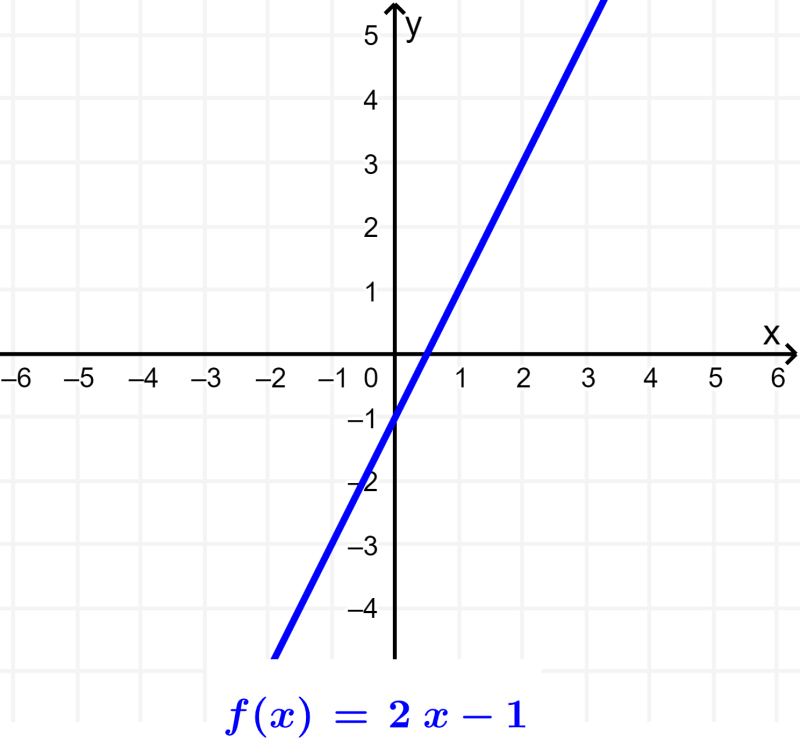
Ahora, consideremos a la función $latex f(x)=2x-1$ con dominio $latex x\in R$ (significa que x pertenece al conjunto de todos los números reales). Puede resultar útil mirar su gráfica para facilitar la determinación del rango:
Podemos ver que la gráfica es una línea recta y cada entrada real tiene una salida real, y dado que la línea continúa hacia el infinito positivo y negativo, cualquier número real de salida es posible. Entonces, el rango es todos los números reales.
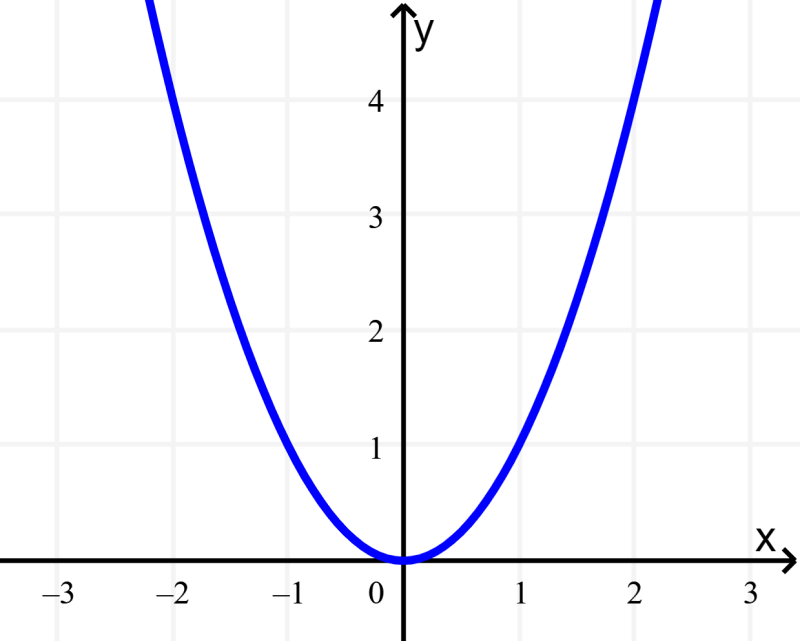
Si es que ahora miramos a la función cuadrática $latex f(x)={{x}^2}$, la cual tiene un dominio que es todos los números reales, podemos mirar a su gráfica para determinar el rango:
Vemos que para cada entrada, la salida siempre es positiva. Entonces, el rango de la función es igual a todos los números reales mayores o iguales que cero.
Dominio y rango de funciones racionales
Generalmente, tendemos a definir al dominio y al rango de funciones sobre los números reales, por lo que haremos lo mismo aquí.
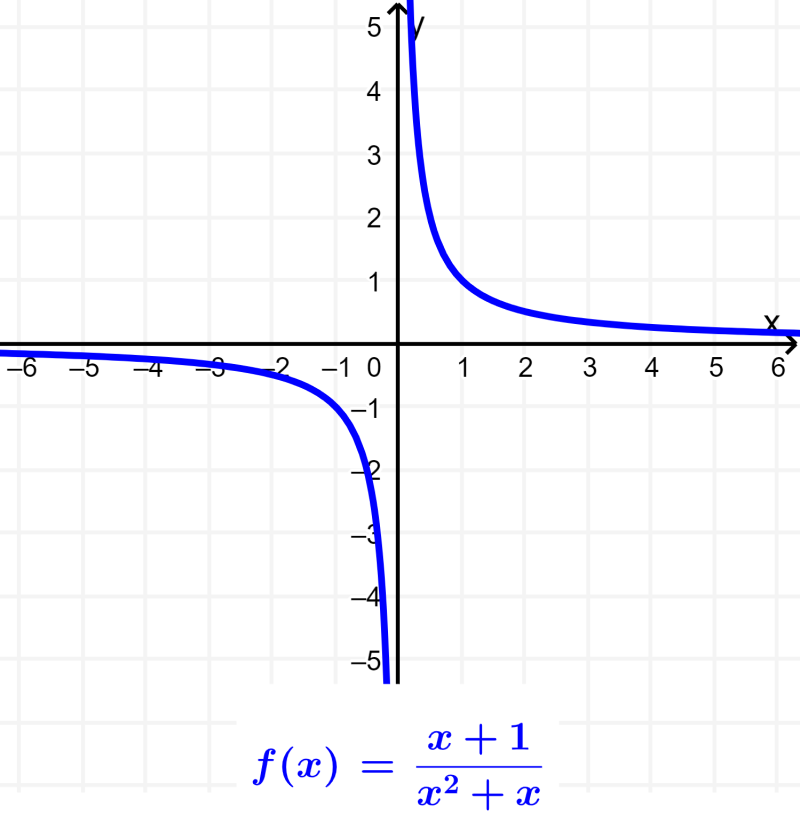
Sin embargo, usaremos estrategias diferentes para encontrar el dominio y rango de funciones racionales, ya que obtener las gráficas de estas funciones no es muy fácil. Consideremos a la siguiente función racional:
$latex f(x)=\frac{3}{x+2}$
Observamos que, para una entrada de -2, obtenemos una salida de $latex \frac{3}{0}$.
Sabemos que la división por cero es indefinida, por lo que la función está indefinida en este punto. Sin embargo, cualquier otra entrada tendrá una salida en números reales, por lo que concluimos que el dominio es todos los números reales excluyendo al -2. Podemos escribir a esto como:
$latex R- \{-2\}$
Al considerar la naturaleza de la función, podemos ver que cualquier número real de salida puede ser logrado con la excepción del cero. Esto se debe a que, a medida que x se vuelve más grande en magnitud, la salida se hace más pequeña, pero la salida nunca puede ser igual a cero.
Entonces, el rango de la función es:
$latex R-\{0\}$
En general, podemos calcular el dominio de una función racional al identificar cualquier punto en donde la función no está definida. Esto significa encontrar cualquier punto que haga que el denominador sea igual a cero.
Para encontrar el rango de una función racional, podemos identificar cualquier punto que no puede ser alcanzado con ninguna entrada. Esto es generalmente encontrado al considerar los límites de la función a medida que la magnitud de las entradas se hace más grande.
Dominio y rango de funciones racionales con ejemplos
Los siguientes ejemplos ilustran los conceptos detallados anteriormente.
EJEMPLO 1
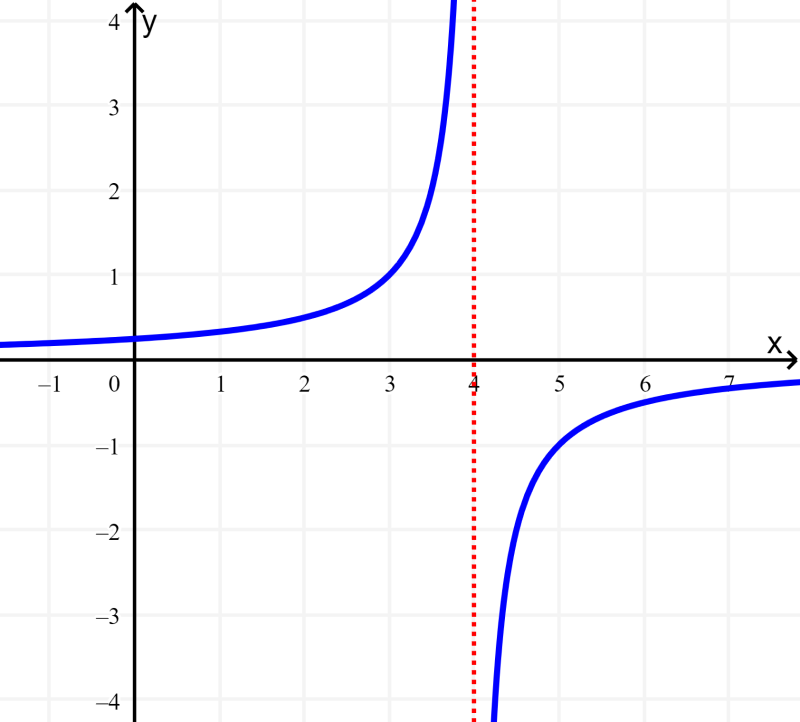
Encuentra el dominio y el rango de la función $latex f(x)= -\frac{1}{x-4}$.
Solución: Mirando a la gráfica, pareciera que el dominio es $latex R-\{4\}$ y el rango es $latex R-\{0\}$. Sin embargo, vamos a comprobar esto algebraicamente.
Sabemos que una función no está definida para entradas que resultan en denominadores iguales a cero. Podemos formar una ecuación con el denominador para encontrar el punto indefinido:
$latex x-4=0$
$latex x=4$
Esto confirma que el dominio es $latex R-\{4\}$. Para confirmar el rango, tenemos que identificar los valores que no pueden ser alcanzados con el dominio dado. A medida que x se hace más grande, la salida tiende a cero, pero nunca llega a ser cero. Entonces, el rango es $latex R-\{0\}$.
EJEMPLO 2
Encuentra el dominio y el rango de la función $latex f(x)= \frac{1}{x-10}$.
Solución: En este caso no tenemos una gráfica, por lo que tenemos que resolver el problema algebraicamente.
Nuevamente, sabemos que la expresión $latex \frac{1}{0}$ no está definida, por lo que formamos una ecuación con el denominador para encontrar el punto indefinido:
$latex x-10=0$
$latex x=10$
Entonces, sabemos que el dominio de la función es $latex R-\{10\}$. Para identificar el rango, tenemos que identificar los valores que no pueden ser alcanzados con el dominio dado.
A medida que x se hace más grande, la salida tiende a cero, pero nunca llega a ser cero. Entonces, el rango es $latex R-\{0\}$.
EJEMPLO 3
Encuentra el dominio de la función $latex f(x)= \frac{3}{x-3}+\frac{1}{x+4}$.
Solución: Sabemos que las funciones racionales solo están definidas cuando su denominador es diferente de cero. En esta función, podemos ver que hay dos puntos para los que no está definida: cuando $latex x-3=0$ y $latex x+4=0$.
Esto significa que la función no está definida cuando $latex x=-4$ y $latex x=3$. Entonces, el dominio de la función es todos los números reales a excepción del -4 y el 3, denotado como $latex R-\{-4, 3\}$.
Si es que quisieramos encontrar el rango de esta función, a pesar de que cada una de las expresiones racionales no puede tomar un valor de cero, sí existe una entrada de x que resulta en cero, la cual es $latex x=-\frac{9}{4}$. Entonces, el rango de la función es todos los números reales $latex (R)$.
EJEMPLO 4
Determina el dominio de la función $latex f(x)= \frac{{{x}^2}+5}{5{{x}^3}+50x}$.
Solución: Recordamos que las funciones racionales solo están definidas cuando su denominador es diferente de cero. Entonces, para encontrar el dominio de la función, tenemos que encontrar los ceros de la ecuación en el denominador:
$latex 5{{x}^3}+50x=0$
Podemos factorizar la x:
$latex x(5{{x}^2}+50)=0$
Podemos ver que tenemos un cero cuando $latex x=0$. Sin embargo, la cuadrática $latex 5{{x}^2}+50$ no tiene raíces reales. Por lo tanto, el único cero del denominador es $latex x=0$. El dominio es todos los números relaes a excepción del cero, denotado como $latex R-\{0\}$.
Véase también
¿Interesado en aprender más sobre funciones racionales? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
