Las funciones logarítmicas son las funciones inversas de las funciones exponenciales. Esto significa que su dominio y su rango se intercambian. El dominio de las funciones logarítmicas es igual a todos los números reales mayores o menores que la asíntota vertical. El rango de las funciones exponenciales siempre es igual a todos los números reales, ya que no tenemos restricciones con los valores de salida.
A continuación, aprenderemos cómo determinar el dominio y el rango de funciones logarítmicas. Además, veremos algunos ejemplos con las gráficas de las funciones para ilustrar estas ideas.
ÁLGEBRA
Relevante para…
Aprender sobre el dominio y el rango de funciones logarítmicas.
ÁLGEBRA
Relevante para…
Aprender sobre el dominio y el rango de funciones logarítmicas.
¿Cómo encontrar el dominio y el rango de funciones logarítmicas?
Los límites en el dominio de las funciones logarítmicas resultan del hecho que es imposible tomar el logaritmo de un número negativo. Por otra parte, las funciones logarítmicas no tienen límites en el rango.
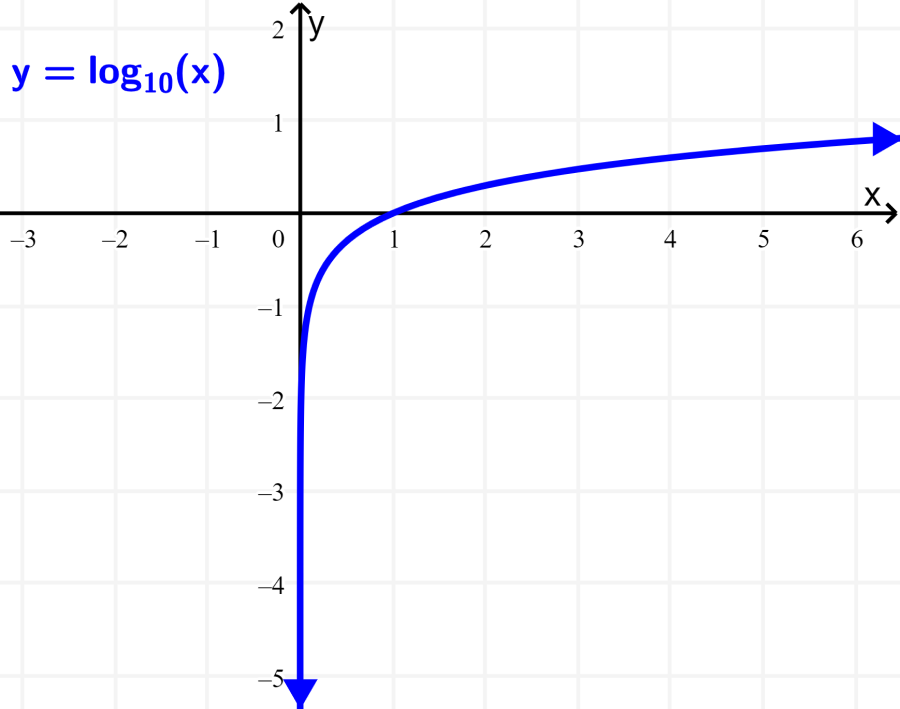
Podemos mirar la gráfica de la función logarítmica “estándar” $latex f(x)=\log(x)$:
Vemos que la gráfica de la función $latex f(x)=\log(x)$ tiene un punto clave en (1, 0). Desde este punto, la gráfica tiene una asíntota en la izquierda que se acerca a $latex x=0$. Además, desde el punto (1, 0), la gráfica asciende gradualmente hacia la derecha con ningún límite superior.
Visualizando a la gráfica, fácilmente podemos determinar el dominio y el rango. Recordemos que el dominio es el conjunto de todos los valores que la variable independiente puede tomar.
Entonces, el dominio de la función logarítmica “estándar” es todos los números mayores que 0 hasta infinito positivo:
El dominio es $latex 0<x<+\infty $
Recordemos que el rango es el conjunto de todos los valores que la variable dependiente puede tomar. En la gráfica, vemos que en la parte izquierda la función se va hacia infinito negativo.
En la parte derecha, vemos que la función asciende gradualmente y se va hacia infinito positivo. Entonces, el rango es igual a todos los números reales desde infinito negativo hasta infinito positivo:
El rango es $latex -\infty<y<+\infty $
Ahora, podemos determinar el rango y el dominio de otras funciones logarítmicas al considerar la manera en la que la función y la gráfica cambian a medida que introducimos varias constantes. Podemos usar las siguientes constantes:
$latex y=a~\log(x-h)+k$
Usando estas constantes, el punto (1, 0) cambia a $latex (h, k)$. La h representa a la traslación horizontal y la k representa a la traslación vertical. Lo importante aquí es que la asíntota cambia con el valor de h y esto cambia al dominio.
Sin embargo, el rango no es afectado y sigue siendo todos los números reales.
Ejemplos de dominio y rango de funciones logarítmicas
EJEMPLO 1
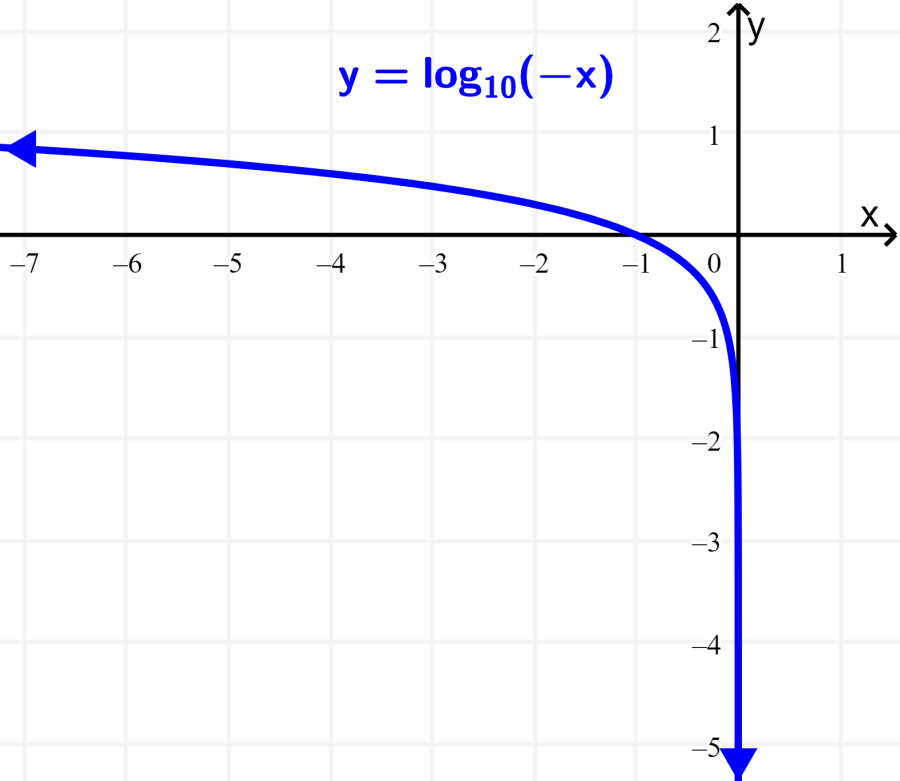
¿Cuál es el dominio y el rango de la función $latex f(x)=\log(-x)$?
Solución: Este cambio en la función, produce una reflexión con respecto al eje y. Debido a esta reflexión, el punto clave será (-1, 0). Desde allí, la función se acercará a la asíntota hacia abajo en la parte derecha y se acercará a $latex x=0$.
Desde el punto clave, la función ascenderá gradualmente hacia infinito en la parte izquierda. Entonces, el dominio es desde negativo infinito hasta 0:
Dominio: $latex -\infty<x<0$
El rango sigue siendo todos los números reales:
Rango: $latex -\infty<y<\infty$
Usando notación de intervalos, tenemos:
Dominio: $latex (-\infty, 0)$
Rango: $latex (-\infty, \infty)$
Podemos verificar esto en la gráfica de la función:
EJEMPLO 2
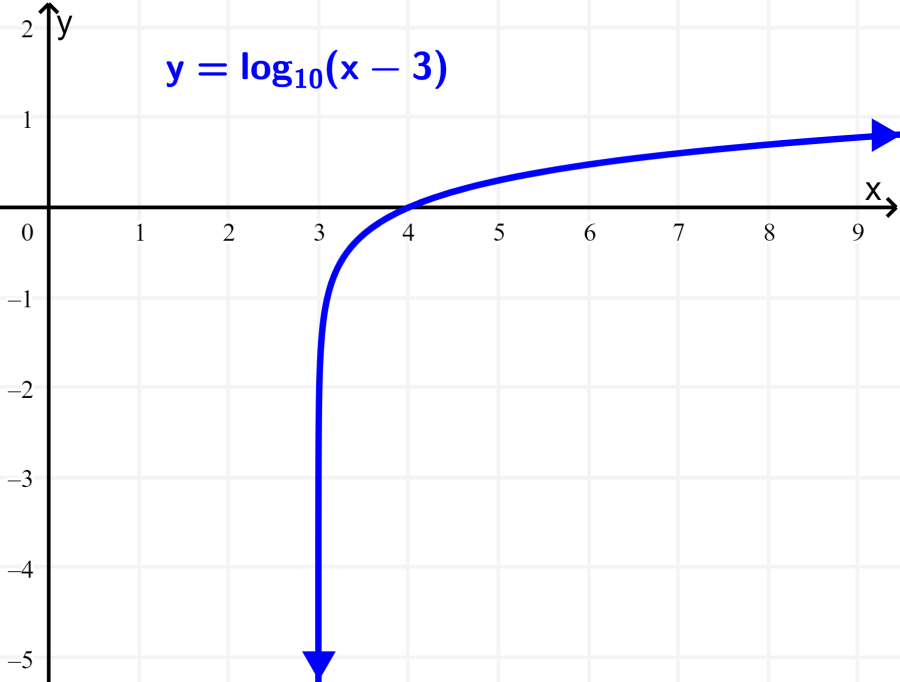
Encuentra el dominio y el rango de $latex f(x)=\log(x-3)$.
Solución: El valor de h de 3 hace que la función “estándar” y su asíntota se muevan hacia la derecha por 3 unidades. Esto cambia el dominio de la función. Entonces, el dominio es:
Dominio: $latex 3<x<\infty$
El rango de la función nunca cambia por lo que sigue siendo:
Rango: $latex -\infty<x<\infty$
EJEMPLO 3
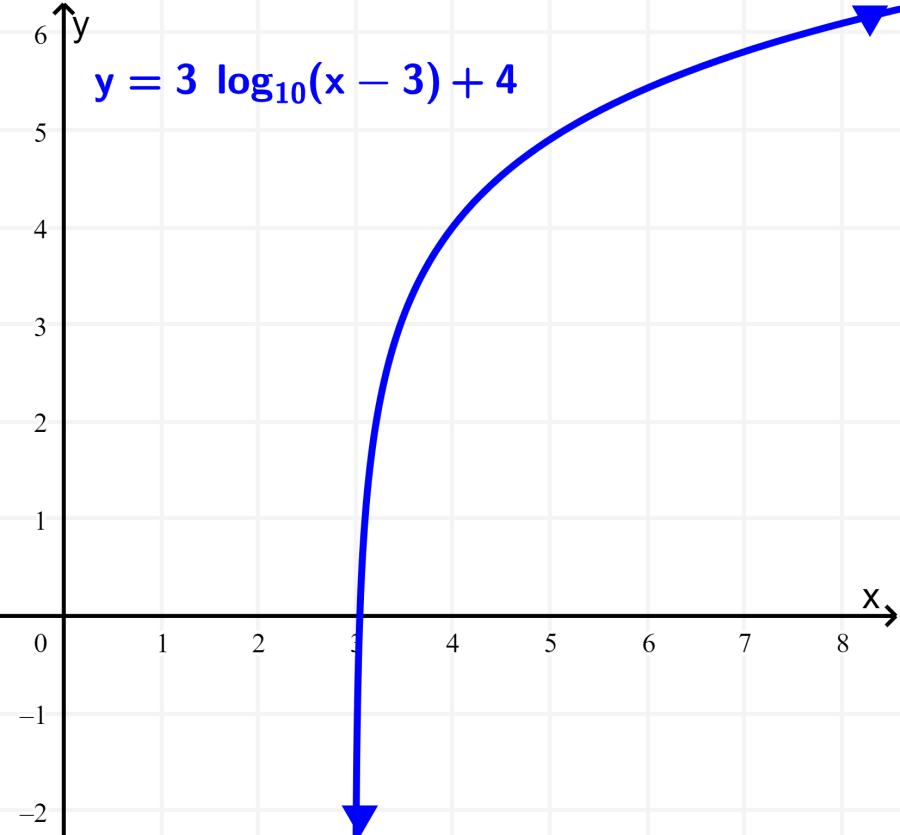
Calcula el dominio y el rango de la función $latex f(x)=3\log(x-3)+4$.
Solución: El 3 representa un estiramiento de la gráfica y el 4 representa una traslación vertical de la gráfica. Estos dos valores no afectan ni al dominio ni al rango de la función logarítmica, por lo que tanto el dominio como el rango siguen siendo los mismos que en el anterior ejemplo:
Dominio: $latex 3<x<\infty$
Rango: $latex -\infty<x<\infty$
EJEMPLO 4
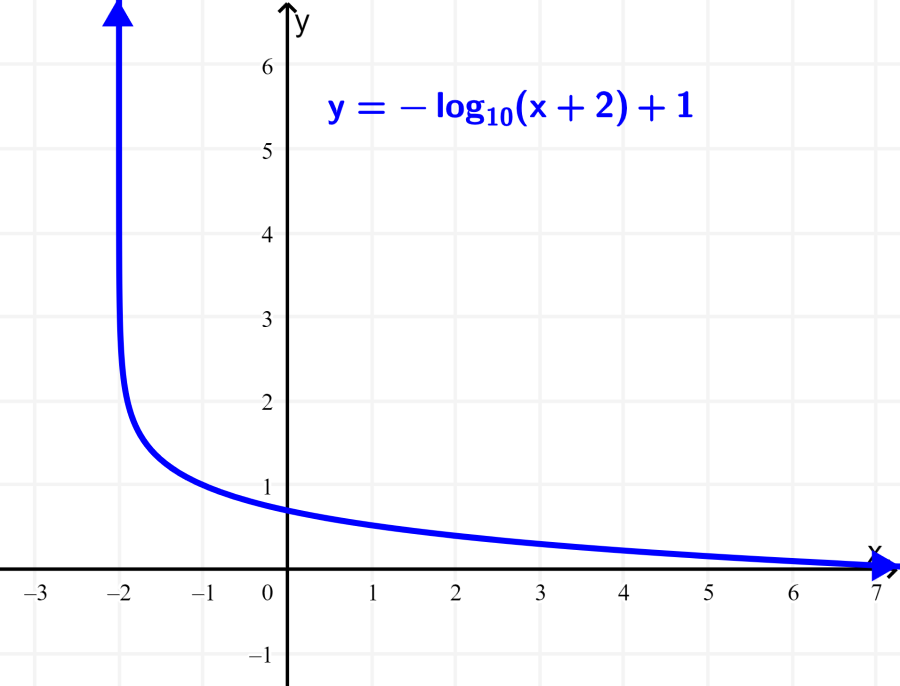
¿Cuál es el dominio y el rango de la función $latex f(x)=-\log(x+2)+1$?
Solución: Esta función tiene una gráfica que es reflejada con respecto al eje x. Sin embargo, esto no cambia ni al dominio ni al rango. El único valor que afecta al dominio es el -2, el cual produce una traslación hacia la izquierda de 2 unidades tanto a la función como a su asíntota. Entonces, el dominio es:
Dominio: $latex -2<x<\infty$
Véase también
¿Interesado en aprender más sobre funciones logarítmicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
