El dominio de funciones lineales es igual a todo el conjunto de números reales de x. Esto se debe a que no tenemos ninguna restricción en los valores de x. De igual forma, el rango de funciones lineales también es todo el conjunto de números reales de y.
A continuación, veremos más detalles sobre el rango y el dominio de funciones lineales. También, veremos algunos ejemplos que nos ayudarán a visualizar el dominio y rango de funciones lineales.
¿Qué es el dominio?
El dominio es el conjunto de todos los valores posibles que puede tener la variable independiente. Generalmente, el dominio es definido como todos los valores posibles de x.
El dominio puede ser determinado al encontrar valores que hagan que la función sea indefinida y extraer esos valores del dominio. En la mayoría de los casos, esto incluye evitar tener denominadores que sean iguales a cero, ya que la división por cero es indefinida.
También, tenemos que evitar tener un valor negativo dentro de una raíz cuadrada u otras raíces pares, ya que esto resultará en números imaginarios.
¿Qué es el rango?
El rango es definido como todos los valores posibles de la variable dependiente que son obtenidos al usar todos los valores del dominio como entrada. Podemos considerar al rango como todos los valores posibles de y.
Encontrar el rango es un poco más complicado, ya que primero debemos tener conocimiento sobre el dominio. Para facilitar encontrar el rango, podemos graficar la función con una calculadora gráfica o trazar una gráfica simple de la función para tener una idea de lo que puede ser su rango.
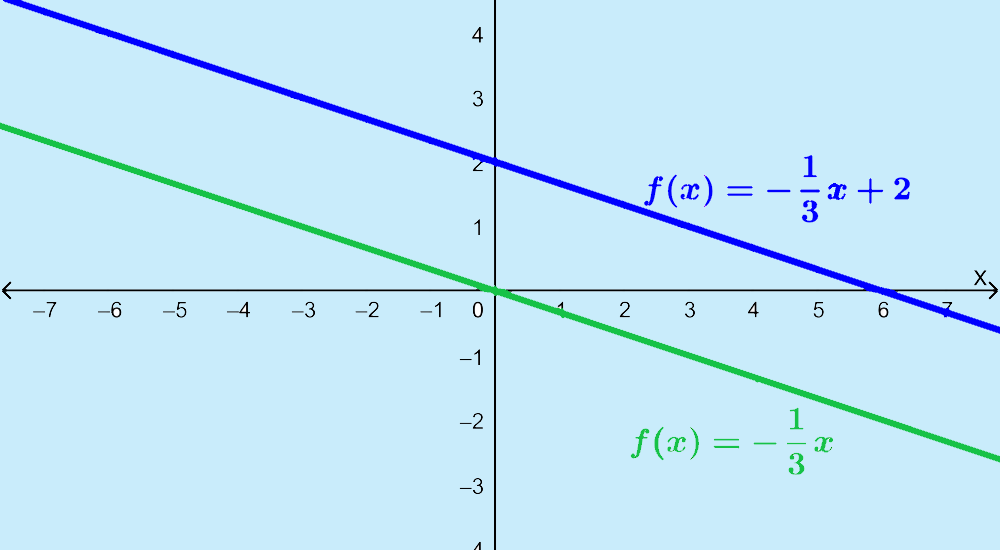
Dominio y rango de funciones lineales
Para encontrar el dominio de una función lineal, identificamos si es que tenemos denominadores que podrían volverse cero o raíces cuadradas que podrían contener valores negativos. Sabemos que la forma general de una función lineal es $latex f(x)=ax+b$.
Una función lineal no está compuesta de denominadores ni raíces cuadradas, por lo que no tenemos ninguna restricción en el dominio de la función. Eso significa que el dominio es igual a todos los números reales. Esto puede ser representado en notación de conjuntos como:
$latex \{x|x\in R\}$
Y en notación de intervalos como:
$latex (-\infty, \infty)$
La gráfica de una función lineal es una línea recta. Estas funciones no tienen ninguna restricción, por lo que crecen de “menos” infinito a “más” infinito. Eso significa que el rango también es igual a todos los números reales y en notación de conjuntos, tenemos:
$latex \{y|y\in R\}$
EJEMPLO 1
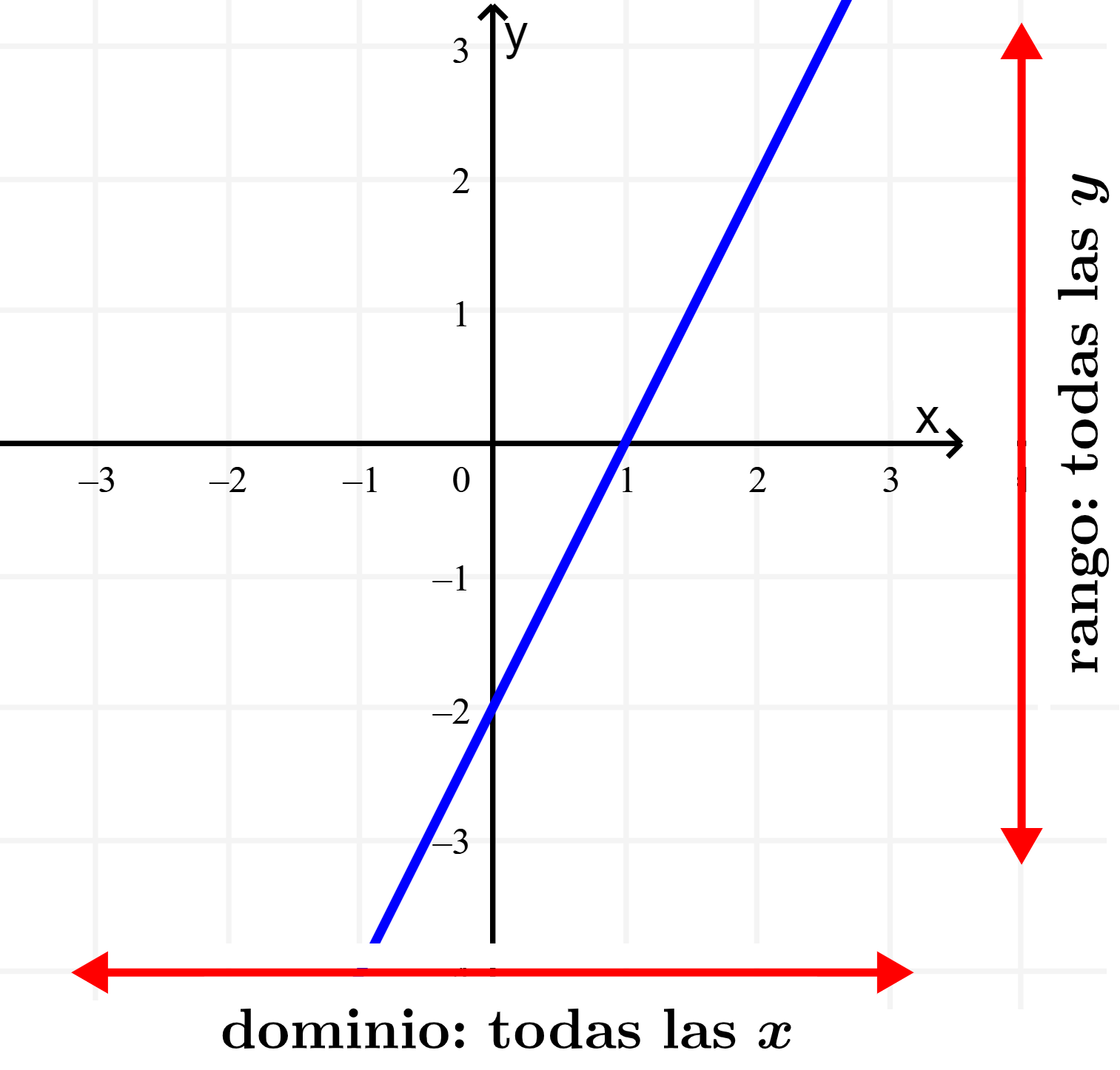
Encuentra el dominio y el rango de la función lineal $latex y=2x-2$.
Solución: Lo primero que podemos observar es que no tenemos raíces cuadradas o denominadores. Esto significa que no tendremos problemas con números negativos en raíces cuadradas o ceros en denominadores.
Por lo tanto, fácilmente podemos determinar que el dominio es todos los números reales de x. La siguiente tabla muestra el dominio y el rango de esta función:
Dado que la gráfica de la función es una línea, podemos predecir que el rango es todos los valores reales de y. La línea puede ir tan alto o tan bajo como quiera sin límites. Podemos observar esto en la gráfica de la función:
EJEMPLO 2
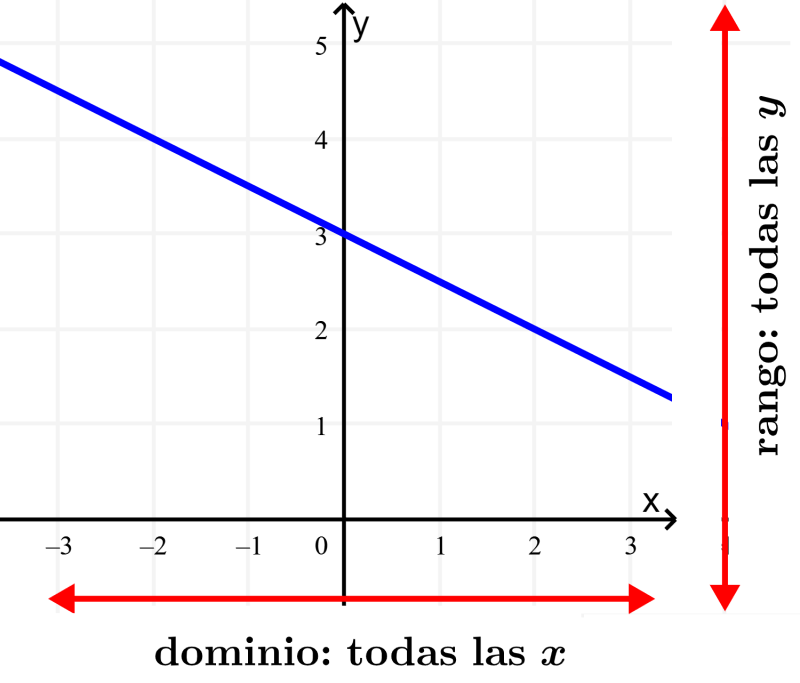
Determina el dominio y el rango de la función lineal $latex y=-\frac{1}{2}x+3$.
Solución: Similar al anterior problema, no tenemos ni raíces cuadradas ni denominadores. Por lo tanto, sabemos que no estamos restringidos a ningún valor y el dominio es todos los números reales de x. Esto será verdadero con todas las funciones lineales. La siguiente tabla muestra el dominio y el rango de esta función:
De igual forma, sabemos que el rango será todos los valores reales de y. En la gráfica de la función, podemos ver que la línea puede resultar en cualquier valor de y. Este siempre será el caso para las funciones lineales.
Véase también
¿Interesado en aprender más sobre funciones lineales? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
