Las funciones cuadráticas son algunas de las relaciones que siempre encontraremos en el estudio del álgebra. Y una de las características importantes de estas funciones es su dominio y rango. A continuación, empezaremos con una revisión rápida de lo que representan el dominio y el rango.
Luego, aprenderemos a encontrar el dominio y el rango de funciones cuadráticas. También, veremos varios ejercicios resueltos para dominar este tema completamente.
ÁLGEBRA
Relevante para…
Aprender sobre el dominio y el rango de funciones cuadráticas.
ÁLGEBRA
Relevante para…
Aprender sobre el dominio y el rango de funciones cuadráticas.
Resumen de dominio y rango
Dominio de una función
El dominio de una función es el conjunto de todos los valores posibles de la variable independiente, que son comúnmente conocidos como los valores de x.
Podemos encontrar el dominio al identificar valores particulares de x que hacen que la función tenga comportamientos “indebidos” y tenemos que excluir esos valores.
Para determinar el dominio, especialmente buscamos valores de x que hagan que el denominador sea cero, ya que no podemos tener división por cero y valores que hagan que tengamos números negativos dentro de raíces cuadradas.
Rango de una función
El rango de una función es el conjunto de todos los valores de salida que son obtenidos al usar los valores de x en el dominio. Esto significa que necesitamos encontrar al dominio primero para describir al rango. El rango es conocido comúnmente como los valores de x.
Encontrar el rango es un poco más difícil que encontrar el dominio. Para facilitar esto, es recomendable graficar la función con una calculadora gráfica o intentar obtener una gráfica básica de la función a mano.
Es importante tener una idea de cómo se verá la gráfica para describir el rango de la función correctamente.
¿Cómo encontrar el dominio y el rango de una función cuadrática?
El dominio de funciones cuadráticas puede ser encontrado al determinar cuáles valores de x podemos usar y cuáles no. Específicamente, debemos evitar valores de x que hacen que la función tenga denominadores iguales a cero, ya que producirían división por cero.
También, debemos evitar valores de x que hacen que tengamos valores negativos dentro de la raíz cuadrada u otras raíces impares. En el caso de funciones cuadráticas, no tenemos ni denominadores ni raíces cuadradas, por lo que no tenemos restricciones con el dominio.
Eso significa que el dominio es igual a todos los números reales de x. En notación de conjuntos esto es representado como:
$latex \{x|x\in R\}$
En notación de intervalos esto es representado como:
$latex (- \infty, +\infty)$
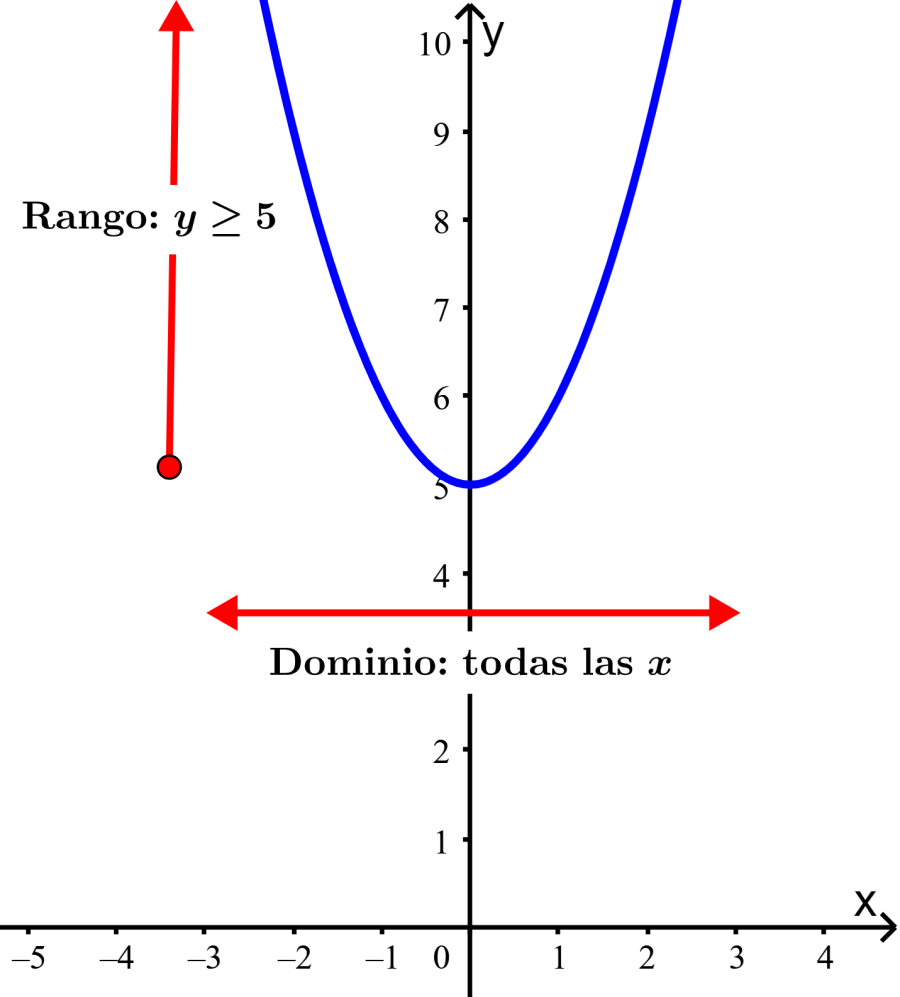
Sabemos que las gráficas de funciones cuadráticas tienen máximos o mínimo. Entonces, para encontrar el rango de una función cuadrática, tenemos que determinar su punto máximo o mínimo. Esto puede ser encontrado fácilmente al realizar una gráfica básica de la función.
Alternativamente, el rango puede ser encontrado al determinar algebraicamente el vértice de la gráfica de la función y determinar si la gráfica se abre hacia abajo o hacia arriba.
La gráfica se abre hacia arriba si es que el coeficiente del término cuadrático es positivo y se abre hacia abajo si es que el coeficiente del término cuadrático es negativo.
Ejercicios de dominio y rango de funciones cuadráticas resueltos
Los siguientes ejercicios pueden ser usados para entender el proceso aplicado para encontrar el dominio y el rango de funciones cuadráticas. Intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Encuentra el dominio y el rango de la función $latex f(x)={{x}^2}+2$.
Solución
Al usar varios valores de x, podemos comprobar que no estamos restringidos con ningunos valores, por lo que el dominio de esta función es todos los números reales.
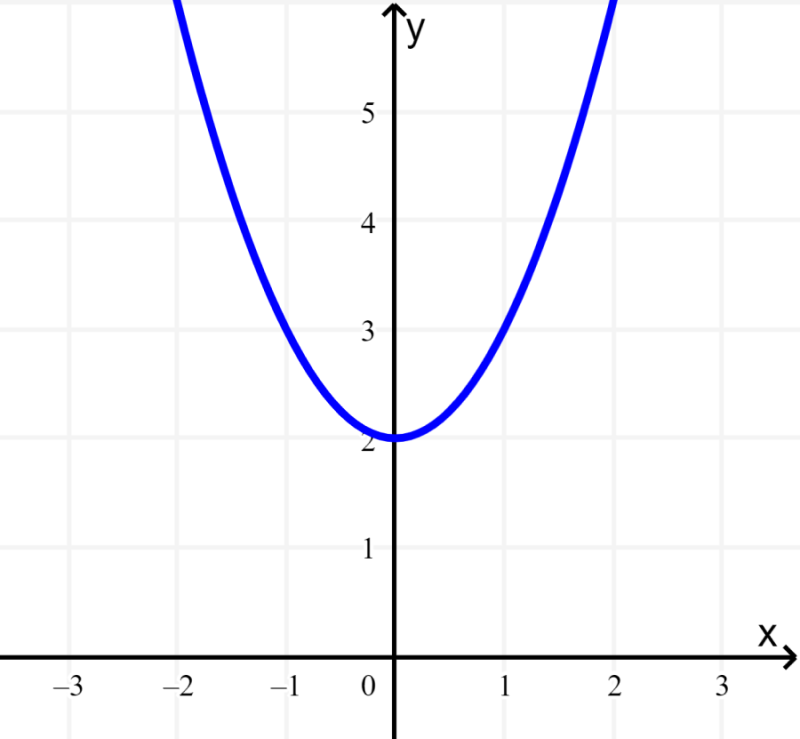
Determinar el rango es un poco más complicado. Podemos trazar una gráfica de esta función para observar cuál es su punto mínimo o máximo:
En la gráfica, podemos ver que el valor mínimo del rango es $latex y=2$ y la función tiene valores mayores que eso. Esto significa que el rango de la función es $latex y\geq 2$.
EJERCICIO 2
Encuentra el dominio y el rango de la función cuadrática $latex f(x)=-{{x}^2}+4$.
Solución
El dominio de esta función es todos los números reales, ya que no existen valores de x que harán que la función produzca valores “inapropiados”.
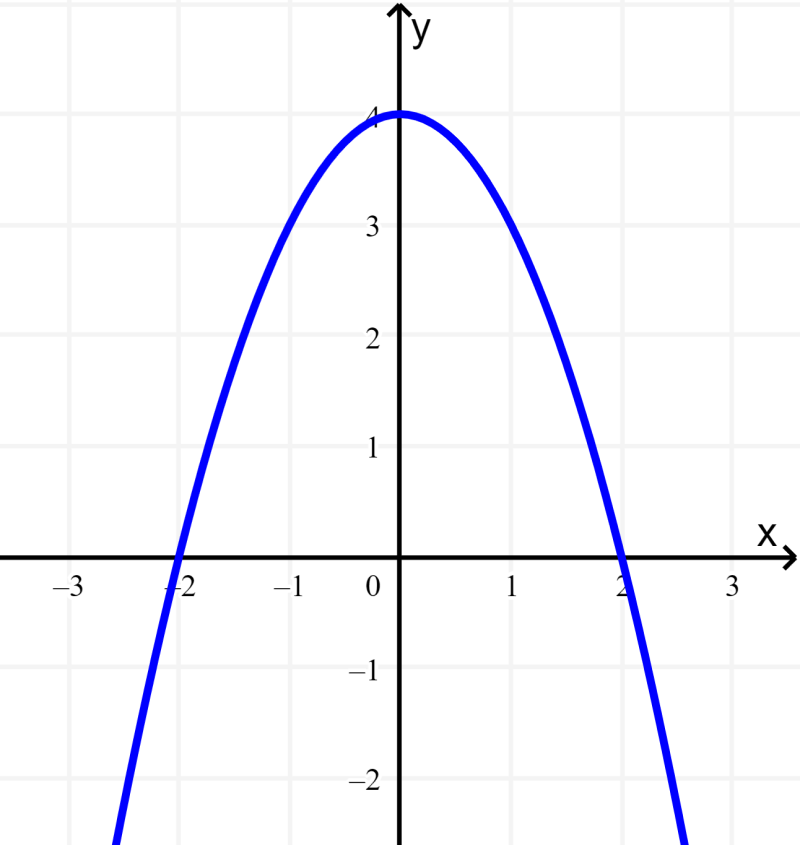
Para determinar el dominio, trazamos una gráfica básica de esta función:
Vemos que esta gráfica se abre hacia abajo. La gráfica tiene un punto máximo en $latex y=4$ y toma todos los valores menores a $latex y=4$. Entonces, el rango de esta función es $latex y\leq 4$.
EJERCICIO 3
Determina el dominio y el rango de la función $latex f(x)={{x}^2}+4x-1$.
Solución
De los ejercicios anteriores, ya podemos darnos cuenta de que las funciones cuadráticas tienen un dominio que es igual a todos los valores de x.
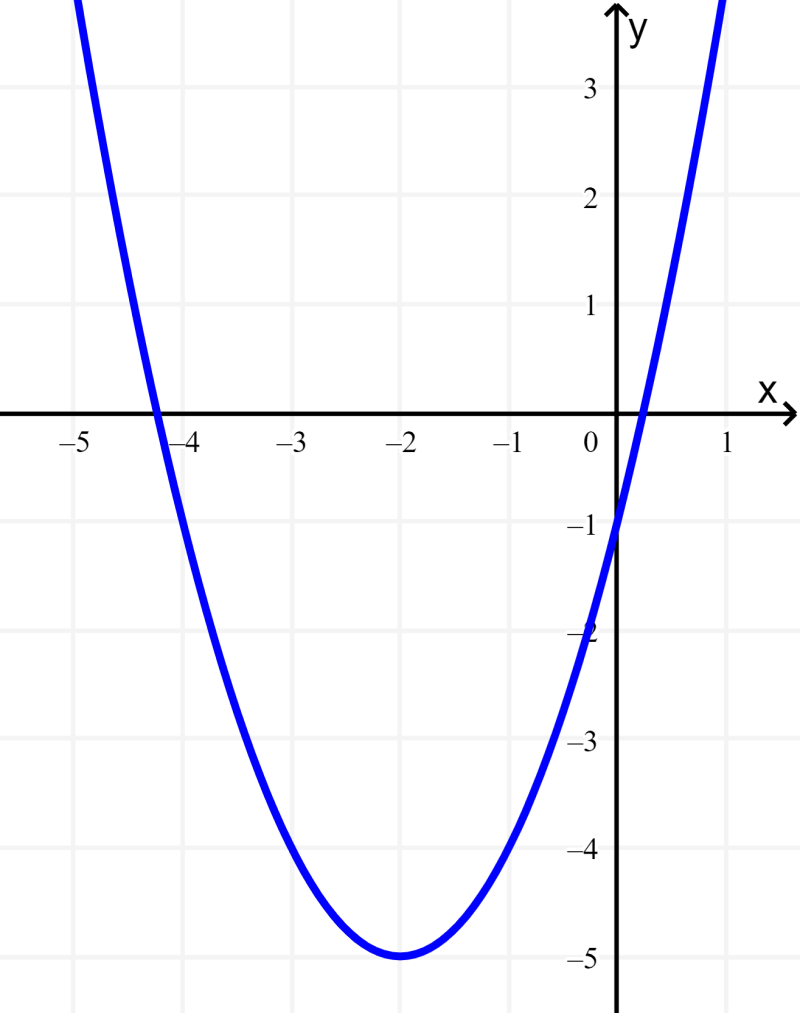
Para encontrar el rango de la función, podemos o bien graficar o reescribir la función en su forma vértice y encontrar el punto máximo o mínimo.
La función está dada en la forma estándar $latex f(x)=a{{x}^2}+bx+c$, por lo que ahora vamos a convertirla a la forma vértice $latex f(x)=a{{(x-h)}^2}+k$, en donde, $latex (h, k)$ es el vértice. Entonces, completando el cuadrado, tenemos:
$latex f(x)={{x}^2}+4x-1$
$latex =({{x}^2}+4x)-1$
$latex =({{x}^2}+4x+4)-1-4$
$latex ={{(x+2)}^2}-5$
El término cuadrático de esta función es positivo, por lo que su gráfica se abre hacia arriba. Esto significa que el vértice, que es igual a $latex (-2, -5)$, representa al punto mínimo. Entonces, el rango es $latex y\geq -5$.
EJERCICIO 4
Encuentra el rango de la función $latex f(x)=2{{x}^2}+12x+16$.
Solución
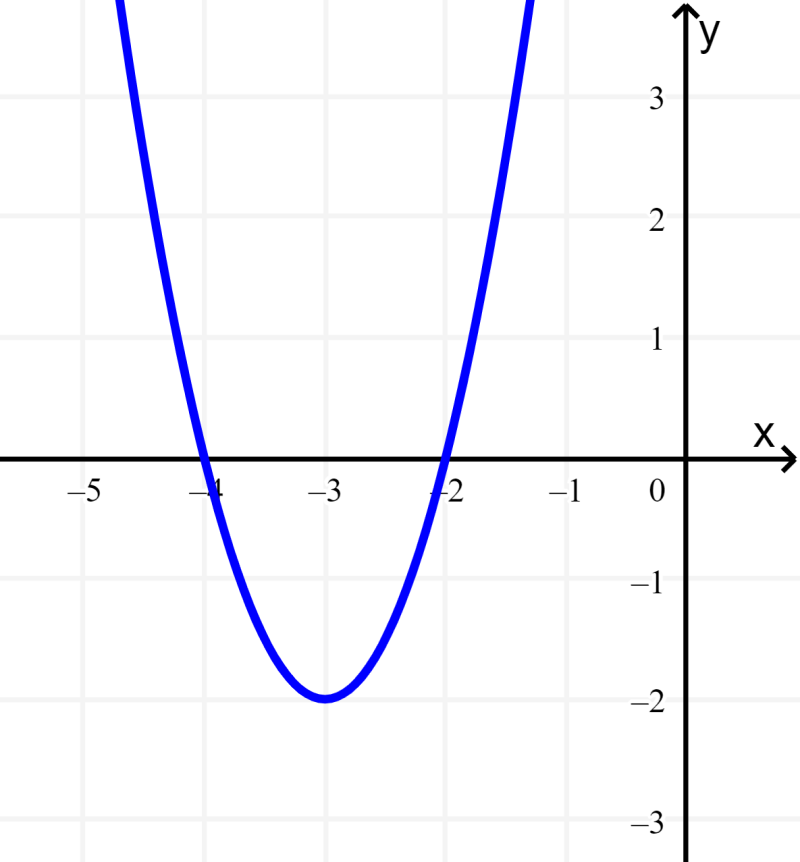
Adicional a usar el método de completar el cuadrado para encontrar el vértice, también podemos usar fórmulas para encontrar el vértice directamente. Las coordenadas de h y k del vértice de la gráfica están dadas por:
$latex h=\frac{-b}{2a}=\frac{-12}{2(2)}=-3$
$latex k=f(-3)=-2$
El coeficiente del término cuadrático es positivo, lo que significa que la gráfica de la función se abre hacia arriba y el vértice $latex (-3, -2)$ representa al punto mínimo. El rango de la función es $latex y\geq -2$.
Ejercicios de dominio y rango de funciones cuadráticas para resolver
Pon en práctica tu conocimiento sobre dominio y rango para resolver los siguientes ejercicios. Si necesitas ayuda puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre funciones cuadráticas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
