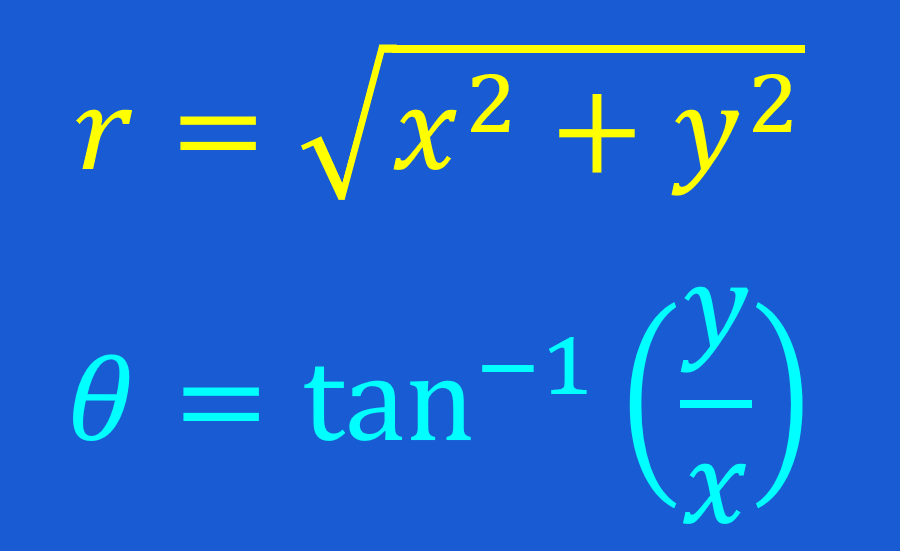Las coordenadas polares son escritas de la forma (r, θ), en donde, r es la distancia y θ es el ángulo. Estas coordenadas pueden ser relacionadas con las coordenadas rectangulares o cartesianas usando trigonometría, un triángulo rectángulo y el teorema de Pitágoras. Resulta que usamos la función tangente para encontrar al ángulo y el teorema de Pitágoras para encontrar a la distancia, r.
A continuación, conoceremos las fórmulas que podemos usar para transformar de coordenadas rectangulares a polares. También, resolveremos algunos ejercicios de práctica para aplicar las fórmulas aprendidas.
TRIGONOMETRÍA
Relevante para…
Aprender a transformar de coordenadas rectangulares a polares.
TRIGONOMETRÍA
Relevante para…
Aprender a transformar de coordenadas rectangulares a polares.
¿Cómo transformar de coordenadas rectangulares a coordenadas polares?
Recordamos que las coordenadas rectangulares son escritas de la forma $latex (x, y)$ y las coordenadas polares son escritas de la forma $latex (r, \theta)$, en donde, r es la distancia desde el origen hasta el punto y θ es el ángulo formado por la línea y el eje x. Estas coordenadas son relacionadas usando trigonometría.
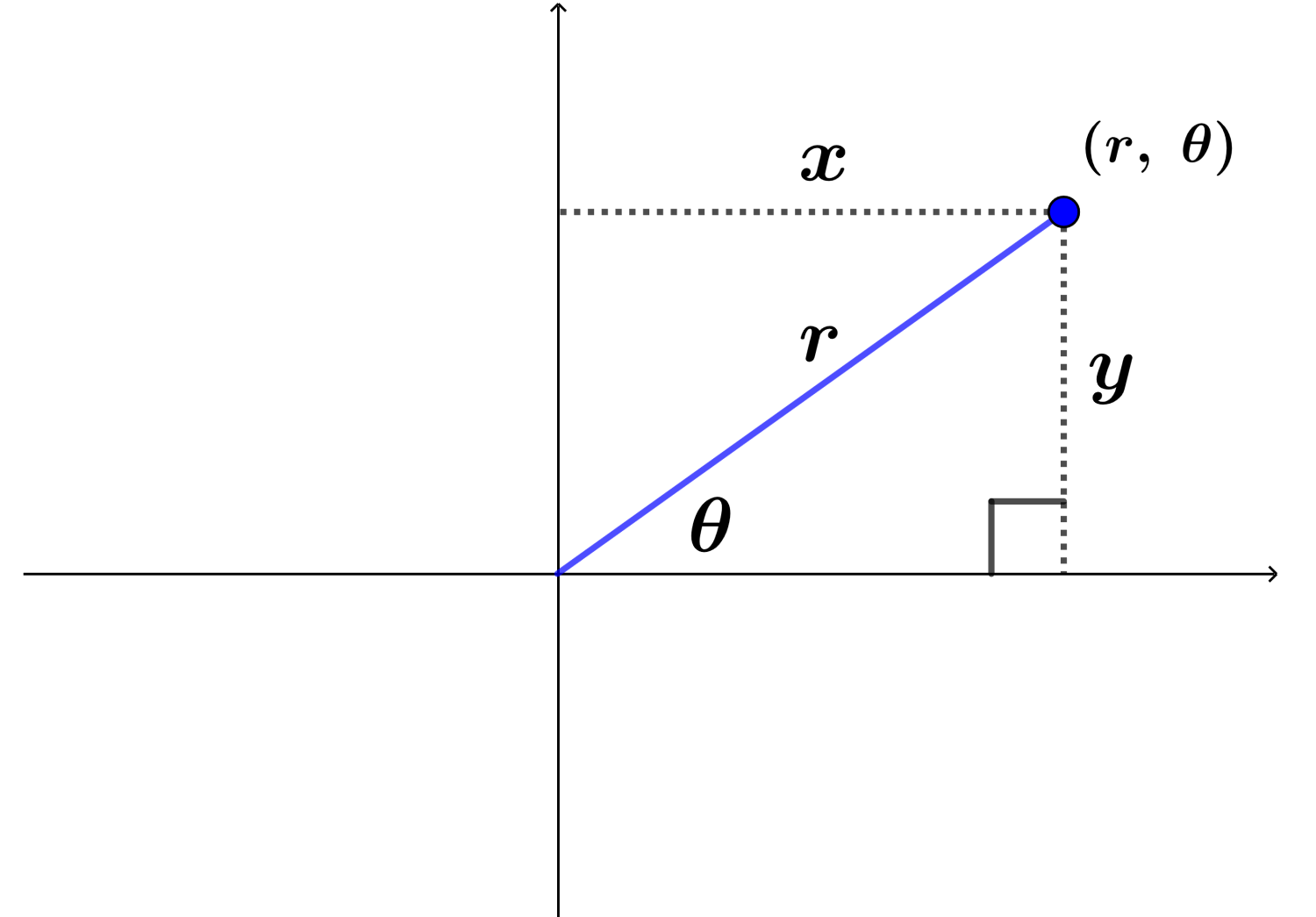
Observemos el siguiente diagrama:
Usando el triángulo rectángulo, podemos obtener relaciones para las coordenadas polares en términos de las coordenadas rectangulares. Observamos que las coordenadas en x forman la base del triángulo rectángulo y las coordenadas en y forman la altura.
Además, vemos que la distancia r corresponde a la hipotenusa del triángulo. Entonces, podemos usar el teorema de Pitágoras para encontrar la longitud de la hipotenusa:
$latex {{r}^2}={{x}^2}+{{y}^2}$
| $latex r=\sqrt{{{x}^2}+{{y}^2}}$ |
El ángulo θ puede ser encontrado usando la función tangente. Recordemos que la tangente de un ángulo es igual al lado opuesto dividido por el lado adyacente. El lado opuesto es el componente y y el lado adyacente es el componente x. Entonces, tenemos:
| $latex \theta=\tan^{-1}(\frac{y}{x})$ |
Debido a que el rango de la función tangente inversa va desde $latex -\frac{\pi}{2}$ hasta $latex \frac{\pi}{2}$, esto no cubre los cuatro cuadrantes del plano cartesiano, por lo que muchas veces, la calculadora puede dar el valor incorrecto de $latex {{\tan}^{-1}}$.
Esto depende en el cuadrante en el que se ubica el punto. Podemos usar lo siguiente para arreglar esto:
| Cuadrante | Valor de $latex {{\tan}^{-1}}$ |
| I | Usamos el valor de la calculadora |
| II | Sumamos 180° al valor de la calculadora |
| III | Sumamos 180° al valor de la calculadora |
| IV | Sumamos 360° al valor de la calculadora |
→ Cursos Gratis: Explora Nuestros Cursos de Matemáticas
Ejercicios de coordenadas rectangulares a polares resueltos
Lo aprendido sobre la transformación de coordenadas rectangulares a coordenadas polares es usado para resolver los siguientes ejercicios. Intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Si es que tenemos las coordenadas rectangulares (3, 4), ¿cuál es su equivalente en coordenadas polares?
Solución
Tenemos los valores $latex x=3, ~y=4$. Usamos las fórmulas dadas arriba junto con estos valores para encontrar las coordenadas polares. Entonces, el valor de r es encontrado usando el teorema de Pitágoras:
$latex r=\sqrt{{{x}^2}+{{y}^2}}$
$latex r=\sqrt{{{3}^2}+{{4}^2}}$
$latex r=\sqrt{9+16}$
$latex r=\sqrt{25}$
$latex r=5$
Ahora, encontramos el valor de θ usando la tangente inversa:
$latex \theta={{\tan}^{-1}}(\frac{y}{x})$
$latex \theta={{\tan}^{-1}}(\frac{4}{3})$
$latex \theta=0.93$ rad
Tanto el componente en x como el componente en y son positivos, por lo que el punto está en el primer cuadrante. Esto significa que el ángulo obtenido es el correcto.
Las coordenadas polares son (5, 0.93 rad).
EJERCICIO 2
Tenemos las coordenadas rectangulares (-1, 3). ¿Cuál es su equivalente en coordenadas polares?
Solución
Podemos observar los valores $latex x=-1, ~y=3$. Encontramos el valor de r usando el teorema de Pitágoras junto con los valores dados:
$latex r=\sqrt{{{x}^2}+{{y}^2}}$
$latex r=\sqrt{{{(-1)}^2}+{{3}^2}}$
$latex r=\sqrt{1+9}$
$latex r=\sqrt{10}$
Para encontrar el valor de θ, usamos la tangente inversa:
$latex \theta={{\tan}^{-1}}(\frac{y}{x})$
$latex \theta={{\tan}^{-1}}(\frac{3}{-1})$
$latex \theta=-1.25$ rad
El componente en x es negativo y el componente en y es positivo, por lo que el punto está en el segundo cuadrante. Esto significa que tenemos que sumar π al ángulo obtenido. El ángulo correcto es $latex \theta=-1.25+\pi=1.89$ rad.
Las coordenadas polares son ($latex \sqrt{10}$, 1.89 rad).
EJERCICIO 3
Si es que tenemos las coordenadas cartesianas (-3, -9), ¿cuáles son las coordenadas polares?
Solución
Tenemos los valores $latex x=-3, ~y=-9$. El valor de r es encontrado usando el teorema de Pitágoras:
$latex r=\sqrt{{{x}^2}+{{y}^2}}$
$latex r=\sqrt{{{(-3)}^2}+{{(-9)}^2}}$
$latex r=\sqrt{9+81}$
$latex r=\sqrt{90}$
$latex r=3\sqrt{10}$
El valor de θ es:
$latex \theta={{\tan}^{-1}}(\frac{y}{x})$
$latex \theta={{\tan}^{-1}}(\frac{-9}{-3})$
$latex \theta=1.25$ rad
Tanto el componente en x como el componente en y son negativos, por lo que el punto está en el tercer cuadrante. Esto significa que tenemos que sumar π al ángulo obtenido. El ángulo correcto es $latex \theta=1.25+\pi=4.39$ rad.
Las coordenadas polares son ($latex 3\sqrt{10}$, 1.25 rad).
EJERCICIO 4
Un punto está definido por (4, -5) en coordenadas rectangulares. ¿Cómo podemos definir al punto en coordenadas polares?
Solución
Podemos extraer los valores $latex x=4, ~y=-5$. Usamos estos valores y el teorema de Pitágoras para encontrar el valor de r:
$latex r=\sqrt{{{x}^2}+{{y}^2}}$
$latex r=\sqrt{{{4}^2}+{{(-5)}^2}}$
$latex r=\sqrt{16+25}$
$latex r=\sqrt{41}$
Ahora, usamos la tangente inversa para encontrar el valor de θ:
$latex \theta={{\tan}^{-1}}(\frac{y}{x})$
$latex \theta={{\tan}^{-1}}(\frac{4}{-5})$
$latex \theta=-0.67$ rad
El componente en x es positivo y el componente en y es negativo, por lo que el punto está en el cuarto cuadrante. Esto significa que tenemos que sumar 2π al ángulo obtenido. El ángulo correcto es $latex \theta=-0.67+2\pi=5.61$ rad.
Las coordenadas polares son ($latex \sqrt{41}$, -0.67 rad).
Únete a nuestros cursos interactivos o practica con nuestros generadores de problemas
Ejercicios de coordenadas rectangulares a polares para resolver
Resuelve los siguientes ejercicios usando las fórmulas vistas arriba para transformar de coordenadas rectangulares a polares. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
→ Explora más ejercicios de práctica
Véase también
¿Interesado en aprender más sobre coordenadas polares y otros sistemas? Mira estas páginas:
