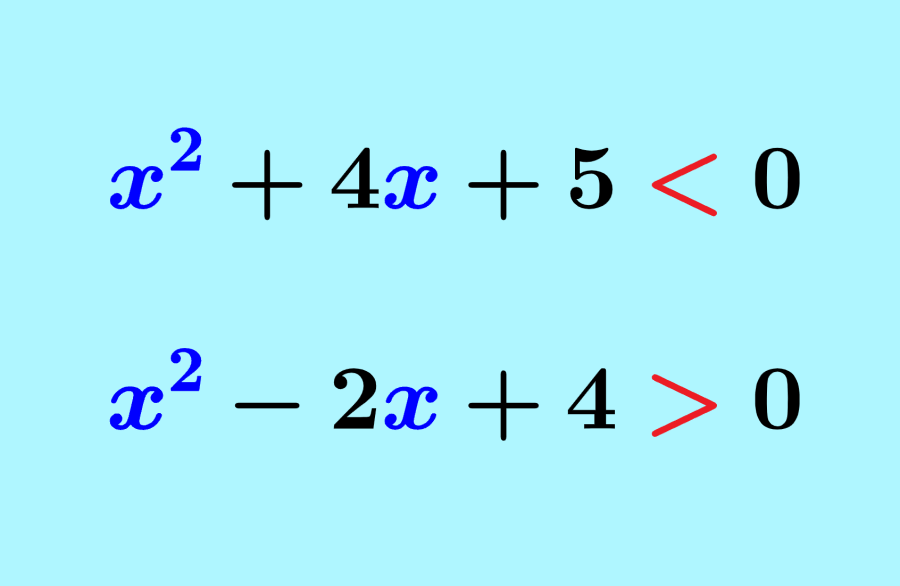Las desigualdades cuadráticas tienen la forma ax²+bx+c<0. Las desigualdades pueden usar los signos de mayor que, menor que, mayor o igual que y menor o igual que. Para resolver este tipo de desigualdades, tenemos que determinar los puntos en los que la gráfica de la función cuadrática cortará al eje x. Trazar una gráfica simple siempre es útil.
A continuación, aprenderemos todo lo relacionado con las desigualdades cuadráticas. Conoceremos cómo resolverlas y aplicaremos lo aprendido en unos ejercicios de práctica.
Cómo resolver desigualdades cuadráticas
Para resolver desigualdades cuadráticas, podemos seguir los siguientes pasos:
Paso 1: Simplificar y escribir a la desigualdad en la forma $latex ax^2+bx+c<0$. El signo «<» podría ser diferente dependiendo del problema.
Paso 2: Identificar en dónde la gráfica de $latex y=ax^2+bx+c$ corta al eje x. Para lograr esto, podemos factorizar la expresión cuadrática $latex ax^2+bx+c=0$ y encontrar los valores de x.
Paso 3: Trazar una gráfica simple de la función $latex y=ax^2+bx+c$ para determinar la solución. Alternativamente, podemos resolver sin una gráfica considerando lo siguiente:
- Si es que tenemos un término cuadrático positivo, la parábola se abre hacia arriba y tiene una forma de U.
- Si es que el término cuadrático es negativo, la parábola se abre hacia abajo.
- Los valores debajo del eje x son menores que 0 y los valores encima del eje x son mayores que 0.
Paso 4: Usando la gráfica o de otra forma, tenemos que determinar los símbolos de desigualdad que harán que las soluciones encontradas en el paso 2 satisfagan la desigualdad.
Explora los ejercicios resueltos mostrados a continuación para entender la aplicación de estos pasos con problemas reales.
10 Ejercicios de desigualdades cuadráticas resueltos
EJERCICIO 1
Resuelve la desigualdad $latex x^2+3x-4<0$.
Solución
Para resolver la desigualdad, tenemos que encontrar las raíces de la ecuación $latex x^2+3x-4=0$. Podemos lograr esto usando factorización:
$latex x^2+3x-4=0$
$latex (x+4)(x-1)=0$
$latex x=-4~~$ o $latex ~~x=1$
Ahora, podemos trazar una gráfica para facilitar la resolución del problema:
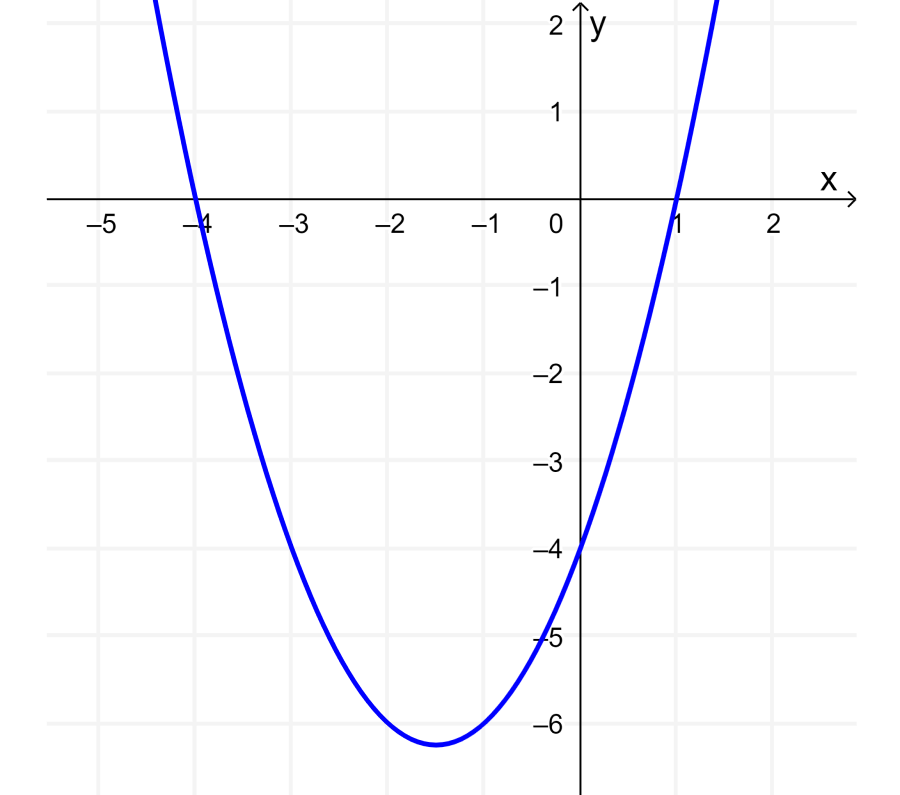
Tenemos la desigualdad $latex x^2+3x-4<0$, la cual nos indica que necesitamos la parte que tiene valores menores que 0. Es decir, necesitamos la parte que está debajo del eje x.
Usando la gráfica, podemos deducir que esto sucede cuando $latex -4<x<1$.
EJERCICIO 2
Encuentra la solución a la desigualdad $latex x^2+x-2>0$.
Solución
Para resolver la desigualdad, tenemos que empezar encontrando los valores de x en la ecuación $latex x^2+x-2=0$. Entonces, podemos usar factorización:
$latex x^2+x-2=0$
$latex (x+2)(x-1)=0$
$latex x=-2~~$ o $latex ~~x=1$
La parábola formada por la ecuación $latex y=x^2+x-2$ se abre hacia arriba y tiene forma de U porque el término cuadrático es positivo:
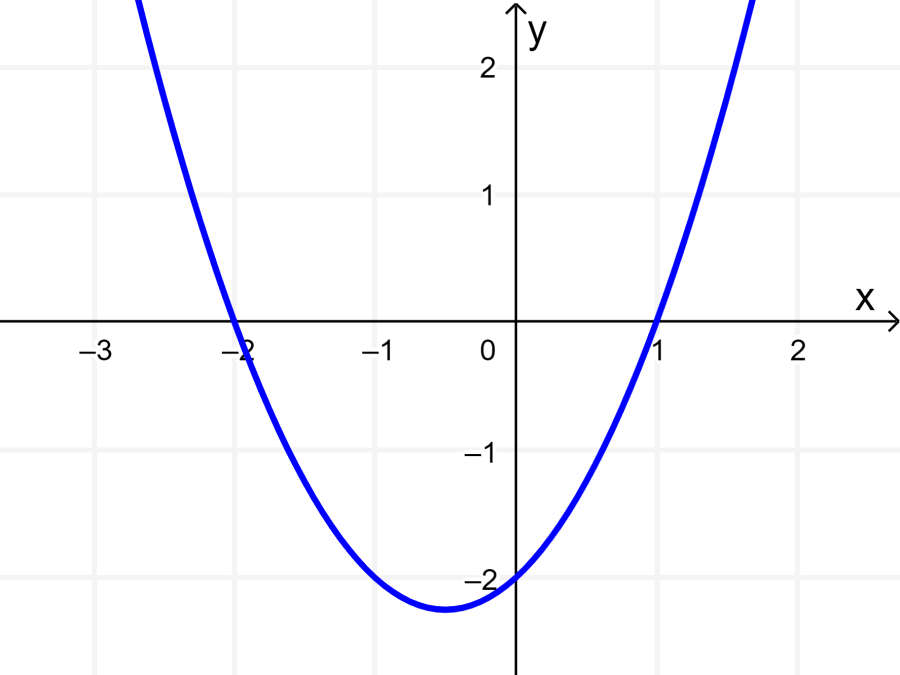
La desigualdad $latex x^2+x-2>0$ indica que los valores siempre son mayores que 0. Usando la gráfica, podemos deducir que esto sucede cuando $latex x<-2~$ o $latex ~x>1$.
EJERCICIO 3
Resuelve la desigualdad $latex x^2+2x-8<0$.
Solución
Tenemos que encontrar los valores de x en la ecuación $latex x^2+2x-8=0$. Podemos lograr esto usando factorización:
$latex x^2+2x-8=0$
$latex (x+4)(x-2)=0$
$latex x=-4~~$ o $latex ~~x=2$
Vamos a resolver sin usar la gráfica. Para esto, tenemos que considerar que dado que el término cuadrático es positivo, la parábola formada por $latex y=x^2+2x-8$ se abrirá hacia arriba.
Ahora, la desigualdad $latex x^2+2x-8<0$ indica que necesitamos solo los valores que son menor que 0, es decir, la parte que está debajo del eje x. Esto sucede cuando $latex -4<x<2$.
EJERCICIO 4
Encuentra la solución a la desigualdad $latex x^2+8x+4>2x-4$.
Solución
Empezamos simplificando de la siguiente forma:
$latex x^2+8x+4>2x-4$
$latex x^2+6x+8>0$
Ahora, podemos formar la ecuación $latex x^2+6x+8=0$ y resolver por factorización:
$latex x^2+6x+8=0$
$latex (x+4)(x+2)=0$
$latex x=-4~~$ o $latex ~~x=-2$
La desigualdad $latex x^2+6x+8>0$ significa que los valores siempre son mayores que 0. Esto significa que necesitamos la parte de la parábola que está encima del eje x.
Dado que la parábola se abre hacia arriba (el término cuadrático es positivo), la solución a la desigualdad es $latex x<-4~$ o $latex ~x>-2$.
EJERCICIO 5
Resuelve la desigualdad $latex x^2+2x-12<x+8$.
Solución
Podemos combinar términos semejantes y escribir a la desigualdad en la forma $latex ax^2+bx+c<0$:
$latex x^2+2x-12<x+8$
$latex x^2+x-20<0$
Podemos encontrar los valores de x al formar la ecuación $latex x^2+x-20=0$ y resolver usando factorización:
$latex x^2+x-20=0$
$latex (x+5)(x-4)=0$
$latex x=-5~~$ o $latex ~~x=4$
Ahora, tenemos que encontrar los valores de x que hagan que $latex x^2+x-20<0$ tenga siempre valores menores que 0. Esto significa que necesitamos la parte debajo del eje x.
Dado que la parábola se abre hacia arriba (el término cuadrático es positivo), la parábola está debajo del eje x cuando los valores de x son mayores que -5 y menores que 4, es decir, $latex -5<x<4$.
EJERCICIO 6
¿Cuál es la solución a la desigualdad $latex x^2+4x+10>-4x-5$?
Solución
Al simplificar la desigualdad, obtenemos lo siguiente:
$latex x^2+4x+10>-4x-5$
$latex x^2+8x+15>0$
Ahora, podemos formar la ecuación $latex x^2+8x+15=0$ y resolverla por factorización:
$latex x^2+8x+15=0$
$latex (x+5)(x+3)=0$
$latex x=-5~~$ o $latex ~~x=-3$
Para resolver la desigualdad $latex x^2+8x+15>0$, tenemos que encontrar los valores de x que siempre producen valores mayores que 0 (encima del eje x)
Dado que la parábola se abre hacia arriba, la solución a la desigualdad es $latex x<-5~$ o $latex ~x>-3$.
EJERCICIO 7
Resuelve la desigualdad $latex -x^2+6x-8\geq 0$.
Solución
Aquí, tenemos un término cuadrático que es negativo. Podemos facilitar la resolución de la desigualdad al multiplicar a toda la desigualdad por -1 para lograr que el término cuadrático sea positivo:
$latex x^2-6x+8\leq 0$
Nota: Ten en cuenta que al multiplicar o dividir a la desigualdad por un signo negativo, tenemos que darle la vuelta al signo de desigualdad.
Ahora, formamos la ecuación $latex x^-6x+8=0$ y resolvemos por factorización para encontrar los valores de x:
$latex x^2-6x+8=0$
$latex (x-4)(x-2)=0$
$latex x=4~~$ o $latex ~~x=2$
Para resolver la desigualdad $latex x^2-6x+8\leq 0$, tenemos que buscar los valores de x que produzcan valores menores o iguales a 0. Entonces, buscamos la porción de la parábola debajo del eje x.
La solución es $latex 2\leq x\leq 4$.
EJERCICIO 8
Encuentra la solución a la desigualdad $latex -2x^2+9x-10\leq 0$.
Solución
Nuevamente, podemos multiplicar a toda la desigualdad por -1 para facilitar su resolución:
$latex 2x^2-9x+10\geq 0$
Nota: El signo desigualdad fue cambiado, ya que multiplicamos por un signo negativo.
Ahora, resolvemos la ecuación $latex 2x^-9x+10=0$:
$latex 2x^2-9x+10=0$
$latex (2x-5)(x-2)=0$
$latex x=\frac{5}{2}~~$ o $latex ~~x=2$
La desigualdad $latex 2x^2-9x+10\geq 0$ indica que necesitamos los valores de x que producen valores mayores o iguales a 0. Entonces, buscamos la porción de la parábola encima del eje x.
La solución es $latex x\leq 2~~$ o $latex ~~x\geq \frac{5}{2}$.
EJERCICIO 9
Resuelve la desigualdad $latex \frac{2}{x-3}\leq 1$.
Solución
Vamos a multiplicar a toda la desigualdad por $latex (x-3)^2$ para eliminar la fracción y asegurarnos de que la desigualdad sea positiva
$latex 2(x-3)\leq 1(x-3)^2$
$latex 2x-6\leq x^2-6x+9$
$latex 0\leq x^2-8x+15$
$latex x^2-8x+15\geq 0$
Resolvemos la ecuación $latex x^2-8x+15=0$ por factorización:
$latex x^2-8x+15=0$
$latex (x-5)(x-3)=0$
$latex x=5~~$ o $latex ~~x=3$
Ahora, tenemos que encontrar los valores de x que producen valores mayores que o iguales a 0.
Dado que la parábola se abre hacia arriba, la solución es $latex x\leq 3~$ o $latex ~x\geq 5$.
EJERCICIO 10
Resuelve la desigualdad $latex \frac{x+1}{7x-1}\leq \frac{2}{7}$.
Solución
Podemos multiplicar a toda la desigualdad por $latex (7x-1)^2$ para eliminar la fracción y asegurarnos de que la desigualdad sea positiva
$latex (x+1)(7x-1)\leq \frac{2}{7}(7x-1)^2$
$latex 7x^2+6x-1\leq \frac{2}{7}(49x^2-14x+1)$
$latex 0\leq 7x^2-10x+\frac{9}{7}$
$latex 49x^2-70x+9\geq 0$
Ahora, formamos la ecuación $latex 49x^2-70x+9=0$ y resolvemos por factorización:
$latex 49x^2-70x+9=0$
$latex (7x-1)(7x-9)=0$
$latex x=\frac{1}{7}~~$ o $latex ~~x=\frac{9}{7}$
Para resolver la desigualdad $latex 49x^2-70x+9\geq 0$, tenemos que encontrar los valores de x que producen valores mayores que o iguales a 0.
Dado que la parábola se abre hacia arriba, la solución es $latex x\leq \frac{1}{7}~$ o $latex ~x\geq \frac{9}{7}$.
5 Ejercicios de desigualdades cuadráticas para resolver
Resuelve los siguientes ejercicios para poner a prueba tu conocimiento de las desigualdades cuadráticas. Usa los ejercicios resueltos de arriba como guía.
Véase también
¿Interesado en aprender más sobre desigualdades? Puedes mirar estas páginas: