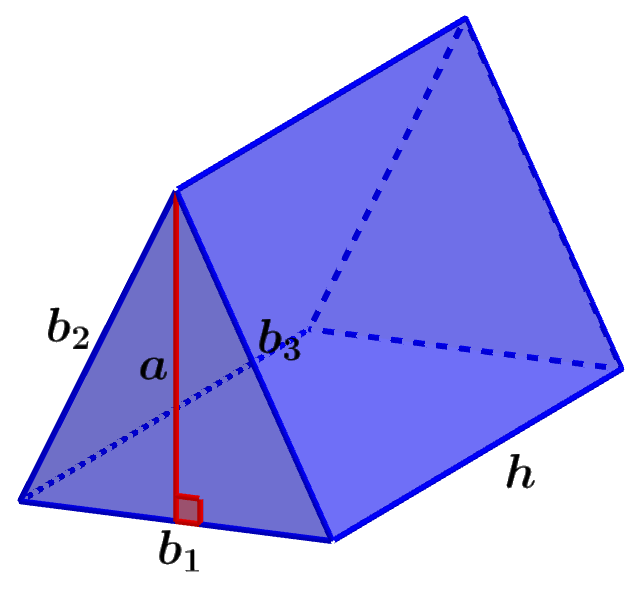
Un prisma triangular es una figura geométrica tridimensional. Estos prismas son poliedros formados de dos bases triangulares y tres caras rectangulares laterales. Similar a otros prismas, las dos bases son paralelas y congruentes la una con la otra. Los prismas triangulares tienen 5 caras, 6 vértices y 9 aristas. Las aristas y los vértices están unidos los unos con los otros a través de tres rectángulos laterales. Estos prismas son pentaedros que tienen nueve redes geométricas distintas.
A continuación, conoceremos más características de los prismas triangulares y usaremos diagramas para ilustrar los conceptos.
GEOMETRÍA
Relevante para…
Conocer las características fundamentales de los prismas triangulares.
GEOMETRÍA
Relevante para…
Conocer las características fundamentales de los prismas triangulares.
Definición de un prisma triangular
Un prisma triangular es un tipo de prisma que tiene dos bases y tres caras laterales. Los lados laterales tienen una forma rectangular y las bases tienen una forma triangular. En total, estos prismas tienen cinco caras, nueve vértices y seis aristas.
Las caras laterales y las bases del prisma triangular pueden o no ser congruentes dependiendo en si la base es un triángulo equilátero. Las aristas del prisma unen a las caras laterales correspondientes. Las aristas de los triángulos son paralelas la una con la otra.
Características principales de un prisma triangular
Las siguientes son algunas de las características más importantes de los prismas triangulares:
- Tienen un total de 9 aristas.
- Tienen un total de 5 caras.
- Tienen un total de 6 vértices.
- Tienen dos caras triangulares, llamadas bases y tres caras rectangulares, llamadas caras laterales.
- Las bases son paralelas y congruentes la una con la otra.
- Si es que las bases son triángulos equiláteros, las caras laterales son iguales la una con la otra.
Fórmulas importantes de prismas triangulares
Los prismas triangulares son figuras tridimensionales, por lo que sus propiedades más importantes son el volumen y el área superficial.
Fórmula del volumen
El volumen de un prisma es encontrado al multiplicar al área de su base por la longitud de su altura. Las bases son triangulares y sabemos que el área de cualquier triángulo es igual a un medio de la base multiplicada por la altura del triángulo. Entonces, tenemos la fórmula:
| $latex V=\frac{1}{2}bah$ |
en donde, b representa a la longitud de la base del triángulo, a representa a la altura del triángulo y h representa a la altura del prisma.
Fórmula del área superficial
Podemos encontrar el área superficial al sumar las áreas de todas las caras del prisma. Tenemos dos caras triangulares que son iguales, por lo que el área de ambas caras es ba. El área de las caras laterales es igual a la longitud del rectángulo por su altura.
Si es que tenemos un prisma con una base de triángulo equilátero, el área superficial es:
| $latex A_{s}=ba+3bh$ |
en donde, a representa a la altura del triángulo, b representa a la base o uno de los lados del triángulo y h representa a la altura del prisma.
Ejercicios de prismas rectangulares resueltos
Los siguientes ejercicios son resueltos aplicando las fórmulas de prismas rectangulares vistas arriba.
EJERCICIO 1
Un prisma triangular tiene una base de longitud 6 m y una altura de 5 m. Si es que la altura del prisma es 7 m, ¿cuál es el volumen del prisma?
Solución: De la pregunta, tenemos los valores $latex b=6$, $latex a=5$ y $latex h=7$. Entonces, usamos estos valores en la fórmula del volumen:
$latex V=\frac{1}{2}bah$
$latex V=\frac{1}{2}(6)(5)(7)$
$latex V=105$
El volumen del prisma es 105 m³.
EJERCICIO 2
Si es que un prisma tiene una base triangular de base 8 m y altura 6 m, ¿cuál es su volumen con una altura de 10 m?
Solución: Reemplazamos los valores dados en la fórmula del volumen:
$latex V=\frac{1}{2}bah$
$latex V=\frac{1}{2}(8)(6)(10)$
$latex V=240$
El volumen del prisma triangular es 240 m³.
EJERCICIO 3
Un prisma tiene una base que es un triángulo equilátero con lados de longitud 6 m y una altura de 5.2 m. Si es que la altura del prisma es 10 m, ¿cuál es su área superficial?
Solución: Tenemos los valores $latex b=6$, $latex a=5.2$ y $latex h=10$, por lo que usamos estos valores en la fórmula del área superficial:
$latex A_{s}=ba+3bh$
$latex A_{s}=(6)(5.2)+3(6)(10)$
$latex A_{s}=31.2+180$
$latex A_{s}=211.2$
El área superficial es 211.2 m².
EJERCICIO 4
¿Cuál es el área superficial de un prisma que tiene una altura de 9 m y una base triangular con lados de longitud 12 m y altura de 10.4 m?
Solución: Tenemos las longitudes $latex h=9$, $latex b=12$ y $latex a=10.4$. Al usar a estos valores en la fórmula del volumen, tenemos:
$latex A_{s}=ba+3bh$
$latex A_{s}=(12)(10.4)+3(12)(9)$
$latex A_{s}=124.8+324$
$latex A_{s}=448.8$
El área superficial es 448.8 m².
Véase también
¿Interesado en aprender más sobre prismas triangulares? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
