El área superficial de un prisma triangular es la superficie total cubierta por el prisma. El área superficial es una medida bidimensional, por lo que podemos usar m², cm² u otros. Para calcular el área superficial de cualquier figura 3D, tenemos que sumar las medidas de las áreas de todas las caras de la figura. Un prisma triangular tiene dos caras triangulares iguales y tres caras rectangulares.
A continuación, conoceremos la fórmula que podemos usar para calcular el área superficial de un prisma rectangular. Además, usaremos esta fórmula para resolver algunos ejercicios de práctica.
GEOMETRÍA
Relevante para…
Aprender a calcular el área superficial de prismas triangulares.
GEOMETRÍA
Relevante para…
Aprender a calcular el área superficial de prismas triangulares.
Fórmula del área superficial de un prisma triangular
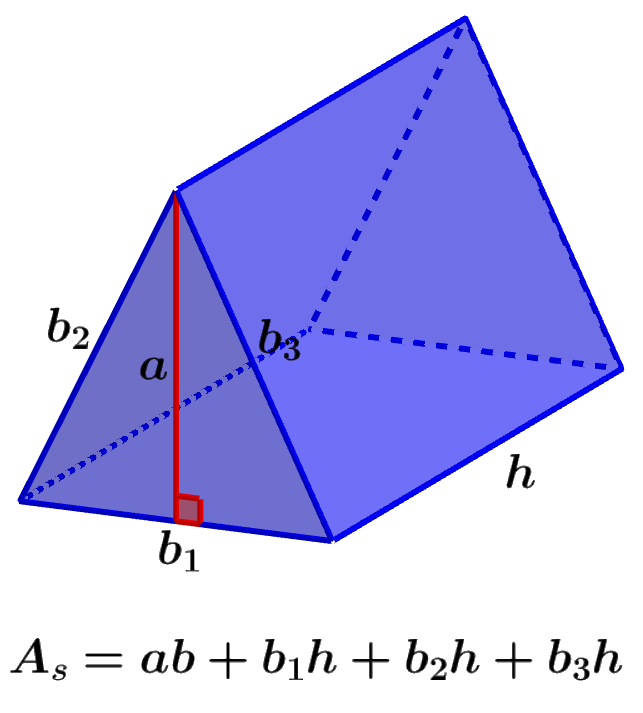
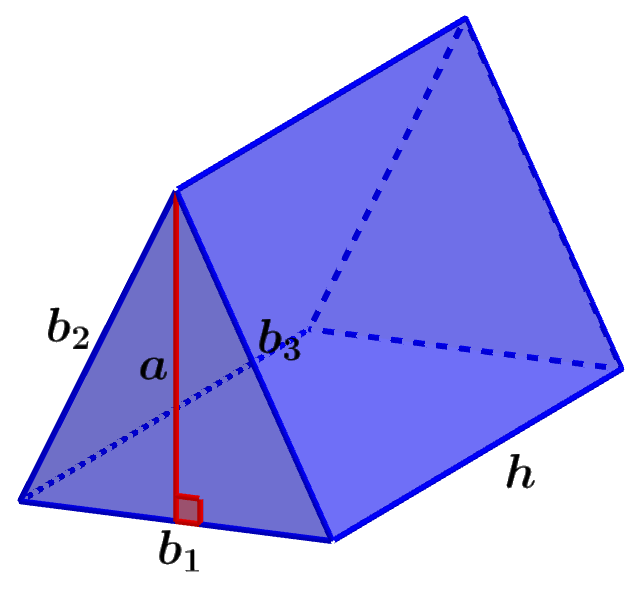
La fórmula del área superficial de un prisma triangular es obtenida al sumar las expresiones para las áreas de todas las caras del prisma. En un prisma triangular, tenemos dos caras triangulares iguales y tres caras rectangulares que pueden o no ser iguales.
Cada cara triangular tiene un área de $latex \frac{1}{2}ab$, en donde a es la longitud de la altura de la base triangular y b es la longitud de su base. Esto significa que el área de ambas caras triangulares es $latex ab$.
El área de cada cara rectangular es igual a la altura del prisma multiplicada por los tres lados de la base triangular. Es decir, tenemos las áreas $latex b_{1}h$, $latex b_{2}h$ y $latex b_{3}h$, en donde, $latex b_{1},~b_{2},~b_{3}$ son las longitudes de los lados de la base triangular y h es la longitud de la altura del prisma.
Entonces, al sumar todas estas áreas, tenemos:
| $latex A_{s}=ab+b_{1}h+b_{2}h+b_{3}h$ |
En el caso que la base sea un triángulo equilátero, sabemos que los tres lados del triángulo son iguales, por lo que las tres áreas de las caras laterales son iguales.
Ejercicios de área superficial de prismas triangulares resueltos
Los siguientes ejercicios son usados para practicar el uso de la fórmula del área superficial de prismas triangulares. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Un prisma triangular tiene una altura de 6 m y su base triangular tiene lados de longitud 5 m, 6 m, 5 m y una altura de 4 m. ¿Cuál es su área superficial?
Solución
Podemos obtener la siguiente información:
- Altura prisma, $latex h=6$
- Lado 1, $latex b_{1}=5$
- Lado 2, $latex b_{2}=6$
- Lado 3, $latex b_{3}=5$
- Altura triángulo, $latex a=4$
Usamos la fórmula del área superficial y sustituimos los valores dados:
$latex A_{s}=ab+b_{1}h+b_{2}h+b_{3}h$
$$A_{s}=(4)(6)+(5)(6)+(6)(6)+(5)(6)$$
$latex A_{s}=24+30+36+30$
$latex A_{s}=120$
El área superficial es 120 m².
EJERCICIO 2
Un prisma triangular tiene una altura de 10 m y su base triangular tiene lados de longitud 13 m, 10 m, 13 m y una altura de 12 m. ¿Cuál es su área superficial?
Solución
Tenemos los siguientes valores:
- Altura prisma, $latex h=10$
- Lado 1, $latex b_{1}=13$
- Lado 2, $latex b_{2}=10$
- Lado 3, $latex b_{3}=13$
- Altura triángulo, $latex a=12$
Usamos estos valores en la fórmula del área superficial y tenemos:
$latex A_{s}=ab+b_{1}h+b_{2}h+b_{3}h$
$$A_{s}=(12)(10)+(13)(10)+(10)(10)+(13)(10)$$
$latex A_{s}=120+130+100+130$
$latex A_{s}=480$
El área superficial es 480 m².
EJERCICIO 3
Tenemos un prisma triangular que tiene una base equilátera de lados 6 m y una altura de 5.2 m. Si es que la altura del prisma es 5 m, ¿cuál es su área superficial?
Solución
En este caso, tenemos un triángulo equilátero, por lo que sabemos que los lados del triángulo son iguales. Entonces, tenemos:
- Altura prisma, $latex h=5$
- Lado, $latex b=6$
- Altura triángulo, $latex a=5.2$
Usamos la fórmula del área superficial con estos datos y combinamos las tres áreas de los lados laterales ya que son iguales:
$latex A_{s}=ab+bh+bh+bh$
$latex A_{s}=ab+3bh$
$latex A_{s}=(5.2)(6)+3(6)(5)$
$latex A_{s}=31.2+90$
$latex A_{s}=121.2$
El área superficial es 121.2 m².
EJERCICIO 4
Un prisma tiene una base que es un triángulo equilátero con lados de longitud 9 m y una altura de 7.8 m. Si es que la altura del prisma es 8 m, ¿cuál es su área superficial?
Solución
Tenemos la siguiente información:
- Altura prisma, $latex h=8$
- Lado, $latex b=9$
- Altura triángulo, $latex a=7.8$
Usamos la fórmula del área superficial y sustituimos los valores dados:
$latex A_{s}=ab+b_{1}h+b_{2}h+b_{3}h$
$latex A_{s}=ab+3bh$
$latex A_{s}=(7.8)(9)+3(9)(8)$
$latex A_{s}=70.2+216$
$latex A_{s}=286.2$
El área superficial es 286.2 m².
Ejercicios de área superficial de prismas triangulares para resolver
Pon en práctica el uso del área superficial de prismas triangulares para resolver los siguientes ejercicios. Selecciona una respuesta y verifícala para comprobar que seleccionaste la correcta. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre prismas triangulares? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
