El heptágono es un polígono que tiene siete lados y siete ángulos internos. La suma de todos los ángulos internos de un heptágono es igual a 900°. Dependiendo en las características que tomemos, podemos distinguir a diferentes tipos de heptágonos. Por ejemplo, si es que consideramos la longitud de los lados y la medida de los ángulos, podemos identificar a heptágonos regulares e irregulares. Si es que consideramos al contorno, podemos identificar a heptágonos convexos y cóncavos.
A continuación, veremos una breve definición de los heptágonos y conoceremos algunos tipos de heptágonos. Además, descubriremos algunas de las características fundamentales de estas figuras geométricas. Finalmente, aprenderemos las fórmulas más importantes de los heptágonos regulares y las usaremos para resolver algunos ejercicios.
GEOMETRÍA
Relevante para…
Conocer las características fundamentales de los heptágonos.
GEOMETRÍA
Relevante para…
Conocer las características fundamentales de los heptágonos.
Definición de un heptágono
Podemos definir a un heptágono como un polígono de siete lados y siete ángulos internos. Por su parte, un polígono es una figura cerrada bidimensional formada de segmentos rectos.
El heptágono es formado por todos sus lados, los cuales se encuentran el uno con el otro extremo a extremo. Dependiendo en diferentes características, podemos distinguir a los siguientes tipos de heptágonos:
- Regulares e irregulares
- Convexos y cóncavos
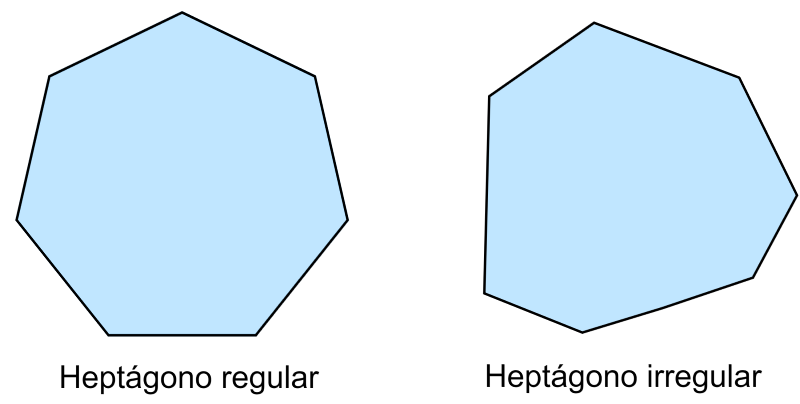
Heptágonos irregulares y regulares
Los heptágonos regulares tienen la característica de tener lados con la misma longitud y ángulos con la misma medida. Los heptágonos irregulares tienen la característica de tener lados de diferentes longitudes, ángulos de diferentes medidas o ambas al mismo tiempo.
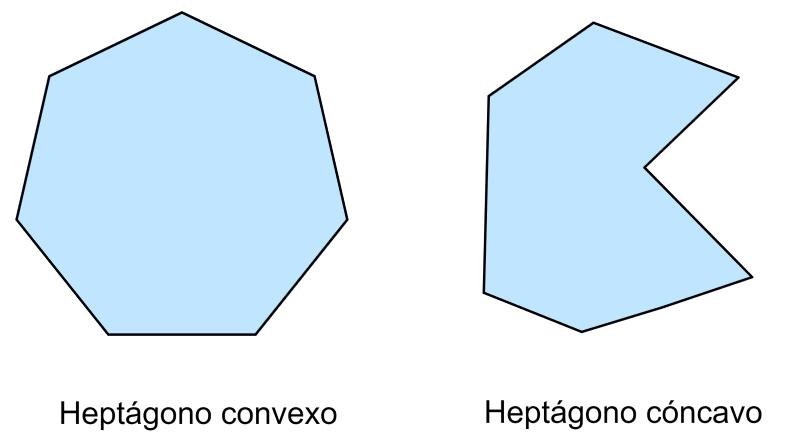
Heptágonos convexos y cóncavos
Los heptágonos convexos son polígonos que tienen todos sus vértices apuntando hacia afuera. Los heptágonos cóncavos son polígonos que tienen por lo menos un vértice que está apuntando hacia adentro.
Características fundamentales de un heptágono
Los heptágonos tienen las siguientes características fundamentales:
- En un heptágono, la suma de todos los ángulos internos es 900°.
- Un heptágono regular tiene siete lados de la misma longitud.
- Un heptágono regular tiene siete ángulos con la misma medida.
- La suma total de los ángulos internos es 360°
- Cada ángulo interno de un heptágono regular mide 128.57°.
- El número total de diagonales en un heptágono regular es 14.
- El número de triángulos formados en un heptágono es siete.
Fórmulas importantes de un heptágono
Las fórmulas más importantes de un heptágono son la fórmula del perímetro, del área y de la apotema.
Fórmula del perímetro de un heptágono regular
El perímetro es la suma de las longitudes de todos los lados de un heptágono. Dado que un heptágono regular tiene siete lados iguales, tenemos:
| $latex p=7l$ |
en donde, l es la longitud de uno de los lados del heptágono.
Fórmula del área de un heptágono regular
La fórmula del área de un heptágono es:
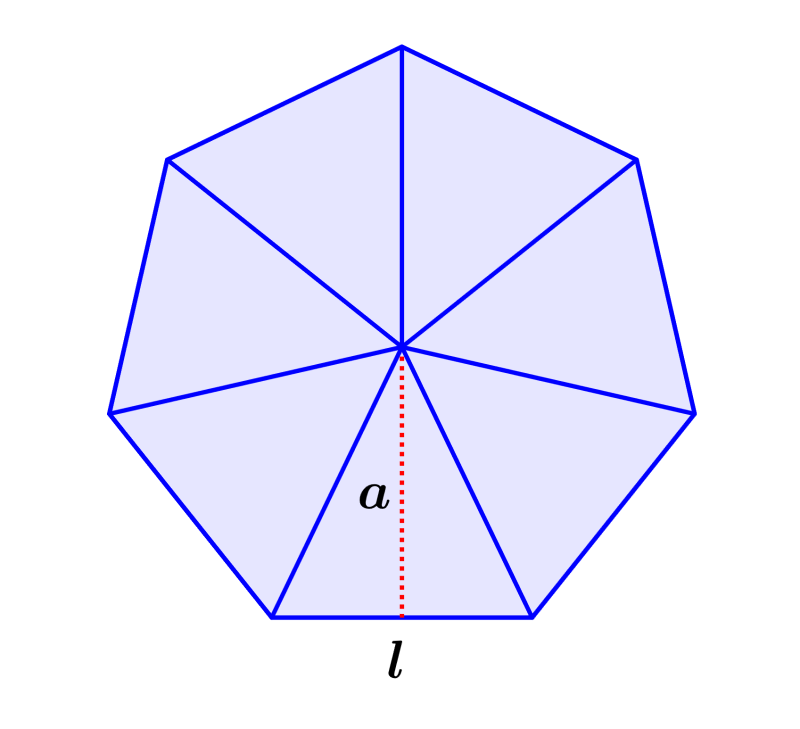
| $latex A= \frac{7}{2}la$ |
en donde, l es la longitud de los lados y a es la longitud de la apotema del heptágono.
Fórmula de la apotema de un heptágono regular
Podemos encontrar la apotema de un heptágono usando la siguiente fórmula:
| $latex a= \frac{l}{2tan(25.71°)}$ |
en donde, l es la longitud de un lado del heptágono.
Ejemplos de problemas de heptágonos
EJEMPLO 1
- ¿Cuál es el perímetro de un heptágono con lados de longitud 13 m?
Solución: Usamos $latex l=13$ en la fórmula del perímetro:
$latex p=7l$
$latex p=7(13)$
$latex p=91$
El perímetro es 91 m.
EJEMPLO 2
- ¿Cuál es el área de un heptágono que tiene lados de longitud 11 m y una apotema de 11.42 m?
Solución: Tenemos $latex l=11$ y $latex a=11.42$. Entonces, usamos estas longitudes en la fórmula del área:
$latex A= \frac{7}{2}la$
$latex A= \frac{7}{2}(11)(11.42)$
$latex A=439.67$
El área del heptágono es 439.67 m².
EJEMPLO 3
- ¿Cuál es la apotema de un heptágono que tiene lados de longitud 10 m?
Solución: Usamos la fórmula de la apotema con $latex l=10$:
$latex a= \frac{l}{2\tan(25.71)}$
$latex a= \frac{10}{2\tan(25.71)}$
$latex a=10.38$
La longitud de la apotema es 10.38 m.
Ejercicios de heptágonos para resolver
Véase también
¿Interesado en aprender más sobre heptágonos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
