El pentágono es una figura geométrica que tiene cinco lados y cinco ángulos. Los ángulos internos en un pentágono suman 540°. Dependiendo en las características que tomemos, podemos distinguir a algunos tipos de pentágonos. Podemos tener pentágonos regulares e irregulares y pentágonos convexos y cóncavos.
A continuación, miraremos una definición de los pentágonos y una descripción breve de los tipos de pentágonos. También, conoceremos algunas de las características más importantes de estas figuras geométricas. Además, haremos una revisión de sus fórmulas más importantes y las aplicaremos para resolver algunos ejercicios de pentágonos regulares.
GEOMETRÍA
Relevante para…
Conocer las características fundamentales de un pentágono.
GEOMETRÍA
Relevante para…
Conocer las características fundamentales de un pentágono.
Definición de un pentágono
Un pentágono es un polígono con 5 lados y 5 ángulos. La palabra “pentágono” está formada de dos partes, penta y gonia que significan cinco ángulos. Todos los lados del pentágono se encuentran el uno con el otro extremo a extremo para formar una figura.
Dependiendo de los lados, ángulos y vértices, existen diferentes tipos de pentágonos tales como:
- Regulares e irregulares
- Convexos y cóncavos
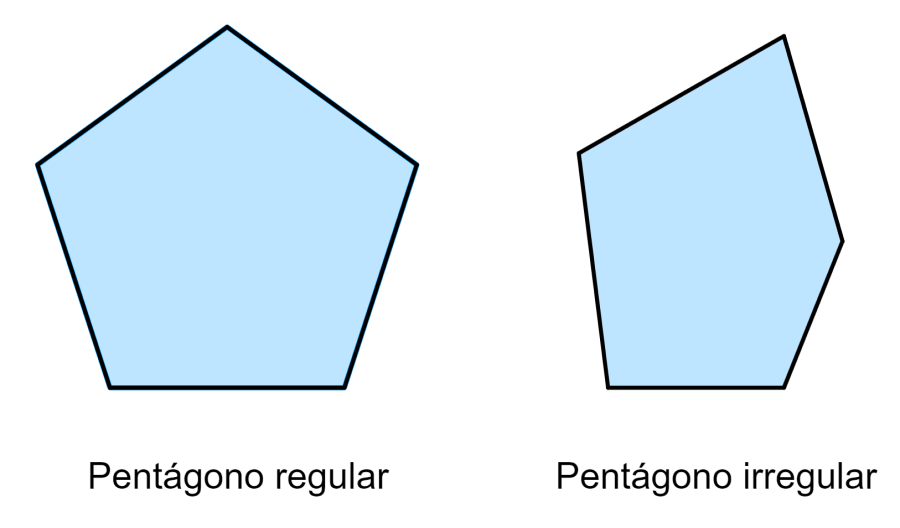
Pentágonos irregulares y regulares
Si es que un pentágono es regular, todos los lados tienen las mismas longitudes y los cinco ángulos tienen la misma medida. Si es que el pentágono no lados con iguales longitudes o ángulos con la misma medida, entonces, es un pentágono irregular.
Pentágonos convexos y cóncavos
Si es que todos los vértices de un pentágono están apuntando hacia afuera, el pentágono es convexo. Por otra parte, si es que el pentágono tiene por lo menos un vértice que está apuntando hacia adentro, entonces, el pentágono es cóncavo.
Características fundamentales de un pentágono
Las siguientes son algunas de las características más importantes de un pentágono:
- La suma de todos los ángulos internos es 540°.
- Un polígono regular tiene los cinco lados con la misma longitud.
- Un polígono regular tiene los cinco ángulos con la misma medida.
- En un polígono regular, cada ángulo interno mide 108° y cada ángulo exterior mide 72°.
Fórmulas importantes de un pentágono
Las fórmulas más importantes de los pentágonos son la fórmula del perímetro, la fórmula del área y la fórmula de la apotema.
Fórmula del perímetro de un pentágono
Dado que todos los lados del pentágono regular tienen la misma longitud, el perímetro de un pentágono es:
| $latex p=5l$ |
en donde, l es la longitud de los lados del pentágono.
Fórmula del área de un pentágono
Para un pentágono regular, el área está dada por:
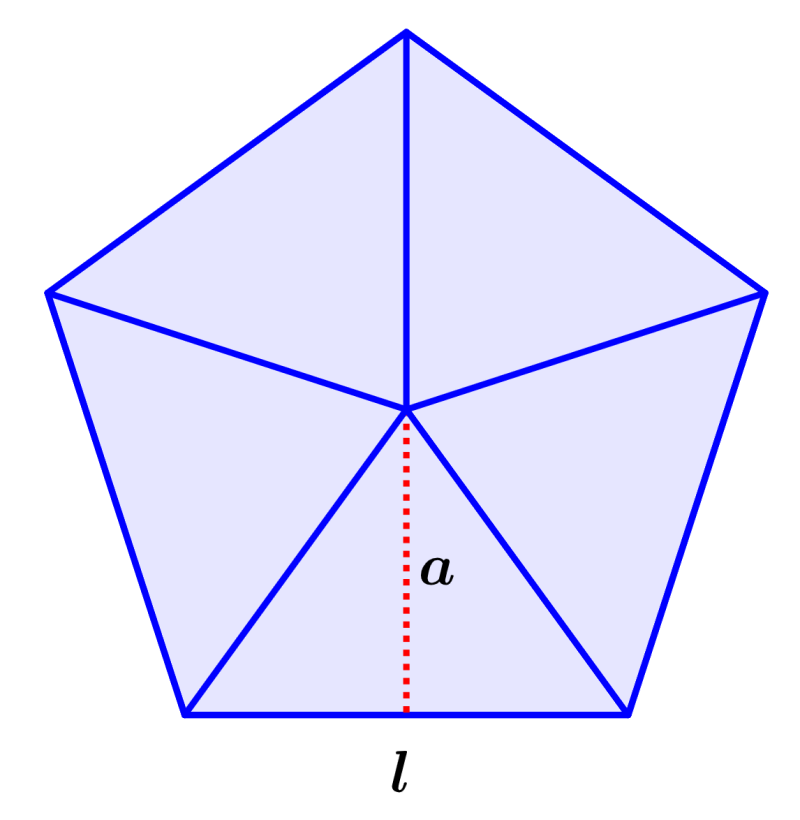
| $latex A= \frac{5}{2}la$ |
en donde, l es la longitud de los lados y a es la longitud de la apotema del pentágono.
Fórmula de la apotema de un pentágono
Un pentágono regular tiene la siguiente apotema:
| $latex a= \frac{l}{2\tan(36°)}$ |
en donde, l es la longitud de un lado del pentágono.
Ejemplos de problemas de pentágonos
EJEMPLO 1
- ¿Cuál es el perímetro de un pentágono que tiene lados de longitud 23 m?
Solución: Usamos la fórmula del perímetro con $latex l=23$:
$latex p=5l$
$latex p=5(23)$
$latex p=115$
El perímetro es 115 m.
EJEMPLO 2
- ¿Cuál es el área de un pentágono que tiene lados de longitud 10 m y una apotema de longitud 6.88 m?
Solución: Usamos la fórmula del área con $latex l=10$ y $latex a=6.88$:
$latex A= \frac{5}{2}la$
$latex A= \frac{5}{2}(10)(6.88)$
$latex A=172$
El área del pentágono es 172 m².
EJEMPLO 3
- ¿Cuál es la apotema de un pentágono que tiene lados de longitud 8m?
Solución: Usamos la fórmula de la apotema con $latex l=8$:
$latex a= \frac{l}{2\tan(36°)}$
$latex a= \frac{8}{2\tan(36°)}$
$latex a= \frac{8}{1.453}$
$latex a=5.5$
La longitud de la apotema es 5.5 m.
Ejercicios de pentágonos para resolver
Véase también
¿Interesado en aprender más sobre pentágonos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
